第十三次作业

作业

---

一、背景

关于波动，我们有波动方程：

$$\frac{\partial^2 y}{\partial t^2}=c^{2}\frac{\partial^2 y}{\partial x^2}$$
正文
习题6.6
齐次线性偏微分方程的一个重要特征是有限个解的线性组合也是方程的解。由此，在弦上运动的两个波包的运动是独立的。为了说明这一点，我们在弦上的x=0.3m，0.7m处各施加一个峰值不同的高斯型扰动，观察之后波包的运动。
代码：

import division
from matplotlib import animation
import matplotlib.pyplot as plt
import numpy as np
from copy import deepcopy
fig = plt.figure()
ax = fig.add_subplot(1,1,1,xlim=(0,1),ylim=(-1,1))
line, = ax.plot([],[],lw=2)
def init():
    x = np.linspace(0,1,101)
    y = np.exp(-1000*(x-0.3)**2) + 0.5*np.exp(-1000*(x-0.7)**2) 
    y[0] = 0
    y[-1] = 0
    line.set_data(x,y)
    return line,
def iteration(num):
    x = np.linspace(0,1,101)
    y_now = np.exp(-1000*(x-0.3)**2) + 0.5*np.exp(-1000*(x-0.7)**2)
    y_now[0] = 0
    y_now[-1] = 0
    y_before = deepcopy(y_now)
    y_after = np.zeros(101)
    for j in range(num):
        for i in range(101):
            if i== 0 or i== 100:
                y_after[i] = 0
            else:
                y_after[i] = - y_before[i] + y_now[i+1] + y_now[i-1]
        y_before = deepcopy(y_now)
        y_now = deepcopy(y_after)
    return y_now
def animate(i):
    x = np.linspace(0,1,101)
    y = iteration(i)
    line.set_data(x,y)
    return line,
anim1=animation.FuncAnimation(fig, animate, init_func=init, frames=200, interval=5)
plt.xlabel('x(m)')
plt.ylabel('y(m)')
plt.title('wave on a string')
plt.grid(True)
plt.show()

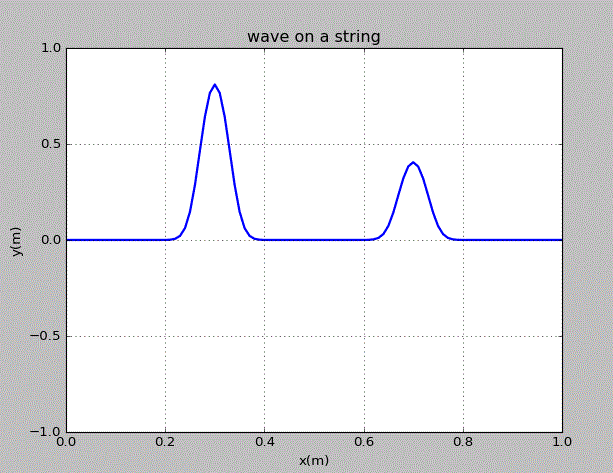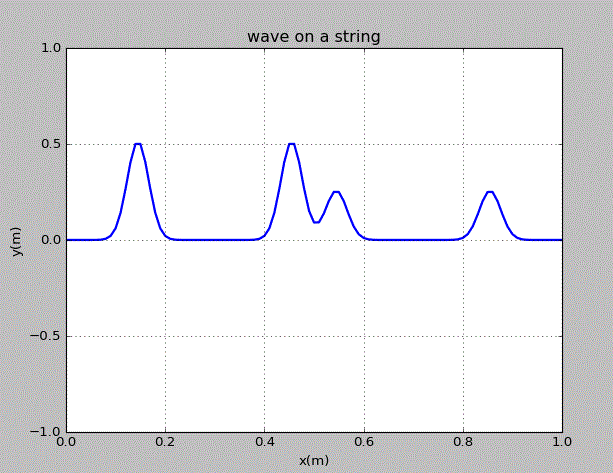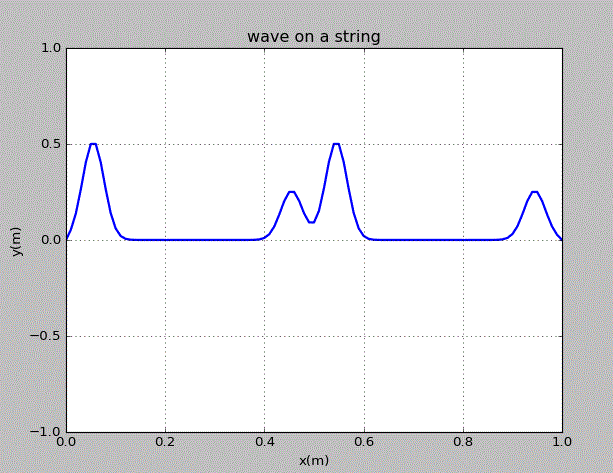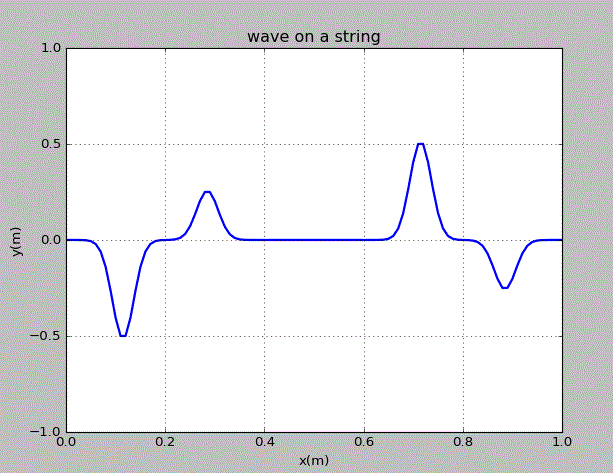
由图可知，各个波之间没有相互干扰，其在“碰撞”前后的形状和速度均没有变化。由此可知，这几个波作为弦的运动的解，是相互独立的。

初始波形不同时弦的振动情况
接下来我们考察当初始波形不同时弦上的波的传播情况。
当初始的波为x=0.4~0.6上的方波时,情况为：

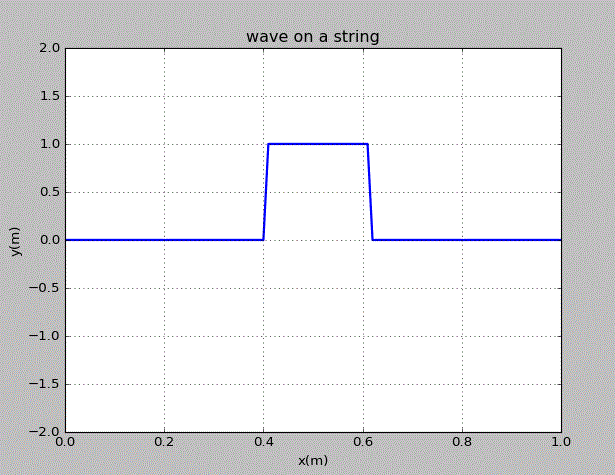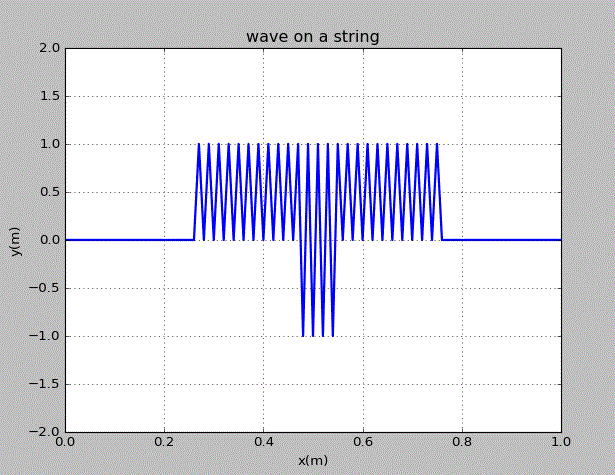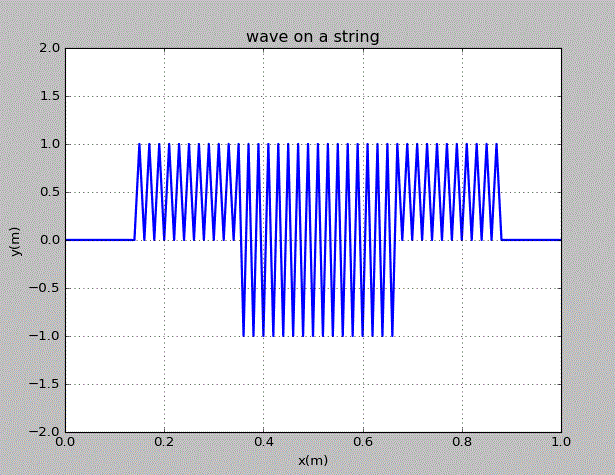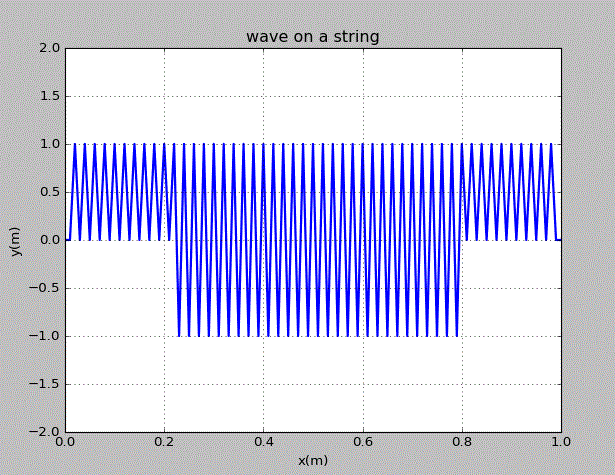
当初始的波为三角波时，情况为：

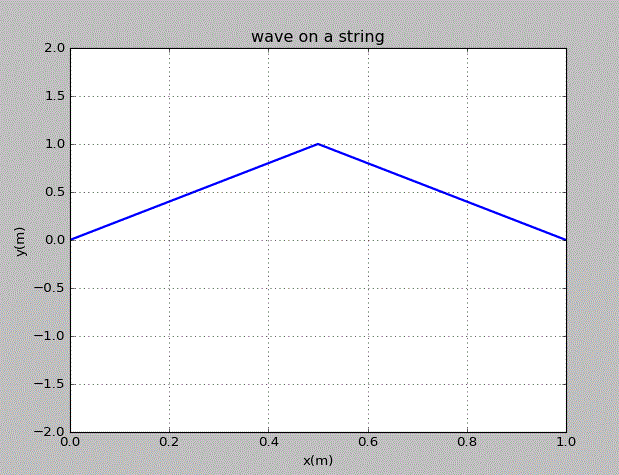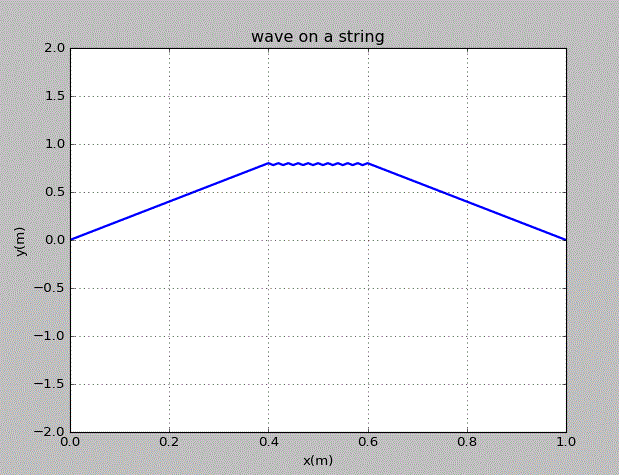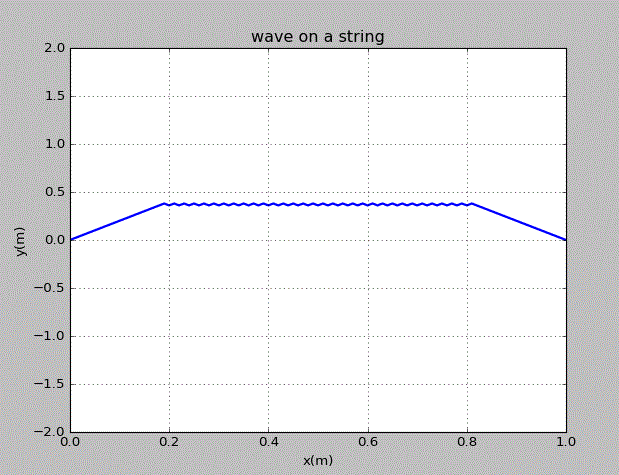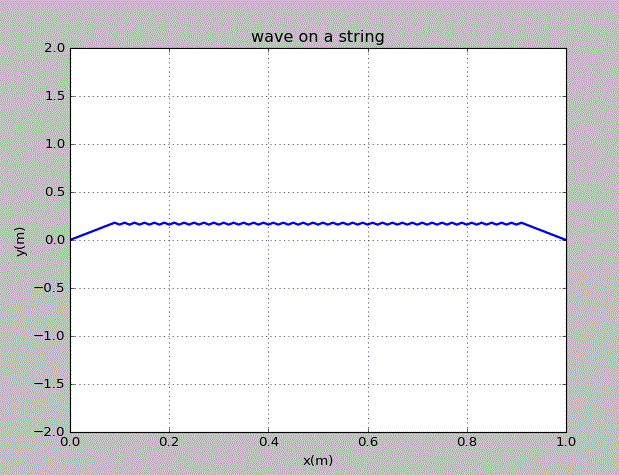
当初始的波为上半圆时，情况为：

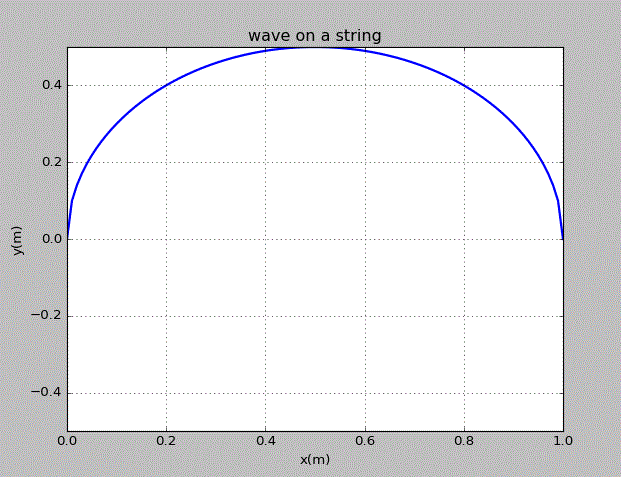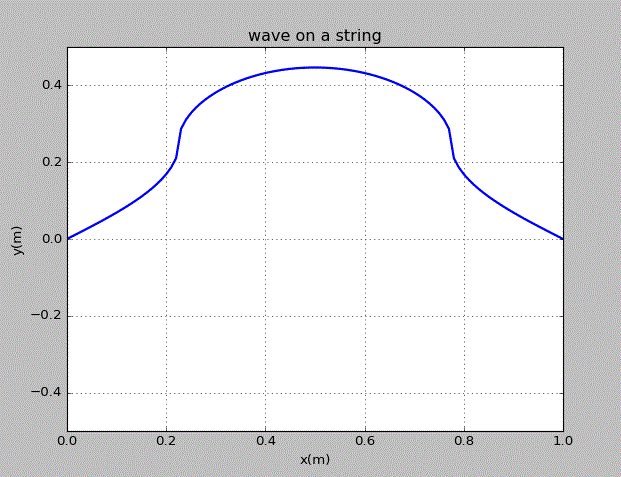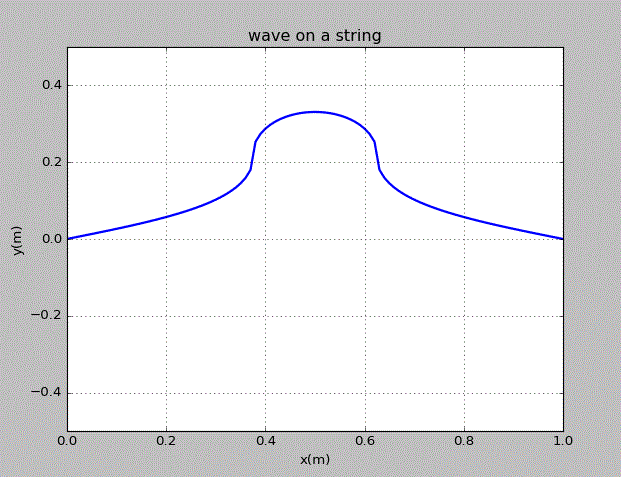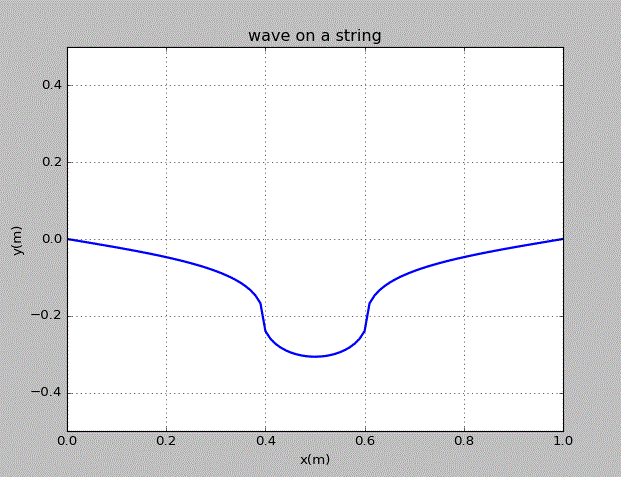
致谢
感谢《计算物理》第六章，感谢吴雨桥同学。