Work_7th chapter 3 NO 3.28

St: Wenya Wu 201530102016 WHU

3.28 Estimate qualitatively the Lyapunov exponent for a few trajectories of the Lorenz model near the transition to chaos at r=24.74....Try to observe this exponent change from negative in the nonchaotic regime, to positive in the chaotic regime.

综述

• Lorenz 模型方程：
  $$\frac{dx}{dt}=\sigma(y-x)$$ $$\frac{dy}{dt}=-xz+rx-y$$ $$\frac{dz}{dt}=xy-bz$$
  $x,y,z$分别表示流体的温度、密度、速度；$\sigma,r,b$与流体和其他流体的温度差有关.
• 设定不同的参数，计算出洛伦兹模型的解， 做出解的相图，观察其混沌的特性
• 观察逐渐过渡到混沌情形的相图
• 迭代计算李雅普诺夫常数，并分析其正负性及相应的馄钝性

公式说明

$$x_{i+1}=x_i+[\sigma(y_i-x_i)]dt$$ $$y_{i+1}=y_i-(x_iz_i-rx_i+y_i)dt$$ $$z_{i+1}=z_i+(x_iy_i-bz_i)dt$$

计算过程及结果

• 设定$\sigma=10,r=5，10，25,b=2.67$画出$z-t$图像（初始条件均为$x=1,y=z=0$）代码
  
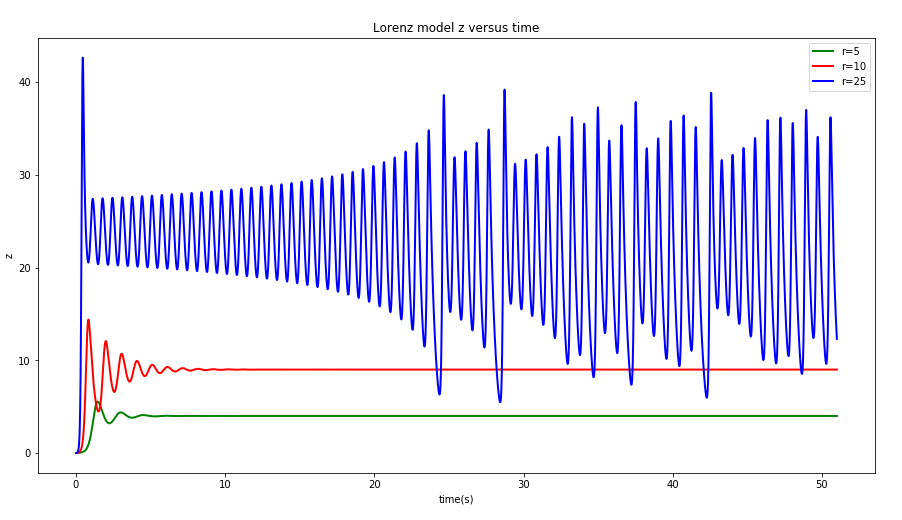
  相应的z-x相图：
  
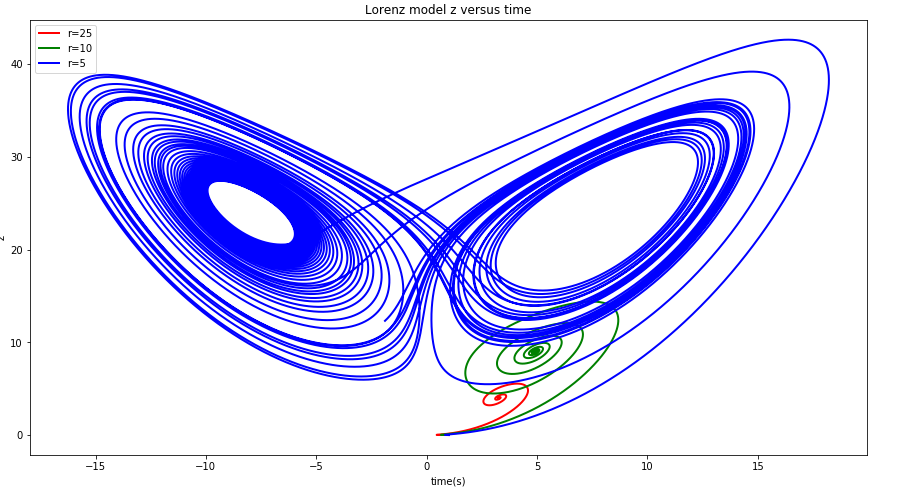
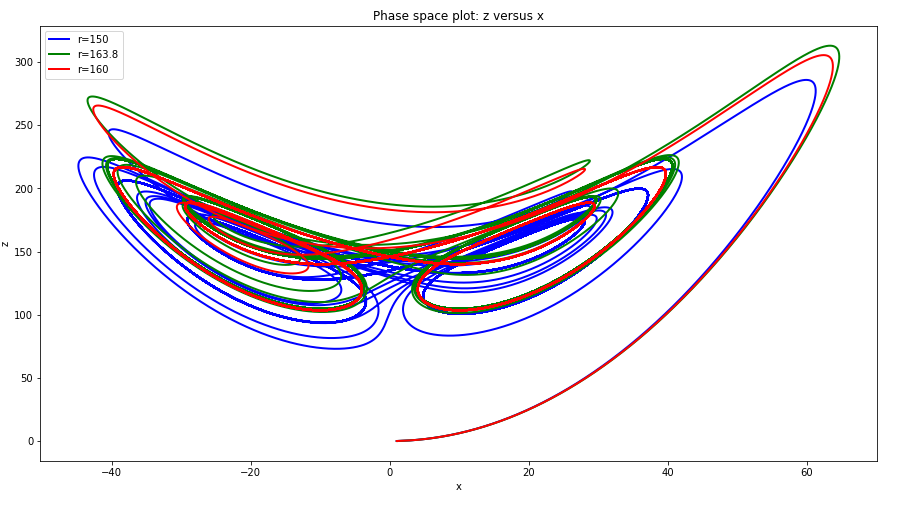
  增大r=150,160,163.8后：
  
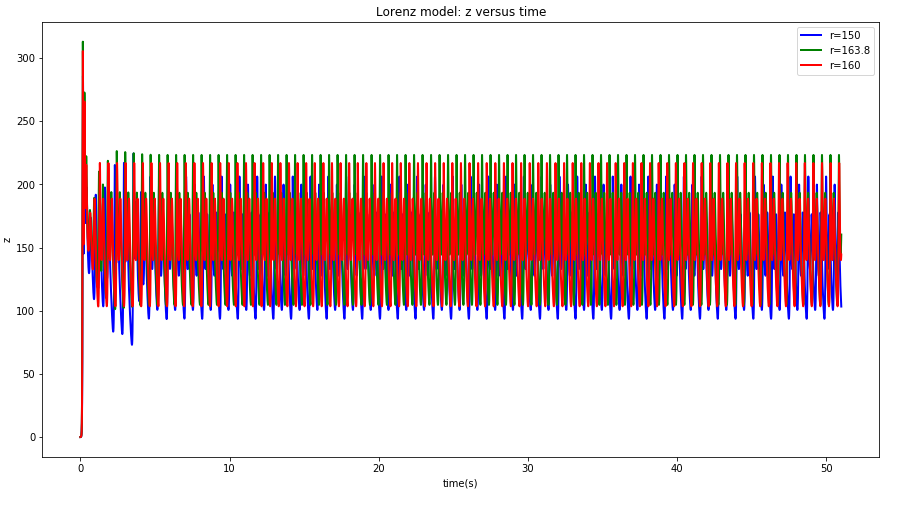
  相应的z-x相图：
  
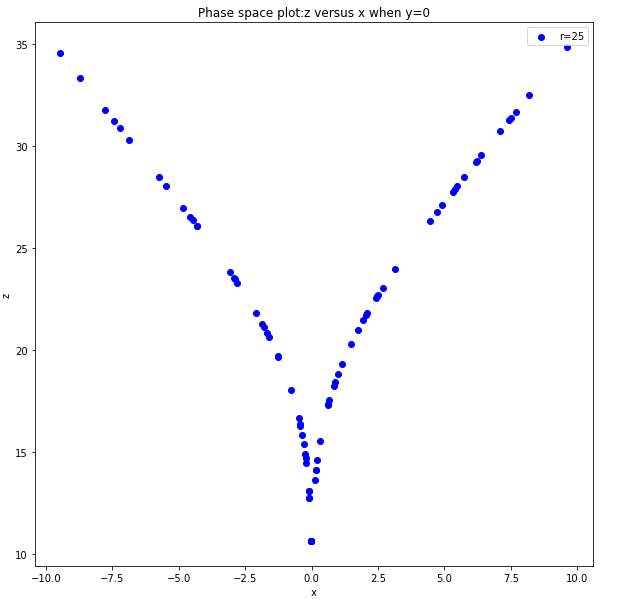
• 当r=25时做出z-y,z-x相图（仅取t=30s以后的点）代码
  
  
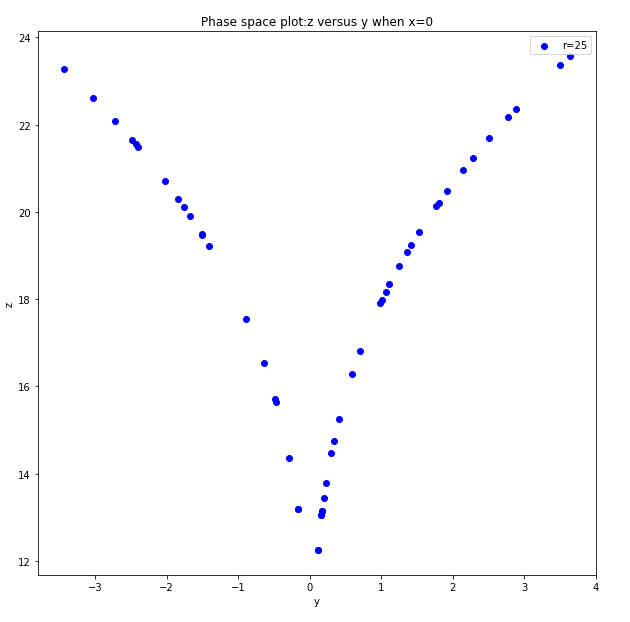
• 在接近混沌的r值附近改变r的大小，观察相图的变化
  
  
  
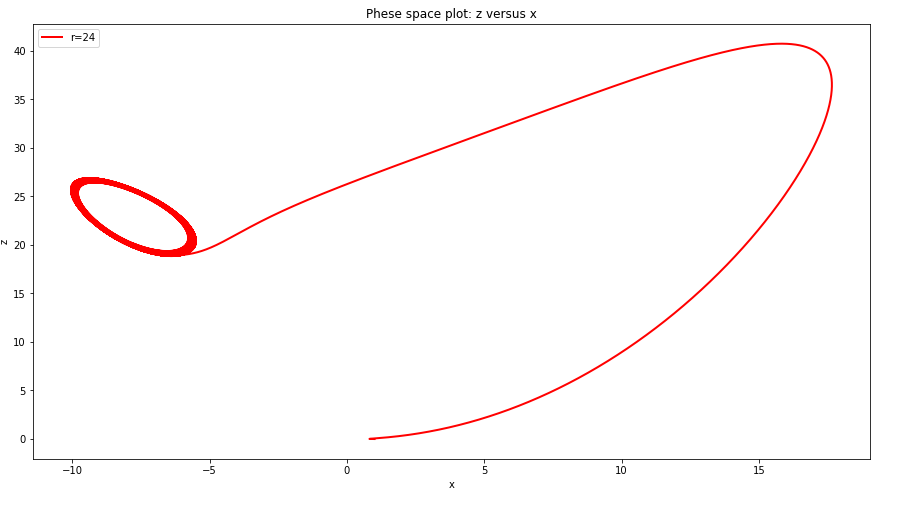
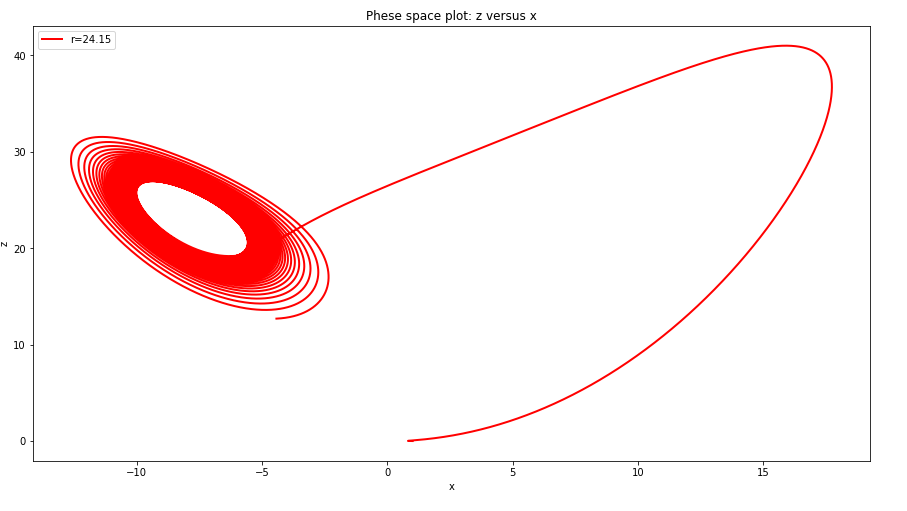
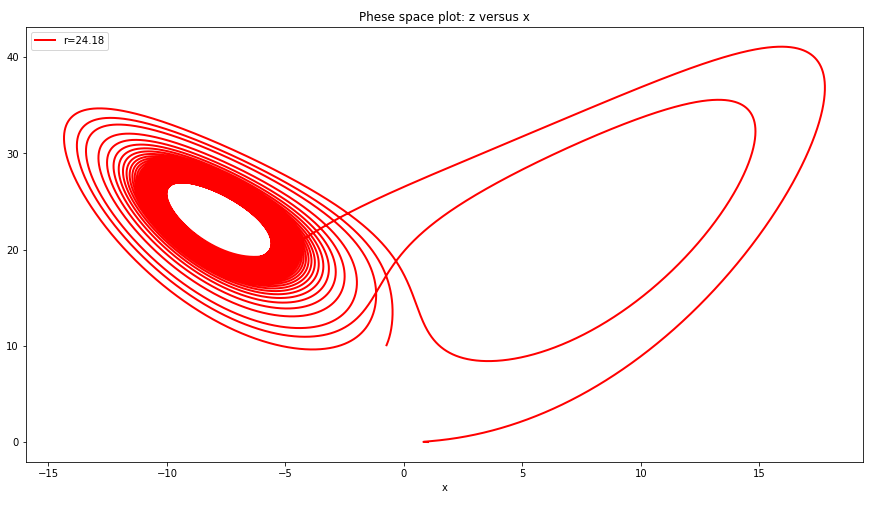
  从图中可以看出，在接近混沌的r值附近，当r小于“混沌点”时，没有双吸引子出现，相图仅局限于一个区域，当大于r的“混沌点”时，相图上的点跳出原来局域部分，形成双吸引子.r的“混沌点”在24.1左右.
• 计算lorenz 模型的李雅普诺夫特征指数.
  李雅普诺夫特征指数表征初始条件变化小量导在运行一段时间后的偏移值的发散情况，当$\lambda>0$时，运行一段时间后的偏移值发散，表示系统处于混沌状态；当$\lambda<0$时，偏移值并没有发散（因为$\lambda$在指数上），表示系统未处于混沌状态。
  利用定义式 $$\lambda=\frac{1}{n}ln\frac{\delta x_n}{\delta x_0}$$ 进行估计
  设定初始偏差为$\delta x_0=\delta y_0=\delta z_0=0.0001$
  计算程序代码
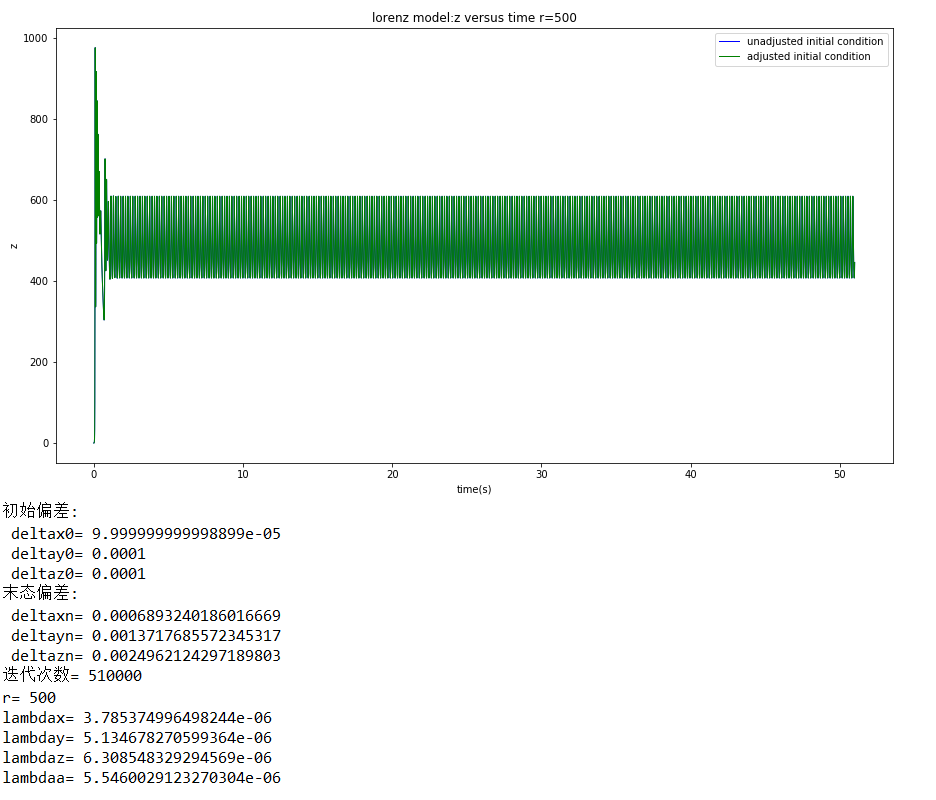
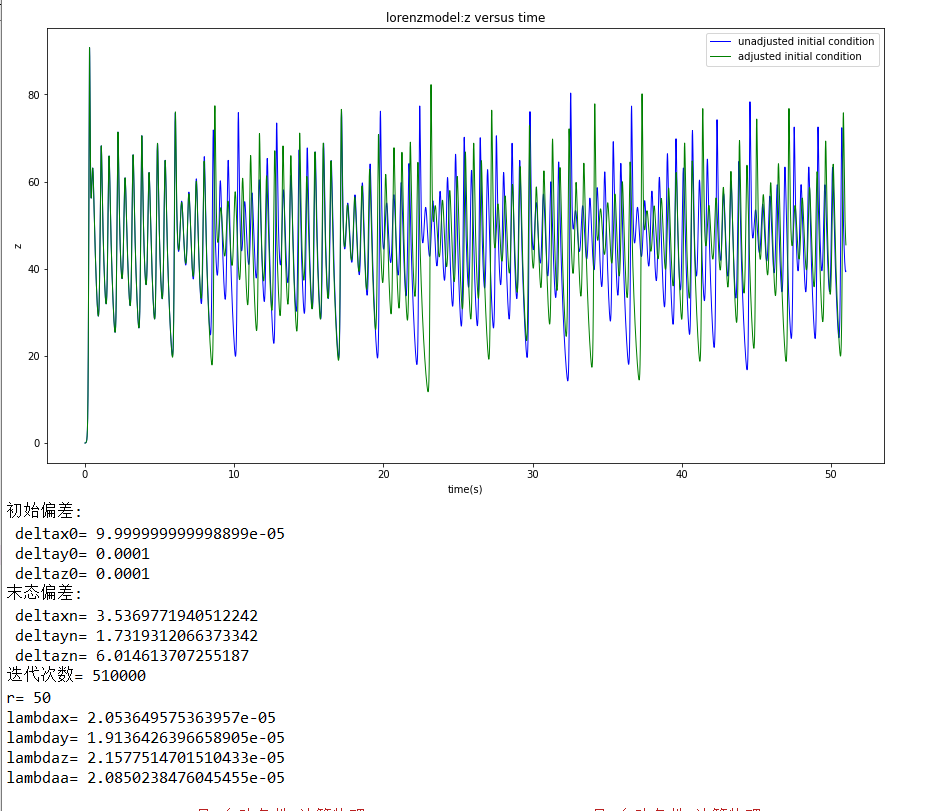
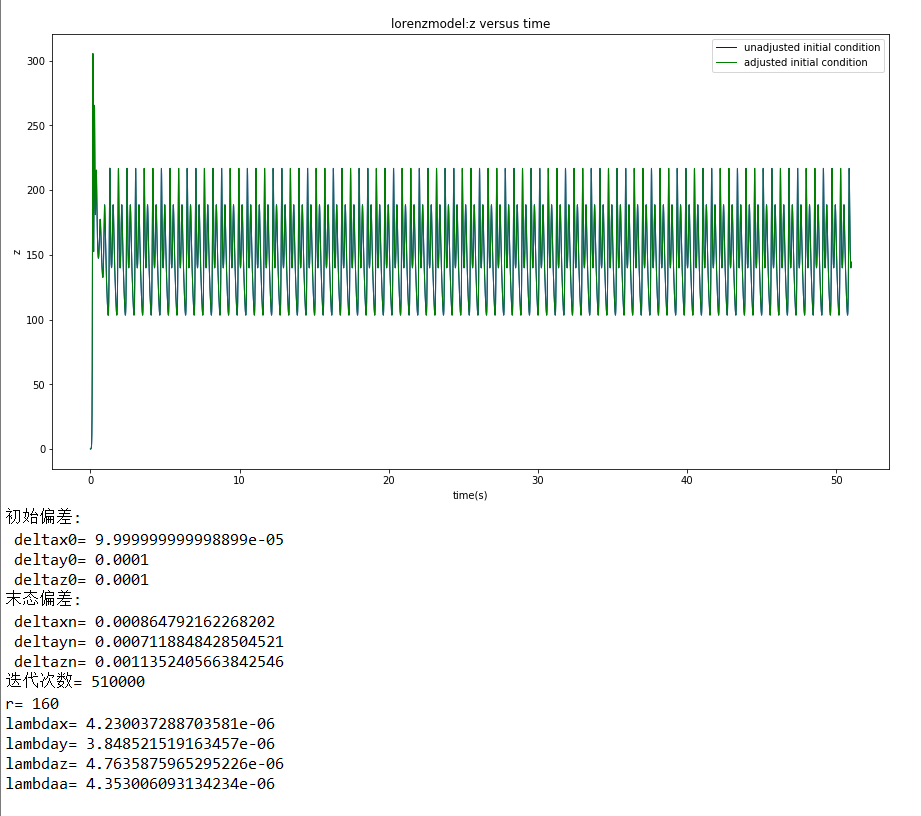
  运行结果：
  
  从上面的结果可以看出，四个$\lambda$均在r=23.85附近接近于0,可以判断“混沌的临界点”在r=23.85左右。
  改变初始条件，画图，观察具体的偏差，又可以得到一下的几个结论：
  1.发现实际进入混沌的“混沌临界点”并不是计算所得值（r=23.85）而是在r为24到24.3之间（同样的初始条件及其变化量），这是因为前面计算李雅普诺夫指数的方法只是估计值而并未解析的计算（见附录）
  
  
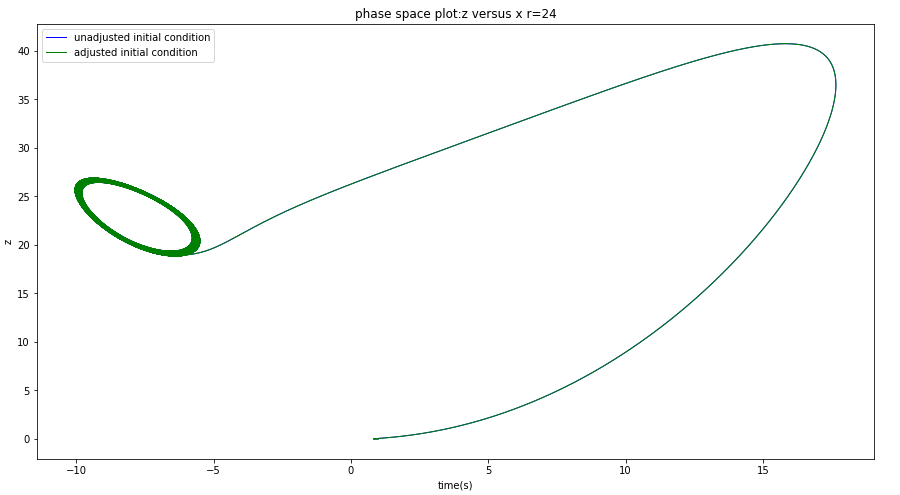
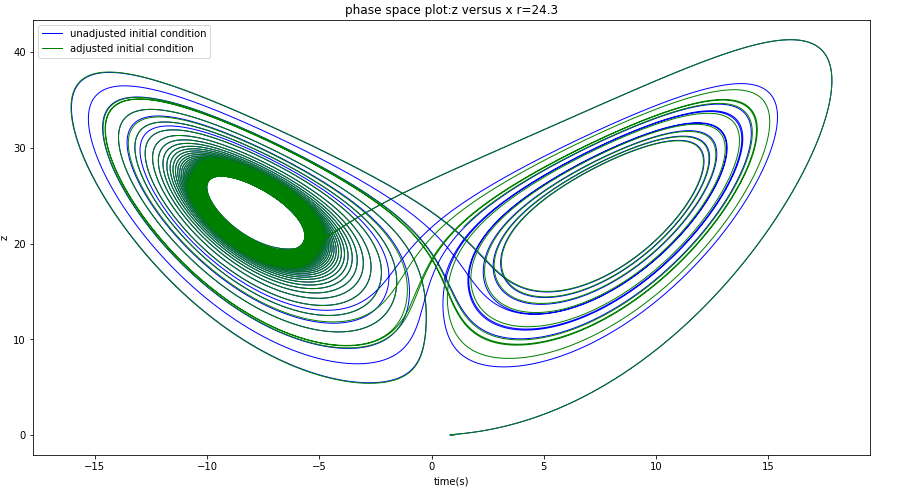
  2.发现当r=160的时候混沌又“几乎”消失了,再增大r，$\lambda$越来越趋近于0，但不会变成负值。所以混沌现象应该是在r=27左右最明显（多次改变r得到的结论），之后随着r增大，混沌依然存在，但越来越不明显。
  
  
  

附录

1.李雅普诺夫特征指数意义介绍：对于一维映射：$x_{n+1}=f(x_n)$,考虑初始值$x_0$与它的临近值$x_0+\delta x_0$，由上面的映射坐一次迭代，两点的距离变成：

$$\delta x_1=|f(x_0+\delta x_0)-f(x_0)|=\frac{df(x_0)}{dx}\delta x_0$$
经过n次迭代后，两点距离变成：
$$\delta x_n=|f^{(n)}(x_0+\delta x_0)-f^{(n)}(x_0)|=\frac{df^{(n)}(x_0)}{dx}\delta x_0=e^{\lambda n}\delta x_0$$
其中$\lambda$即为李雅普诺夫特征指数.
上面的式子要求系统的偏差随着迭代将以指数形式放大，这是混沌系统的重要特征之一.
2.李雅普诺夫指数的计算方法：

这是精确计算n次迭代后的指数的方法。
3.针对Lorenz模型的数值计算公式，有以下两个问题：
①由于lorenz模型是三维映射，所以应该有三个李雅普诺夫指数，同时，自变量变成三维向量，迭代的求导项变成雅可比矩阵(详见下图推导)


上面的式子表明，这样计算下来的李雅普诺夫指数实际上是包含了（δx,δy,δz）三个坐标的（因为有矢量的模），这区别于单独计算某个分量的李雅普诺夫指数。不过也可以用直接求比的方法计算单个分量的李雅普诺夫指数。于是，我们最应该计算出四个指数$\lambda_x,\lambda_y,\lambda_z,\lambda$。
②求解雅可比矩阵的本征值和本征矢计算量巨大（由于每次迭代数据值不同），可以考虑设置一个初始偏差（0.0001），用ｎ次迭代后的偏差和初始差值之比来“估计”n次迭代后的李雅普诺夫指数精确值。（所以这样计算下来的并不是精确值，初始的偏差越趋于0，计算结果越阶级精确值）

总结

本次作业重点研究了lorenz模型的李雅普诺夫常数，对相应问题进行了大量计算，得到了较为符合实际的结论。
混沌现象随着参数变化而变化，参数使得系统一旦进入混沌，很难再回到不混沌的状态。
参考资料：
《混沌及其应用》（作者：黄润生 武汉大学出版社）