Quantunm Mechanics —— How to Solving Methods of Schrodinger Equation?

St: 吴文雅
NO.201530102016

摘要

薛定谔方程是量子力学的基本方程之一，不同形式的薛定谔方程，具有精确的解析解的屈指可数，因此计算数值解的方法尤为重要。本文尝试了包括“shooting method、matching method、variational Monte Carlo”三种不同的求解方法，并对各种方法进行了具体的计算和评价。

关键词

定态薛定谔方程、含时薛定谔方程、shooting method、matching method、variational Monte Carlo

第一部分：定态薛定谔方程

1. ONE DIMENSION: SHOOTING AND MATCHING METHODS

1.1 Shooting method:

计算原理

1) 对于定态薛定谔方程$-\frac{\bar{h}^2}{2m}\frac{d^2\psi(x)}{dx^2}=(E-V)\psi(x)$,如果将E视为已知参量，则方程为二阶ODE，使用Jacobi方法进行迭代计算可以得到方程数值解
2)当势场$V$有确定宇称时，方程的解也会有确定的宇称，这为我们提供了边界条件：(a)当方程解为奇宇称时，$\psi(0)=0$;(b)当方程解为偶宇称时，$\frac{d\psi(x)}{dx}|_{x=0}=0$
3) 波函数乘以任意常数仍为薛定谔方程的解，因此可以认为偶宇称的波函数$\psi(0)=1$

计算公式

分隔一维空间，间隔为$\Delta x$，$\psi_n=\psi(n\Delta x)$ $V_n=V(n\Delta x)$,令$\bar{h}=m=1$,得到计算式：

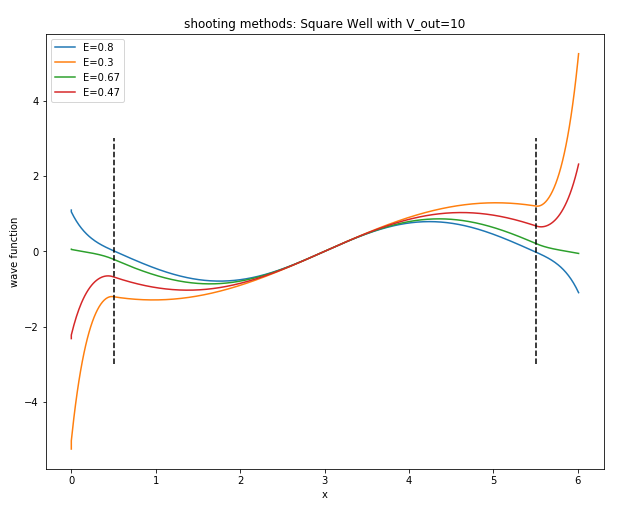
$$\psi_{n+1}=2\psi_n-\psi_{n-1}-2(\Delta x)^2(E-V_n)\psi_n$$ 此外，偶宇称的解满足：$\psi_{-1}=\psi_0=1$；奇宇称的解满足：$\psi_0=0$

计算结果

偶宇称:
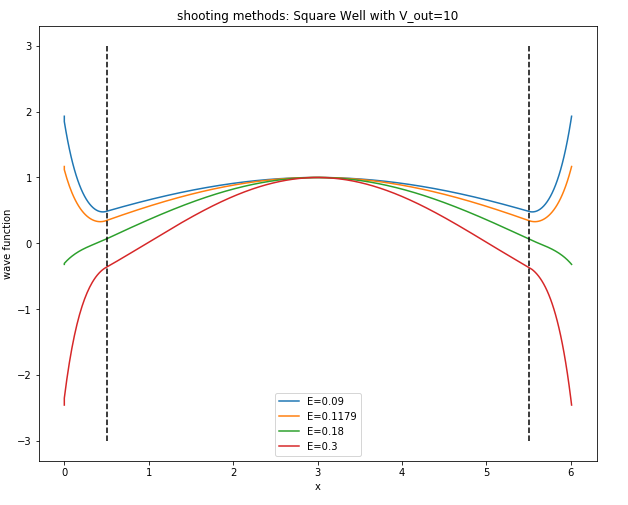
奇宇称:

1.2 matching method:

计算原理

针对Lennard-Jones势场，分头一维直线从左往右迭代和从右往左迭代的结果，然后对参数（能级E）进行调整使两边的迭代结果在交叉点处满足斜率相等，则这个math的结果自然地符薛定谔方程

计算公式

迭代公式与shooting方法相同，迭代的初始条件设置为：$\psi_L(x_L-\Delta x)=-0.0001\Delta x$

计算结果

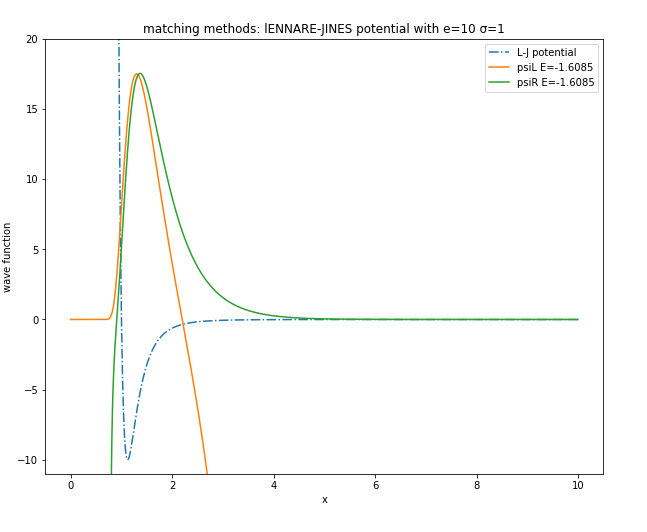
在计算时发现在Lennard-Jones势场对matching method开始迭代的位置要求十分严格，主要是由L-J势场在趋于0位置的发散特性导致的，因此在计算结果中，"matching"的结果并不是很好。
调整能量之前: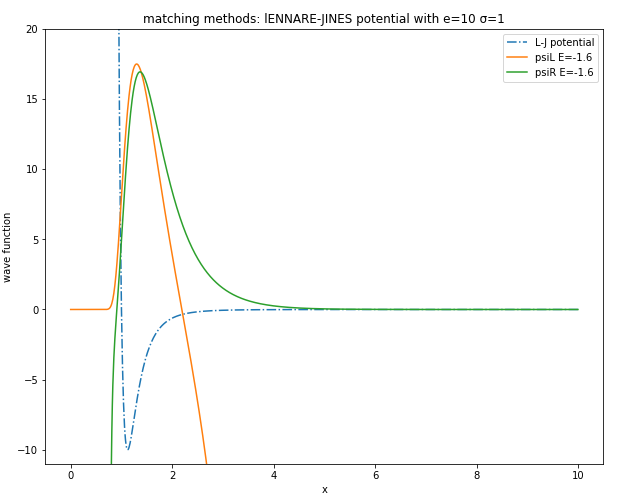
调整能量之后:

2.VARIATIONAL MONTE CARLO (VMC)

说明

一维薛定谔方程数值结果可以用绝大多数可以用以上两种方法求解；或者当势场具有很好的对称性时，也可以将方程化为一维问题求解（例如氢原子问题）。但对于绝大多数的二维三维薛定谔方程，shooting & matching methods 无法设置一维以上的边界条件进而失效。解决此种问题的一般方法是将定态薛定谔方程写成矩阵本征的方程形式进行求解。利用变分Monte Carlo的方法可以计算出多维薛定谔方程。

计算原理

1)确定一个“试探解”$\psi^0(x,y)$，计算其相应的能量$E=\frac{\int\psi^*\hat{H}\psi d\vec{r}}{\int\psi^*\psi d\vec{r}}$;
2)随机选取一个位置$(x_0,y_0)$，令该位置相应的$\psi^{new}(x_0,y_0)=\psi^0(x_0,y_0)\pm d\psi$,此时得到了一个新的$\psi(x,y)$，计算其相应的$E^*$以及$E^*/E$；
3)取一个0到1之间的随机数$r$，比较$r$与$E^*/E$的大小，如果$r>E^*/E$,则保留相应的$\psi(x,y)$和$E^*$作为下一个step的$\psi^0$和$E$，如果$r<E^*/E$,则舍弃掉相应的$\psi(x,y)$和$E^*$

计算公式

1)建立一个矩阵，间隔为$\Delta x=\Delta y=1$,令$\bar{h}=1,m=1/2$，设定初始的试探解

$$\psi^0_{n,m}=\psi^0(n\Delta x,m\Delta y)$$
2) $$E=\frac{\int\psi^*(\Delta+V)\psi d\vec{r}}{\int\psi^*\psi d\vec{r}}=\frac{\sum_{n,m}\psi^*_{n,m}(\frac{\psi_{n+1}+\psi_{n-1}-2\psi_n}{(\Delta x)^2}+\frac{\psi_{m+1}+\psi_{m-1}-2\psi_m}{(\Delta y)^2}+V_{n,m}\psi_{n,m})\Delta x\Delta y}{\sum_{n,m}\psi^*_{n,m}\psi_{n,m}\Delta x\Delta y}$$

计算结果

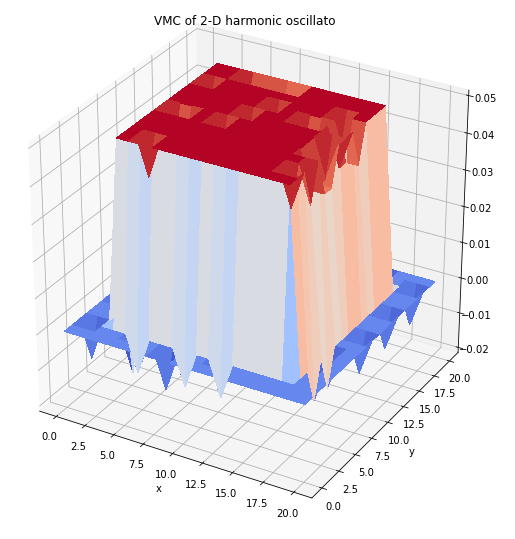
为了计算方便我们首先用VMC方法计算了一维谐振势的波函数，通过计算得到了以下几个结论：
针对一维简谐振子，我最初的想法是能让任意的初始解最终都能解到相应的一维谐振子解，起码是基态，即所有的计算中能量最低的那一个（因为变分原理本身对于量子化的激发态求解就有局域性的问题。）
我们知道一维谐振子的基态波函数为高斯分布的形式，在求解时发现，蒙特卡洛的方法存在着太多问题。
1）计算结果对初始的试探解很敏感，所以是试探解形式的选择尤为重要，这就要求我们对特定的势场其相应的解有大体的了解。一方面初始解不能太多一般，理论上最终总会算出一个最优解，但实际如果用最平庸的初始解（台形），循环上万次甚至十万次都无法计算出；同时又初始解不能太过于接近真实解；在一些资料上看到初始解直接就用的高斯，仅仅是改变$\sigma$,一开始解的算下来结果的确很好，但我觉得这在物理上是不全面的，$\sigma$在物理上的含义代表“经典禁区”，这只不过是在寻找合适的$\sigma$以用来匹配相应的k，并且我的确是没算出一个和参考资料上接近的曲线。

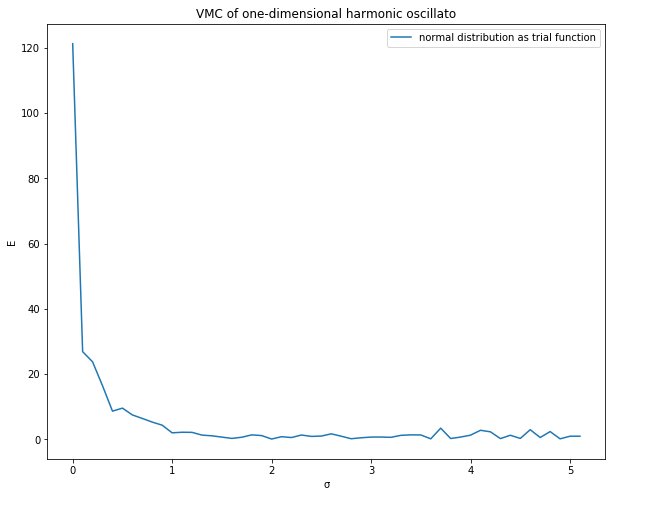
参考资料上的曲线

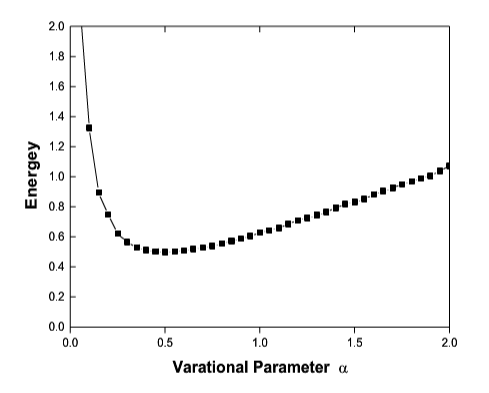
2）虽然蒙特卡洛方法需要大量迭代计算，但在较为简单的蒙卡算法下(判据仅仅是判断所得到的新的能量是否比以前更小)，大量的迭代都是无效的！单纯的增加循环次数并不能得到解，由于随机性，经常是循环了十万次却根本没有新的波函数出现，因为算下来全都是R值比先前更大一些，得到的波函数也没什么意义；
这张图虽然已经计算过但可以看出这一次计算效率为0

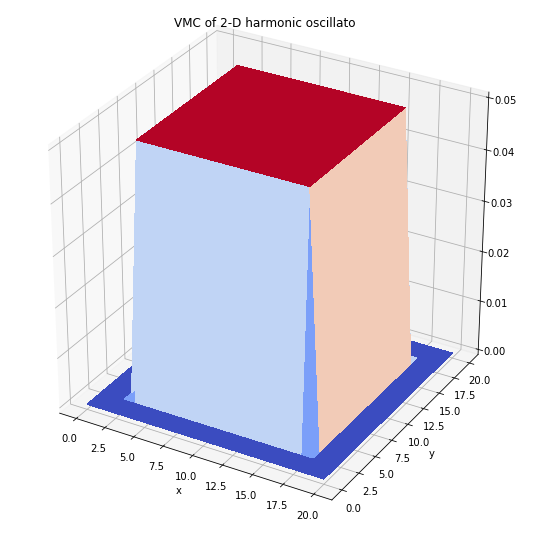
一张失败的蒙卡结果

3）我考虑了一下改进（实际上是两种改进方案，一个是改进判据，另一个是每次随机抽取多个点进行改变而非只选取一个点，但第一种是加一个方差的判据，这种代码比较难从源代码上修改，而且估计加上方差的判据可能计算的效率会更低，所以只做了第二种改进）。实际的效果并不是很好。 （PS：后来和做Ising 模型的同学讨论了一下，本来想在判据那里借用ising 的e指数，也就是波尔兹曼因子作为判据，但后来发现这两者其实一样的。）

第二部分：含时薛定谔方程

1. DIRECT SOLUTIONS

计算原理&计算公式

一维含时薛定谔方程：$i\bar{h}\frac{\partial\psi}{\partial t}=-\frac{\bar{h}^2}{2m}\nabla^2\psi+V(\vec{r})\psi=\hat{H}\psi$ 如果$\hat{H}$与时间无关，可以单独先解时间相关的部分，初步得到解的形式为：

$$\psi(x,y,t)=exp(-it\hat{H}/\bar{h})\psi(x,y,0)$$ 经过$\Delta t$时间段，波函数变为 $$\psi(x,y,t+\Delta t)=exp(-i\Delta t\hat{H}/\bar{h})\psi(x,y,t)$$
e指数近似可以写为 $$exp(-i\Delta t\hat{H}/\bar{h})\approx1-i\Delta t\hat{H}/\bar{h}$$
带回波函数得到 $$\psi(x,y,t+\Delta t)\approx(1-i\Delta t\hat{H}/\bar{h})\psi(x,y,t)$$ $$\psi(m,n,t)=\psi(m\Delta x,n\Delta y,t)$$ 并带入$\hat{H}$的具体形式，得到 $$\psi(m,n,t+\Delta t)=\psi(m,n,t)-i\Delta t(\frac{\psi_{n+1}+\psi_{n-1}-2\psi_n}{(\Delta x)^2}+\frac{\psi_{m+1}+\psi_{m-1}-2\psi_m}{(\Delta y)^2}+V_{n,m}\psi_{n,m})$$ 设$\psi=R+iI$，其中$R$为实部，$I$为虚部，带回上式可以得到实部和虚部的公式为： $$R(m,n,t+\Delta t)=R(m,n,t)+\Delta t(\frac{I_{n+1}+I_{n-1}-2I_n}{(\Delta x)^2}+\frac{I_{m+1}+I_{m-1}-2I_m}{(\Delta y)^2}+V_{n,m}I_{n,m})$$ $$I(m,n,t+\Delta t)=I(m,n,t)-\Delta t(\frac{R_{n+1}+R_{n-1}-2R_n}{(\Delta x)^2}+\frac{R_{m+1}+R_{m-1}-2R_m}{(\Delta y)^2}+V_{n,m}R_{n,m})$$ 将初始条件设置为高斯波包 $$\psi(x,y,t=0)=Cexp[-(x-x_0)^2/\sigma_1^2-(y-y_0)^2/\sigma_2^2]exp(i(k_1x+k_2y))$$

计算结果

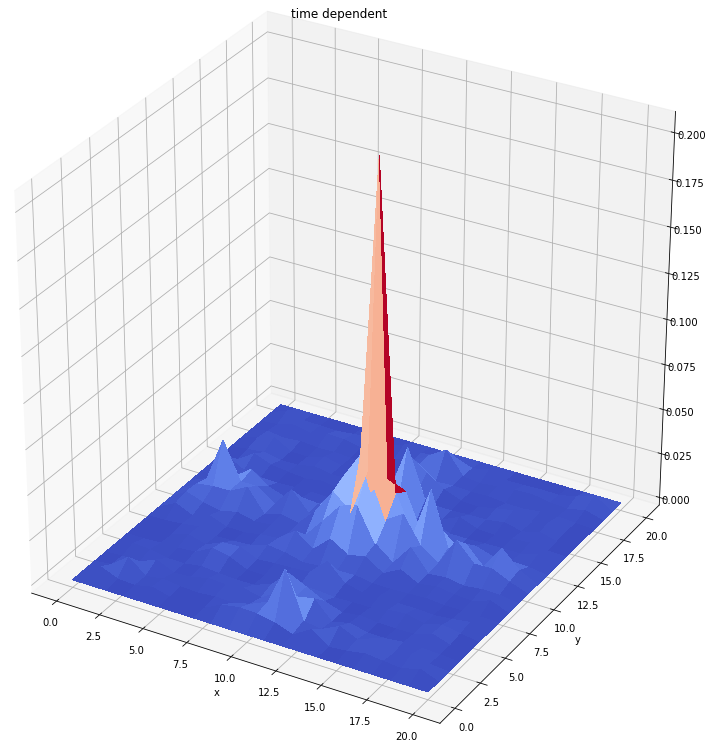
时间循环1个单位

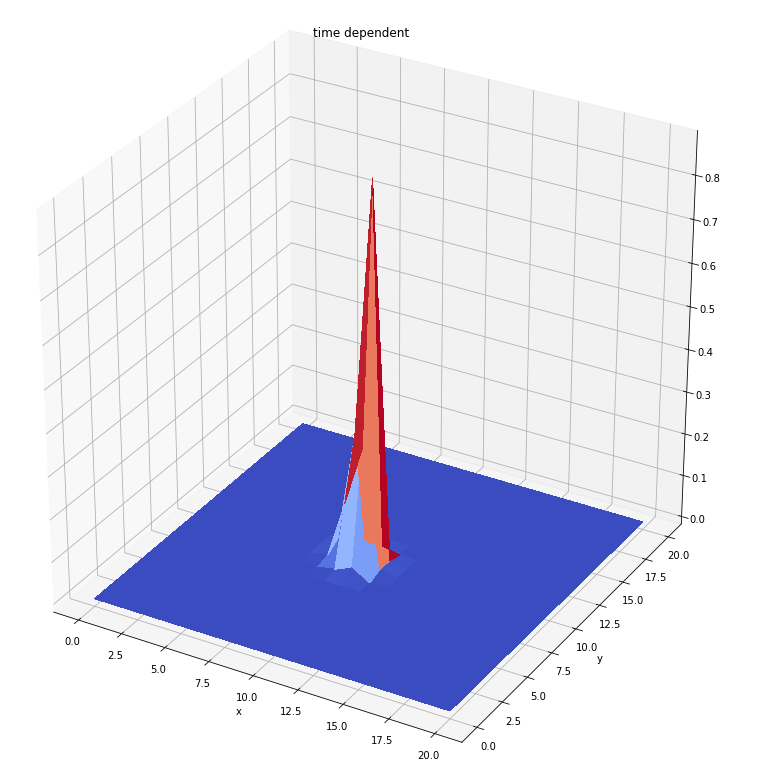
时间循环10个单位

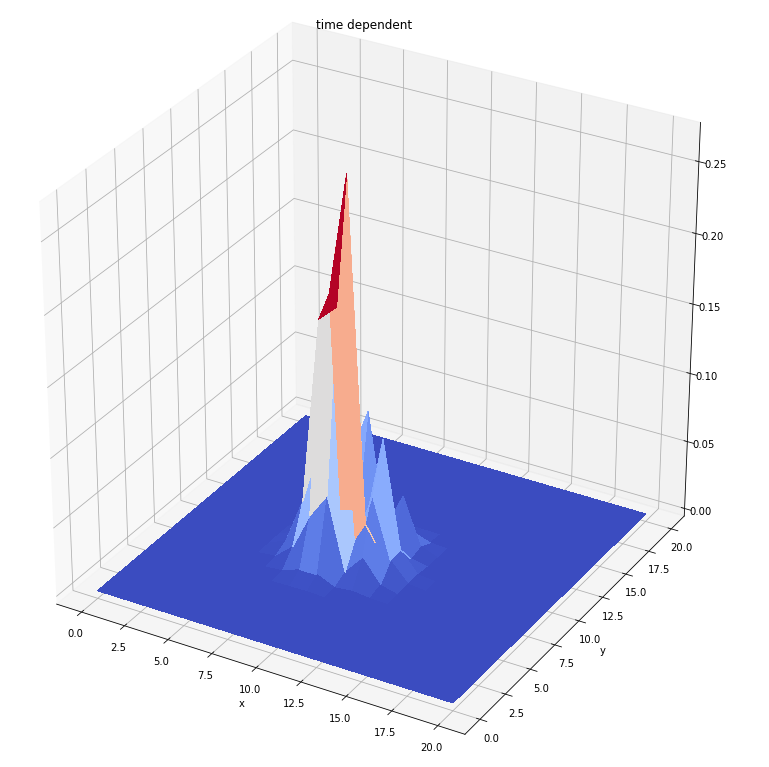
时间循环30个单位

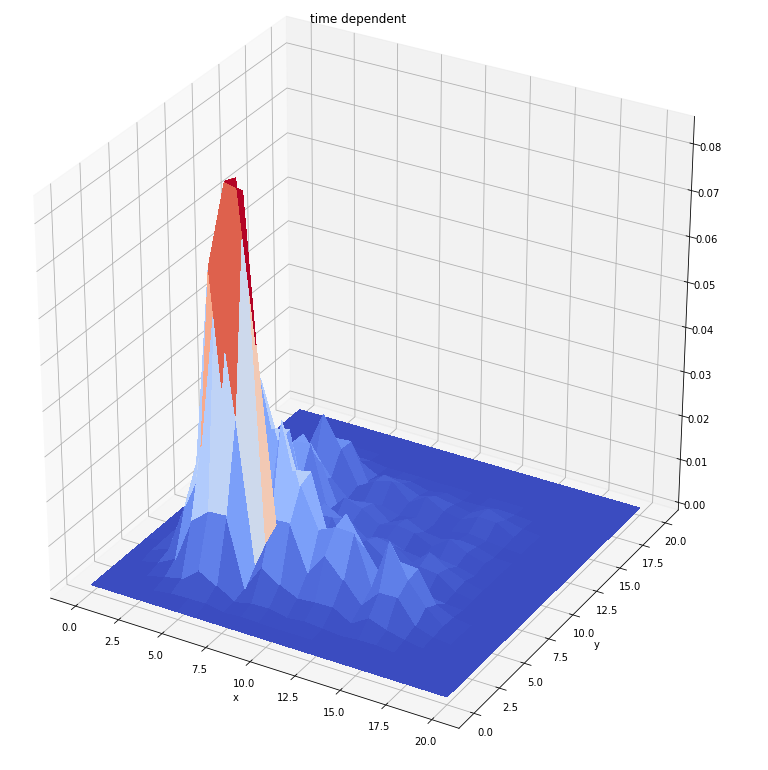
时间循环100个单位

参考资料

• 《计算物理学》（顾昌新 编）
• “变分蒙特卡罗方法求简单谐振子的基态能量”

附录

代码

shooting method
matching method
VMC
time-dependent
以下是我写的VMC的代码的一些改进代码。。。还是想请老师看看问题，虽然还是很low，但我觉得还是比较符合梯度下降法（或者蒙特卡洛吧，蒙卡条件太苛刻了，所以改成了最速下降，但结果还是不怎么样），再给真心有蛮多问题还需要解决。。。

这里重新设置了一下试探解

    psi=np.zeros( (1,31) )
    for j in range (31):
        if j<13:
            psi[0][j]=0
        elif 13<=j<15:
            psi[0][j]=0.5*j-6.5
        elif 15<=j<17:
            psi[0][j]=-0.5*j+8.5
        elif j>17:
            psi[0][j]=0

改变每次随机选取的点的个数为多个

def update(psi):
    psi_u=np.zeros( (1,31) )
    i in range(1,30)
    m=random.sample(i,15)
    n=random.choice([-1.,1.])
    #delta_psi=random.random()*0.01
    delta_psi=0.01
    #k=float(n)
    for j in range (31):
        if j in mm:
            psi_u[0][j]=psi[0][j]-n*delta_psi
        else:
            psi_u[0][j]=psi[0][j]
    return psi_u