Homework 5

---

1.摘要

这个程序使用 Eular 方法解了两个耦合的线性常微分方程，需要用户输入 A,B 的处值 NA，NB， 和 A，B 的时间常数 tauA,tauB, 结束时间 t_end, 以及每次计算的时间间隔 dt。之后画出了 NA，NB 随 t 的数值计算出的变化曲线以及真实曲线。

2.正文

目的是求解以下方程：

$$\frac{dN_A}{dt}=\frac{N_B}{\tau_B}-\frac{N_A}{\tau_A}$$
$$\frac{dN_B}{dt}=\frac{N_A}{\tau_A}-\frac{N_B}{\tau_B}$$

（1）解析解

$N_A,N_B$分别有初值$N_A(0),N_B(0)$,则方程的解析解为：

$$N_A(t)=C_1e^{-\kappa t}+C_2$$
$$N_B(t)=-C_1e^{-\kappa t}+C_2\alpha$$
其中$C_1=\frac{N_A(0)\alpha-N_B(0)}{\alpha+1},C_2=\frac{N_A(0)+N_B(0)}{\alpha+1},\alpha=\frac{\tau _B}{\tau _A}$。

（2）数值解—— Eular 方法

将$N(t+dt)$在$t$处泰勒展开：

$$N(t+dt)=N(t)+\frac{dN(t)}{dt}dt+\frac{1}{2}\frac{d^2N(t)}{dt^2}dt^2+...=N(t)+\frac{dN(t)}{dt}dt$$
得到上式结果忽略了$dt$的高阶项。故对于$N_A(t),N_B(t)$:
$$N_A(t+dt)=N_A(t)+(\frac{N_B}{\tau_B}-\frac{N_A}{\tau_A})dt$$
$$N_B(t+dt)=N_B(t)+(\frac{N_A}{\tau_A}-\frac{N_B}{\tau_B})dt$$

(3)程序

这是完整代码
首先引用库：

import pylab as plb
import math

之后建立各个物理量的$list$：

NA=[]        #establish a list corresponding to NA
NB=[]        #establish a list corresponding to NB
True_NA=[]   #establish a list corresponding to True NA
True_NB=[]   #establish a list corresponding to True NB
t=[]         #establish a list corresponding to t

然后提示用户输入数据，之后计算每个时刻的数值计算出的$N_A(t),N_B(t)$,和真实的$N_A(t),N_B(t)$，并把他们添加到各自的$list$中去：

for i in range(int(t_end/dt)):
    NA.append(NA[i]+(NB[i]/tauB-NA[i]/tauA)*dt)
    NB.append(NB[i]+(NA[i]/tauA-NB[i]/tauB)*dt)
    True_NA.append(C1*math.exp(-(i+1)*dt*(alpha+1)/tauB)+C2)
    True_NB.append(-C1*math.exp(-(i+1)*dt*(alpha+1)/tauB)+C2*alpha)
    t.append((i+1)*dt)

最后打印结果并画图。

3.结果

用户输入的数据：

数值计算的结果：

其中，第一个 $list$ 是 $t$,第二个 $list$ 是 $N_A(t)$,第三个 $list$ 是 $N_B(t)$。

数值计算以及真实值曲线：

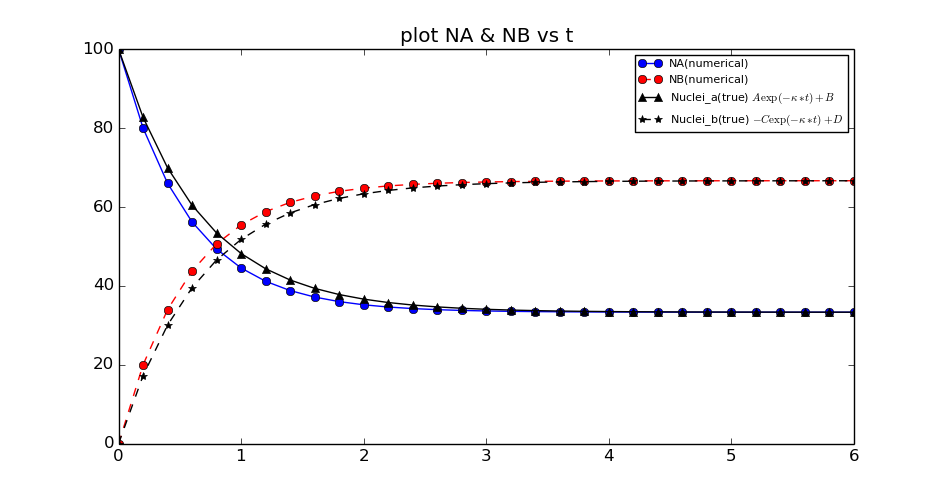
并且当 $t \to \infty$ 时，有 $\frac{N_A(\infty)}{N_B(\infty}=\frac{\tau_A}{\tau_B}$。

4.致谢

之前我的作业中并没有解析解的部分，但是在参考了2013301020145陈锋同学的作业后，我加上了这部分。