HOMEWORK9——Pendulum

homework
ahthor : 2013301020086 Yuqi Wang

---

1.Abstract

This homework is studying the behaviours of a physical pendulum, which is a standard chaos system. I learned that in some cases the system will be chaotic when the behaviours of the pendulum is unpredictable but deterministic, and if I choose some special point in the phase space, the attractor appears.

2. Introduction

The ordinary differencial equition of a physical pendulem with driven and dissipation force is:

$$\frac{d^2\theta}{dt^2}=-\frac{g}{l}sin\theta-q\frac{d\theta}{dt}+F_Dsin(\Omega_Dt)$$
where the $g=9.8m/s^2$ is the gravity acceleration, $l=9.8m$ is the length of the pendulum, $q=0.5s^{-1}$ is the dissipation parameter, $F_D$ and $\Omega_D=\frac{2}{3}$ are the amplitude and angular frequency of the driven force, respectively.

The word chaotic means that even though you change the initial condition tinily, the difference of the terminal point might be as that between Jesus and Satan. But this does not mean it is unpredictable, on the contrary, since we have the ODE and the initial condition, we can find every step the pendulum will go on numerically, in other words, we can find the trajectory of the pendulum in the phase space merely with a negligible error, as long as we can choose the time interval between every step enough small.

3.Method and procedure

This is the complete code
Eular-Cromer method is performed as following:

$$\omega_{i+1}=\omega_i+[-\frac{g}{l}sin\theta_i-q\omega_i+F_Dsin(\Omega_Dt_i)]\Delta t$$
$$\theta_{i+1}=\theta_i+\omega_{i+1}\Delta t$$
If $\theta_{i+1}$ is out of the range $[-\pi,\pi]$, add or subtract $2\pi$ to keep it in this range.

When I chose the parameter $F_D=0.5, \Omega_D=\frac{2}{3}$, there is no chaotic behaviour in phase space.

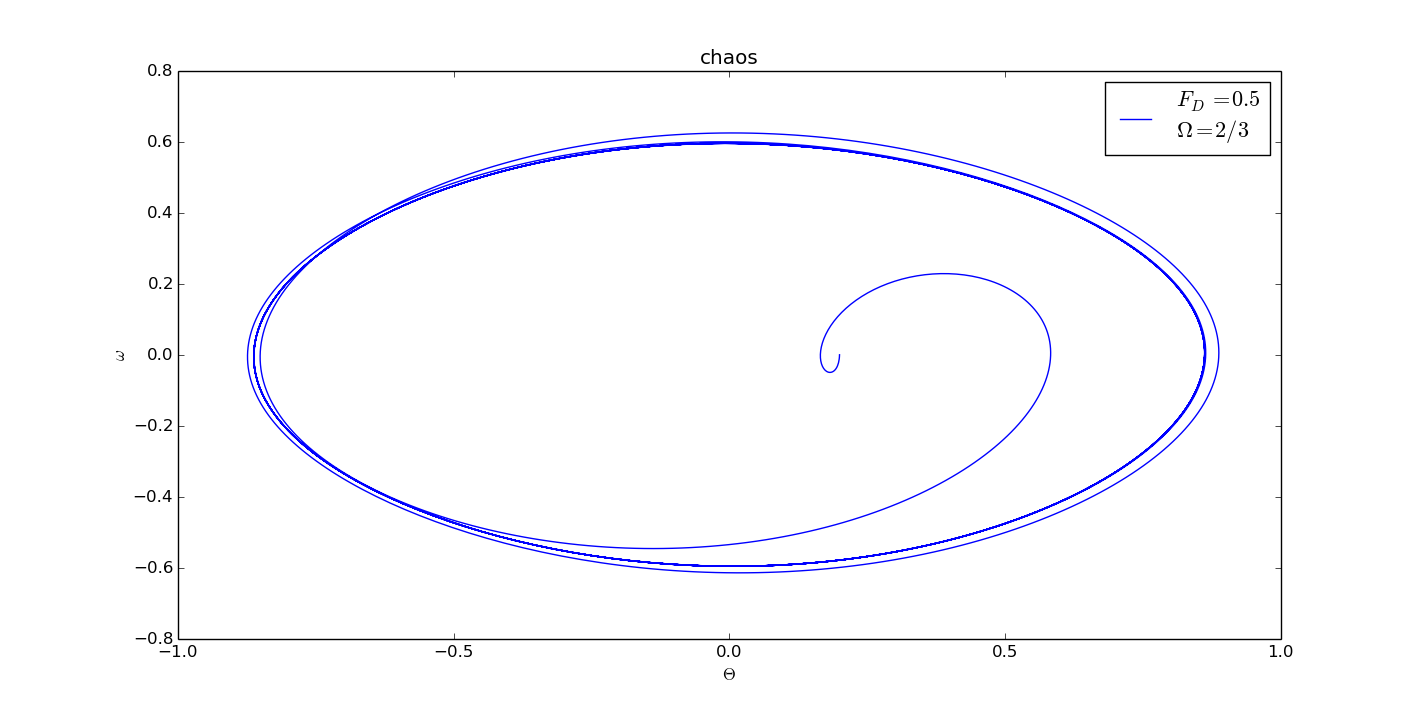
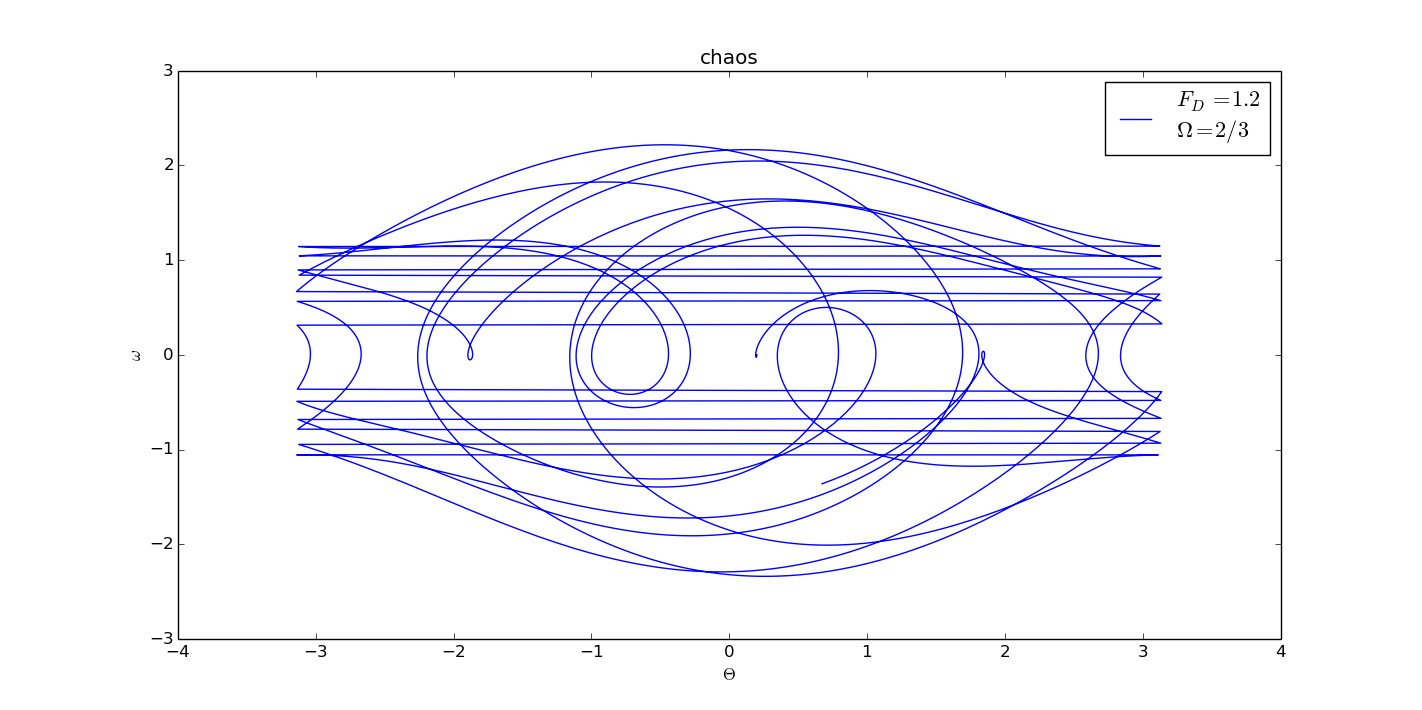
While I adjusted the $F_D=1.2$, chaos appeared.

When I selected some special point such that $\Omega_Dt_i\approx2\pi n$, where $n$ is any arbitrary integer, I saw the attractor.

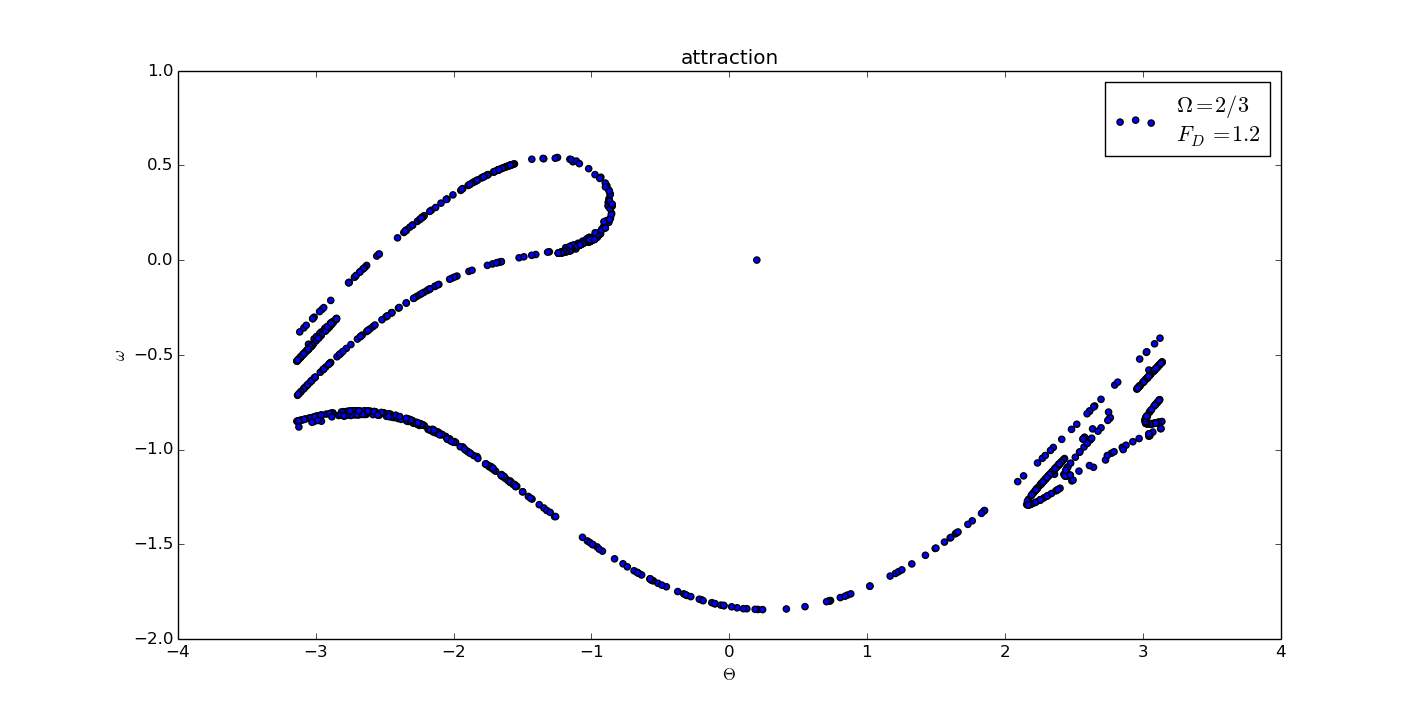
I chose the time interval $dt=\frac{2\pi}{200\Omega_D}$, so I merely selected the point whose index $i$ satisfied $i$ mod $200 = 0$.

But when I disturbed the $F_D$ slightly, the attractor disappeared.

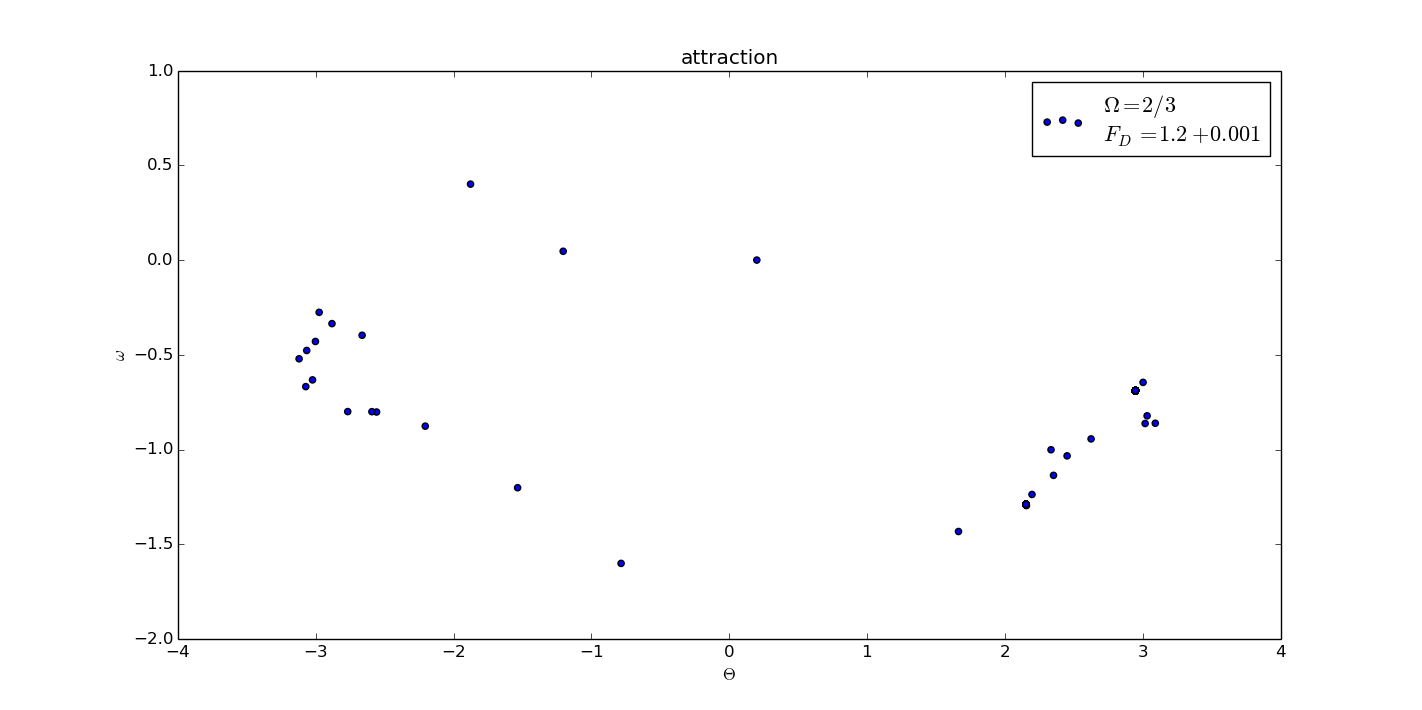
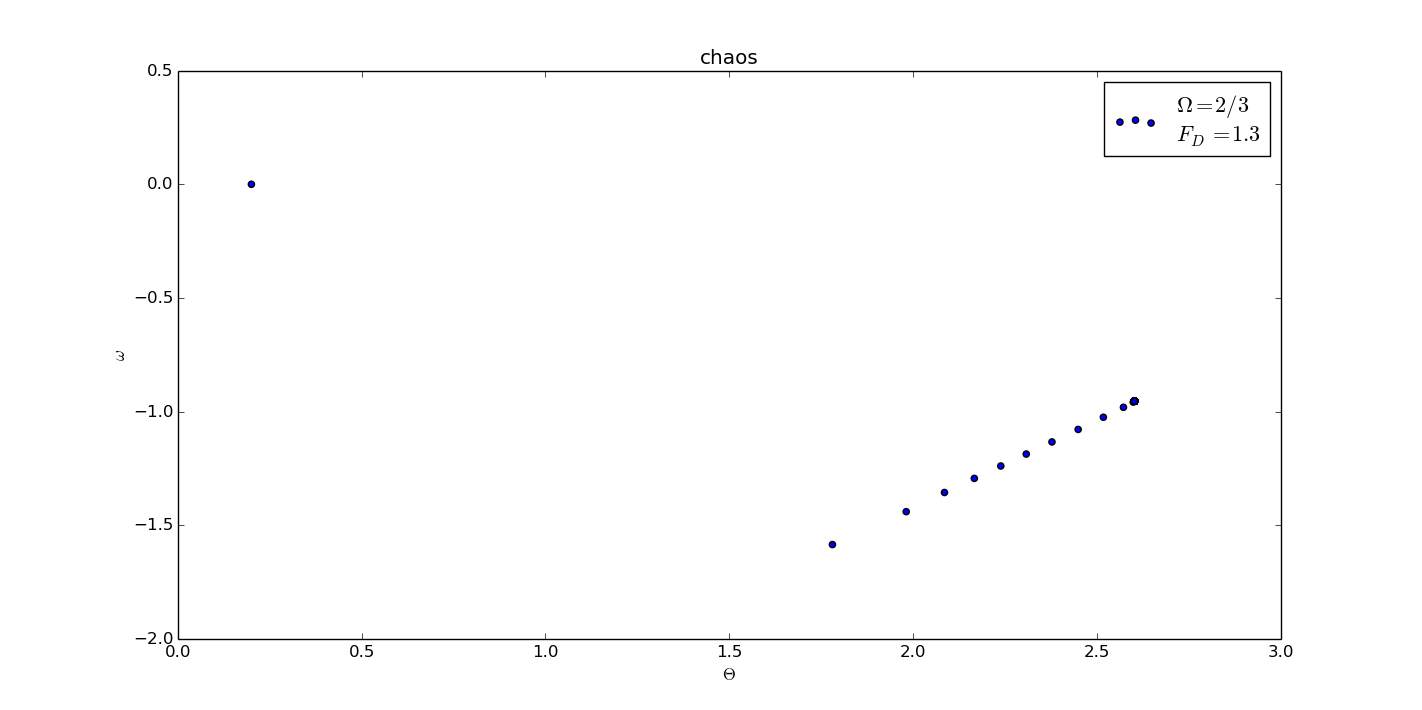
4.Conclution

The chaotic system is seemed to be disordered but if we select a point every period of the driven force, we can see the attractor, while this feature is appeared only in some spacial cases. If I change the amplitude of the driven force, the attractor disappears.