6.2 参数估计

高等工程数学 讲义 2025AU

---

---

参数估计的数学描述

• 设总体 $X$ 的分布函数为 $F(x;\theta)$，其中 $\theta$ 是 未知参数.
• $\theta$ 的取值范围已知，即已知 $\theta\in\Theta$.
  
  • $\Theta$ 称为 参数空间.
• 从总体中抽取样本 $X_1,X_2,\ldots,X_n$.
• 根据该样本对未知参数 $\theta$ 做出估计.

---

参数的点估计(Point Estimation)

1. 矩估计
2. 最大似然估计
3. Bayes估计
4. 最小二乘估计

---

6.2.1 矩估计（Method of Moments）

• 基本思想：
  
  • 用样本矩近似总体矩，进而求解其中的参数（估计）值.
  • 最初由俄国数学家 Pafnuty Chebyshev 在 1887 年提出.
• 理论基础：Khinchin大数定律
  
  • 设 $\{X_i\}$ 是独立同分布的随机变量列，若 $X_i$ 的数学期望 $\mu$ 存在，则 $\{X_i\}$ 服从大数定律.
  • 即：对任意的 $\varepsilon>0$, $\displaystyle\lim_{n\to\infty}P\left\{\left|\frac1n\sum_{i=1}^nX_i-\mu\right|>\varepsilon\right\}=0$.
  • 随着样本容量的增加，样本矩将越来越接近于总体矩.

---

Pafnuty Chebyshev

• Пафну́тий Льво́вич Чебышёв (1821-1894)
• considered to be a founding father of Russian mathematics. Among his well-known students were the mathematicians Dmitry Grave, Aleksandr Korkin, Aleksandr Lyapunov, and Andrei Markov.
• Chebyshev Inequality: $\displaystyle \operatorname{Pr}(|X-\mathbf{E}(X)| \geq a \sigma) \leq \frac{1}{a^{2}}$

---

矩

设 $X_1, X_2, ..., X_n$ 是来自总体 $X$ 的样本

• 总体 $k$ 阶矩：$\displaystyle \bbox[lightgreen]{\mu_{k}=E\left(X^{k}\right)}$.
• 样本 $k$ 阶矩：$\displaystyle \bbox[yellow]{A_{k}=\frac{1}{n} \sum_{i=1}^{n} X_{i}^{k}}$.
• 理论上，总体 $k$ 阶矩和样本 $k$ 阶矩并不相等.
  
  • 前者是未知的常数，是确定的.
  • 后者是变量，是存在波动的.
• 但由 Khinchin 大数定律，$\bbox[yellow]{A_{k}} \stackrel{P}{\longrightarrow} \bbox[lightgreen]{\mu_{k}}, (n \rightarrow \infty)$.

---

矩估计的求解

设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim F(x;\theta)$ 的简单随机样本，其中 $\theta=(\theta_1,\theta_2,...,\theta_k)\in\Theta$ 是待估的未知参数.

1. 求总体 $X$ 的前 $k$ 阶矩 $\mu_{i}\left(\theta_{1}, \theta_{2}, \cdots, \theta_{k}\right)=E\left(X^{i}\right),\; (i=1, 2, \dots, k).$
2. 求样本的前 $k$ 阶矩 $\displaystyle A_{i}=\frac{1}{n} \sum_{l=1}^{n} X_{l}^{i},\; (i=1, 2, \dots, k)$.
3. 解方程（组）：$\mu_{i}\left(\theta_{1}, \theta_{2}, \cdots, \theta_{k}\right)=A_{i}, \quad (i=1,2, \cdots, k)$,
   
   • 得 $\hat{\theta}_{i}=\hat{\theta}_{i}\left(X_{1}, X_{2}, \cdots, X_{n}\right), \quad (i=1,2, \cdots, k)$.
   • 称 $\hat{\theta}_{i}\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 为 $\theta_i$ 的 矩估计量 (Moment Estimator).
   • 称 $\hat{\theta}_{i}\left(x_{1}, x_{2}, \cdots, x_{n}\right)$ 为 $\theta_i$ 的 矩估计值 (Moment Estimate).

---

Poisson 强度的矩估计

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim P(\lambda)$ 的样本，求参数 $\lambda$ 的矩估计.

• 解： Poisson分布的分布律 $\displaystyle P\{X=k\}=\frac{\lambda^{k}}{k !} e^{-\lambda} \quad(\lambda>0, k=0,1,2, \cdots)$.
• 总体一阶矩和样本一阶矩分别为 $E(X)=\lambda$，$\displaystyle \overline{X}=\frac{1}{n} \sum_{i=1}^{n} X_{i}$.
• 令 $\overline{X}=\overline{X}$，求得参数 $\lambda$ 的矩估计(量)为 $\hat{\lambda}=\overline{X}$.

---

总体方差的矩估计

引理 设 $X_1, X_2, ..., X_n$ 是来自总体 $X$ 的样本，设总体 $X$ 的二阶矩存在，则

1. 样本均值是总体均值 $\mu=E(X)$ 的矩估计.
2. 样本方差 $\displaystyle S^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}$ 是总体方差 $\sigma^2=D(X)$ 的矩估计.

---

例 袋中有红球和黑球共 $10$ 只. 现从袋中有放回地次取个球出来观测其颜色，直到取到红球为止，此时记取球的总次数为 $X$. 若这样的试验一共进行了 $6$ 次，得到的数据分别是

$$4,\;6,\;4,\;5,\;7,\;6$$

试求袋中红球数的矩估计.

---

解： 设袋中共有 $10p$ 个红球. $X$ 表示第一次摸到红球时摸球的总次数. 则

$$P\{X=k\}=(1-p)^{k-1}p.$$

进而 $\displaystyle E(X)=\sum_{k=1}^{\infty}kP\{X=k\}=\sum_{k=1}^{\infty}k(1-p)^{k-1}p=\frac1p$.

样本矩 $\displaystyle A_1=4\times\frac13+5\times\frac16+6\times\frac13+7\times\frac16=\frac{16}3$.

令 $E(X)=A_1$，即 $\displaystyle \frac1p=\frac{16}3$，解得 $p=\frac{3}{16}=0.1875$.

综上，袋中的红球数约为 $10p\approx 2$.

---

对矩估计法的评价

1. 原理直观，是一种古老的参数估计方法.
2. 只用到总体矩，方法简单.
   
   • 如果总体矩不存在，则无法求参数的点估计.
   • 例如，设总体服从Cauchy分布，其密度函数为 $\displaystyle f(x ; \theta)=\frac{1}{\pi} \cdot \frac{1}{1+(x-\theta)^{2}}$，因为总体的数学期望不存在，故 $\theta$ 的矩估计不存在！
3. 没有用到总体的分布形式，总体包含的信息没有得到充分利用.
4. 基于大数定律，在大样本下矩估计才有较好的效果.

---

均匀分布参数的矩估计

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim U(a,b)$ 的简单随机样本，其中 $a<b$ 是未知参数，求 $a,b$ 的矩估计.

• 提示： $\displaystyle E(X)=\frac{a+b}2$，$\displaystyle D(X)=\frac{(b-a)^2}{12}$.
• 令 $\displaystyle \left\{\begin{array}{l}{\overline{X}=\frac{a+b}{2}} \\ {S^{2}=\frac{(b-a)^{2}}{12}}\end{array}\right.$, 解得 $\left\{\begin{array}{l}{\hat{a}=\overline{X}-\sqrt{3} S} \\ {\hat{b}=\overline{X}+\sqrt{3} S}\end{array}\right.$

---

讨论： 假设有如下来自 $X\sim U(a,b)$ 的观测值

$$\begin{array}{} 0.4387,&0.3816,&0.7655,&0.7952,&0.1869,&0.4898,&0.456,&0.6463,\\ 0.7094,&0.7547,&0.2760,&0.6797,&0.6551,&0.1626,&\bbox[lightgreen]{0.1190},&0.4984,\\ \bbox[yellow]{0.9597},&0.3404,&0.5853,&0.2238,&0.7513,&0.2551,&0.5060,&0.6991,\\ 0.8909,&0.9593,&0.5472,&0.1386,&0.1493,&0.2575,&0.8407,&0.2543,\\ 0.8143,&0.2435,&0.9293,&0.3500,&0.1966,&0.2511,&0.6160,&0.4733 \end{array}$$

• 计算得到 $\overline{x}=0.606928$，$s=0.254063$.
• 进而得到 $\hat{a}=0.0602,\quad \hat{b}=0.9516$.
• 数据中的最大和最小值分别是 $\bbox[yellow]{0.9597}$ 和 $\bbox[lightgreen]{0.1190}$，对均匀分布而言，似乎这才是更合理的参数估计值.
• 问题： 是否有比矩估计更加“合理”的估计？

---

6.2.2 最大似然估计

---

最大似然

• 基本思想
  
  • 随机事件 $\{X\in D\}$ 的概率 $P\{X\in D\}$ 由 $X$ 的分布 $F(x;\theta)$ 确定, 而分布又由参数 $\theta$ 决定.
  • 在已经掌握了样本，也即具体发生的事件的情况下，有理由相信这个已经发生的事件就是最有可能发生的事件.
  • 基于“最大可能”的思想来确定参数的估值，就是要找一个估计值 $\hat{\theta}$，使得已发生事件的概率最大.
• The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference.[1]

---

最大似然估计（Maximum Likelihood Estimation）

• Early users of maximum likelihood were C.F. Gauss, P.S. Laplace, etc.
• However, its widespread use rose between 1912 and 1922 when Ronald Fisher recommended, widely popularized, and carefully analyzed maximum-likelihood estimation.

---

R. A. Fisher

• Sir Ronald Aylmer Fisher (1890-1962)
  
  • 英国统计学家、演化生物学家与遗传学家，现代统计学与现代进化论的奠基者之一.
• "a genius who almost single-handedly created the foundations for modern statistical science".
• "the single most important figure in 20th century statistics".
• "the greatest of Darwin’s successors".

---

例 一老战士与一新战士的射击命中率分别为 $0.9$ 和 $0.5$，在射击训练中每人各打三枪. 训练结束后现场留有一张靶纸. 如果靶纸上有 $3$ 个弹孔，试问这张靶纸最有可能是谁的？如果靶纸上只有 $1$ 个弹孔，试问这张靶纸又最有可能是谁的？

---

分析： 设靶纸上出现的弹孔数为 $X$，则 $X$ 服从二项分布

$\displaystyle P\{X=k\}=\binom{3}{k} p^{k}(1-p)^{3-k} \;(k=0,1,2,3)$

---

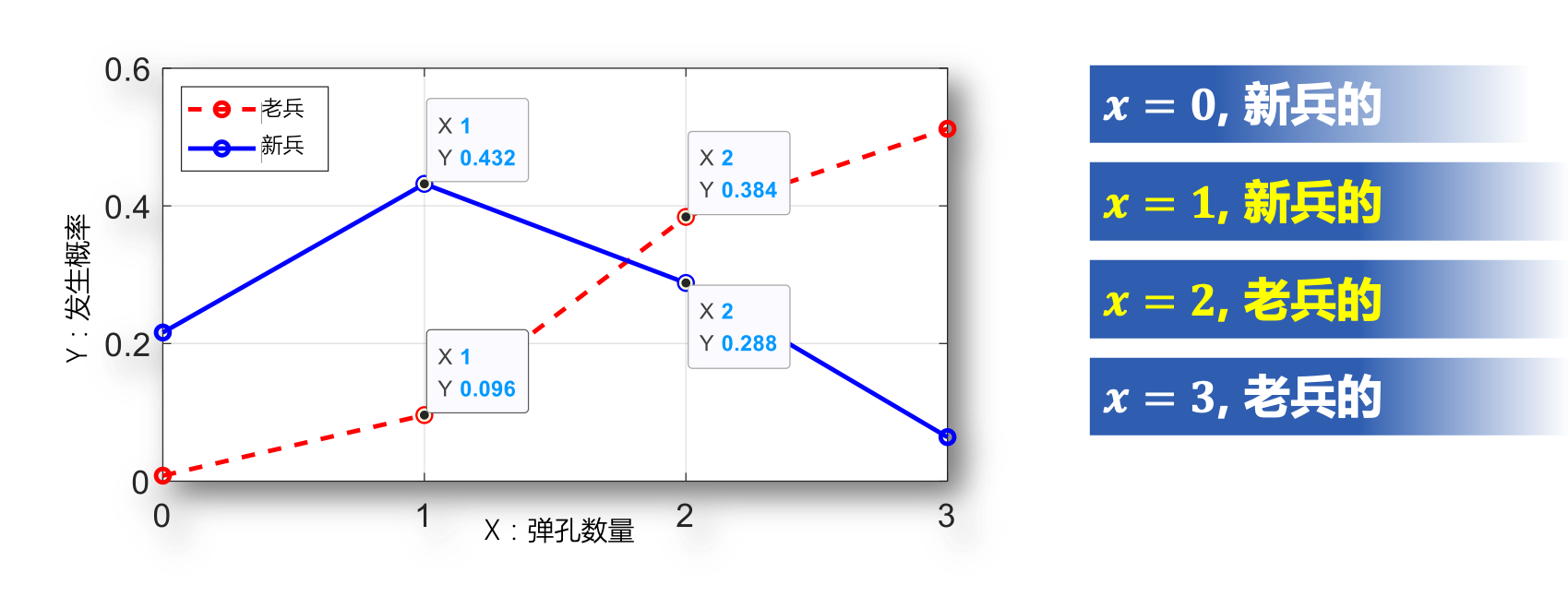
最大似然估计

设 $X_1, X_2, ..., X_n$ 是来自总体 $X$ 的样本，$x_1,x_2,\ldots,x_n$ 为其观测值，记

$$\displaystyle L(\theta)=\left\{\begin{array}{ll} {\prod_{i=1}^{n} P\left\{X_{i}=x_{i}\right\}} & \text{若}X\text{是离散型随机变量}\\ {\prod_{i=1}^{n} f\left(x_{i} ; \theta\right)} & \text{若}X\text{是连续型随机变量} \end{array}\right.$$

称 $L(\theta)$ 是 似然函数 (Likelihood).

1. 若统计量 $\hat{\theta}\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 满足 $L(\hat{\theta})=\max _{\theta} L\left(\theta\right)$，则称其为 $\theta$的 最大似然估计(量) (Maximun Likelihood Estimator，简写：MLE).
   
   • 最大似然的思想用一句话可以概括为：参数看上去最像什么值，就用这个值作为参数的估计.

---

均匀分布参数的极大似然估计

例 设 $X_1,X_2,…,X_n$ 是总体 $X\sim U(a,b)\;(a<b)$ 的简单随机样本，试求参数 $a$ 和 $b$ 的 MLE.

提示：

• 似然函数$\displaystyle L(a, b)=\prod_{i=1}^{n} \frac{1}{b-a}=(b-a)^{-n}, \quad \left(a\leq x_{(1)}, x_{(n)}\leq b\right)$,
  
  • 其中 $\displaystyle x_{(1)}=\min _{1 \leq i \leq n}\left\{x_{i}\right\}, x_{(n)}=\max _{1 \leq i \leq n}\left\{x_{i}\right\}$.
• 令 $\displaystyle \left\{\begin{array}{l}{\frac{\partial L}{\partial a}=n(b-a)^{-(n+1)}=0} \\ {\frac{\partial L}{\partial b}=-n(b-a)^{-(n+1)}=0}\end{array} \quad\left(a\leq x_{(1)}, x_{(n)}\leq b\right)\right.$，从该方程显然无法直接求得 MLE.
• 考虑到参数的取值范围，$a,b$ 的 MLE 应该是 $\hat{a}=X_{(1)}, \; \hat{b}=X_{(n)}$.

---

指数分布参数的最大似然估计

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim\mathrm{Exp}(\theta)$ 的简单随机样本，其中 $\theta>0$ 是未知参数，试求 $\theta$ 的 MLE.

提示：

• $X\sim\mathrm{Exp}(\theta)$ 的密度函数 $\displaystyle f(x ; \theta)=\left\{\begin{array}{l} \frac{1}{\theta} \mathrm{e}^{-\frac{x}{\theta}}, & {x>0} \\ {0}, & {x \leq 0}\end{array}\right.\quad(\theta>0)$.
• 似然函数 $\displaystyle L(\theta)=\prod_{i=1}^{n} \frac{1}{\theta} \mathrm{e}^{-\frac{x_{i}}{\theta}}=\theta^{-n} \mathrm{e}^{-\frac{1}{\theta} \sum\limits_{i=1}^{n} x_{i}}=\theta^{-n} \mathrm{e}^{-\frac{n \overline{x}}{\theta}}$.
• 考虑到 $L(\theta)$ 和 $\ln L(\theta)$ 的极值点相同，故令$\displaystyle \frac{\operatorname{dln} L(\theta)}{\mathrm{d} \theta}=-\frac{n}{\theta}+\frac{n \overline{x}}{\theta^{2}}=0$.
• 求解该方程（对数似然方程），可得 $\hat{\theta}=\overline{X}$.

---

正态总体参数的最大似然估计

例 设 $X_1,X_2,…,X_n$ 是来自总体 $X\sim N(\mu,\sigma^2 )$ 的简单随机样本，求 $\mu$ 和 $\sigma^2$ 的 MLE.

提示：

• $\displaystyle L\left(\mu, \sigma^{2}\right)=\prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi} \sigma} \mathrm{e}^{-\frac{\left(x_{i}-\mu\right)^{2}}{2 \sigma^{2}}}=(\sqrt{2 \pi}\sigma)^{-n} \mathrm{e}^{-\frac{1}{2 \sigma^{2}} \sum\limits_{i=1}^{n}\left(x_{i}-\mu\right)^{2}}$.
• 令 $\left\{\begin{aligned} \frac{\partial \ln L}{\partial \mu} &=\frac{1}{\sigma^{2}} \sum_{i=1}^{n}\left(x_{i}-\mu\right)=0 \\ \frac{\partial \ln L}{\partial\left(\sigma^{2}\right)} &=-\frac{n}{2 \sigma^{2}}+\frac{1}{2 \sigma^{4}} \sum_{i=1}^{n}\left(x_{i}-\mu\right)^{2}=0 \end{aligned}\right.$
• 解得 $\hat{\mu}=\overline{X}$，$\displaystyle \hat{\sigma}^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}={S}^{2}$.

---

求 MLE 的一般步骤

1. 根据总体的分布，写出似然函数 $L\left(\theta_{1}, \theta_{2}, \ldots, \theta_{m}\right)$;
2. 写出 对数似然函数 $\ln L\left(\theta_{1}, \theta_{2}, \ldots, \theta_{m}\right)$;
3. 写出 对数似然方程(组)
   
   • $\displaystyle \frac{\partial}{\partial \theta_{i}}\ln L\left(\theta_{1}, \theta_{2}, \ldots, \theta_{m}\right)=0, \quad (i=1,2,\ldots, m)$.
4. 解出 $\hat{\theta}_i$ 即为 $\theta_i$ 的MLE.
   
   • 如果由对数似然方程(组)无法确定 MLE，则结合参数取值的边界条件，对似然函数进行讨论.

---

例 设 $X_1,X_2,\ldots,X_n$ 是来自总体 $X\sim b(m,p)$ 的简单随机样本，其中 $p\in(0,1)$ 为未知参数，求 $p$ 的矩估计 $\hat{p}_M$ 和最大似然估计 $\hat{p}_L$.

提示：

• $E(X)=mp$.
• 由矩估计法，令 $\overline{X}=E(X)$，即 $\overline{X}=mp$.
• 解得 $\displaystyle p=\frac{\overline{X}}m$.
• 故 $p$ 的矩估计为 $\displaystyle \hat{p}_M=\frac{\overline{X}}m$.

---

• $X$ 的分布律为
  
  • $P\{X=k\}=\left(\begin{array}{c}{m} \\ {k}\end{array}\right) \cdot p^{k} \cdot(1-p)^{m-k}$，$k=0,1,2, \cdots, m$.
• 似然函数
  
  • $\displaystyle L(p)=\prod_{i=1}^{n}\left(\begin{array}{c}{m} \\ {x_{i}}\end{array}\right) \cdot p^{x_{i}} \cdot(1-p)^{m-x_{i}}=\left[\prod\limits_{i=1}^{n}\left(\begin{array}{c}{m} \\ {x_{i}}\end{array}\right)\right] \cdot p^{\sum\limits_{i=1}^{n} x_{i}} \cdot(1-p)^{m{n}-\sum\limits_{i=1}^{n} x_{i}}$.
• 对数似然函数 $\displaystyle \ln L(p)=\ln \left[\prod_{i=1}^{n}\left(\begin{array}{c}{m} \\ {x_{i}}\end{array}\right)\right]+\sum_{i=1}^{n} x_{i} \cdot \ln p+\left(mn-\sum_{i=1}^{n} x_{i}\right) \cdot \ln (1-p).$

---

• 令 $\displaystyle \frac{\mathrm{d} \ln L(p)}{\mathrm{d} p}=0$, 即：$\displaystyle \frac{\sum\limits_{i=1}^{n} x_{i}}{p}-\frac{mn-\sum\limits_{i=1}^{n} x_{i}}{1-p}=0$.
• 由此解得 $\displaystyle p=\frac{1}{m} \left(\frac{1}{n} \sum_{i=1}^{n} x_{i}\right)$.
• 从而 $p$ 的最大似然估计 $\displaystyle \hat{p}_L=\frac{\overline{X}}{m}$.
• 二项分布的参数 $p$ 的矩估计和 MLE 相同.

---

例 设总体 $X$ 的密度函数为

$$f(x ; \theta)=\left\{\begin{array}{cc}{\theta,} & {0<x<1} \\ {1-\theta,} & {1 \leq x<2} \\ {0,} & {\text {其他}}\end{array}\right.$$

其中 $0\leq\theta\leq1$ 为未知参数. 设 $X_1, X_2, ..., X_n$ 是来自总体 $X$ 的简单随机样本，求 $\theta$ 的矩估计 $\hat{\theta}_M$ 和最大似然估计 $\hat{\theta}_L$.

---

提示

• $\displaystyle E(X)=\int_{-\infty}^{+\infty} x \cdot f(x ; \theta) \mathrm{d} x=\int_{0}^{1} x \cdot \theta \mathrm{d} x+\int_{1}^{2} x \cdot(1-\theta) \mathrm{d} x=\frac32-\theta$.
• 令 $\displaystyle \frac32-\theta=\overline{X}$, 解得 $\theta$ 的矩估计 $\displaystyle \hat{\theta}_M=\frac32-\overline{X}$.
• 设 $k\;(k=0,1,\ldots,n)$ 为抽样结果落在 $(0,1)$ 中的次数.
• 似然函数 $\displaystyle L(\theta)=\prod_{i=1}^{n} f\left(x_{i} ; \theta\right)=\theta^{k} \cdot(1-\theta)^{n-k}$.
• 对数似然函数 $\ln L(\theta)=k \cdot \ln \theta+(n-k) \cdot \ln (1-\theta)$.
• 令 $\displaystyle \frac{\mathrm{d} \ln L(\theta)}{\mathrm{d} \theta}=0$, 即：$\displaystyle \frac{k}{\theta}-\frac{n-k}{1-\theta}=0$.
• 由此解得 $\theta$ 的最大似然估计 $\displaystyle \hat{\theta}_L=\frac{k}{n}$.

---

例 设总体 $X$ 的分布律为

$$\begin{array}{l} P\{X=-1\}=\theta^2,\\ P\{X=0\}=2\theta(1-\theta),\\ P\{X=1\}=(1-\theta)^2. \end{array}$$

设 $X_1, X_2, ..., X_n$ 是来自总体 $X$ 的样本，试求 $\theta$ 的矩估计和最大似然估计.

---

提示：

• $E(X)=(-1)\theta^2+(1-\theta)^2=1-2\theta$.
• 令 $E(X)=\overline{X}$, 解得 $\theta$ 的矩估计 $\displaystyle \hat{\theta}_M=\frac12\left(1-\overline{X}\right)$.
• 设 $X$ 取 $-1,0,1$ 的次数分别为 $k_1,k_2,k_3$, $(k_1+k_2+k_3=n)$.
• 似然函数 $\displaystyle L(\theta)=2^{k_2}\theta^{2k_1+k_2}(1-\theta)^{k_2+2k_3}$.
• 令 $\displaystyle \frac{\mathrm{d}\ln L(\theta)}{\mathrm{d} \theta}=0$，解得 $\theta=\frac{2k_1+k_2}{2n}$.
• 注意到 $\displaystyle k_1-k_3=-\sum\limits_{i=1}^nx_i$，由此可得 $2k_1+k_2=n+k_1-k_3=n-\sum\limits_{i=1}^nx_i$.
• 综上，$\theta$ 的 MLE 为 $\displaystyle \hat{\theta}_L=\frac12\left(1-\overline{X}\right)$.

---

例 假设某电子器件的寿命 $X$（单位：小时）服从参数为 $\theta$ 的指数分布，现从这批器件中任取了 $n$ 只进行独立寿命试验，试验进行到预定时间 $T$ 时结束，此时恰好有 $k$ 只器件失效，试求 $\theta$ 的MLE.

---

提示：

• $X$ 的密度函数 $f(x;\theta)=\left\{\begin{array}{l}\frac1{\theta}\mathrm{e}^{-\frac{x}{\theta}},& x\geq 0,\\ 0,& \mathrm{其他}.\end{array}\right.$
• 设随机变量 $Y=\left\{\begin{array}{l}1,& \text{器件寿命不超过}T,\\ 0,&\text{其他}.\end{array}\right.$
• $\displaystyle P\{Y=1\}=P\{X\leq T\}=\int_{0}^{T}\frac1{\theta}\mathrm{e}^{-\frac x{\theta}}\mathrm{d}x=1-\mathrm{e}^{-\frac T{\theta}}.$
• $P\{Y=0\}=1-P\{X=1\}=\mathrm{e}^{-\frac T{\theta}}$.
• 似然函数 $\displaystyle L(\theta)=\left(1-\mathrm{e}^{-\frac T{\theta}}\right)^k\left(\mathrm{e}^{-\frac T{\theta}}\right)^{n-k}$.
• 对数似然函数 $\displaystyle \frac{\mathrm{d}\ln L(\theta)}{\mathrm{d}\theta}=\frac{T}{\theta^2}\left(n-k-\frac{k\mathrm{e}^{-\frac T{\theta}}}{1-\mathrm{e}^{-\frac T{\theta}}}\right)$.
• 令 $\displaystyle \frac{\mathrm{d}\ln L(\theta)}{\mathrm{d}\theta}=0$, 解得 $\displaystyle \theta$ 的 MLE 为 $\hat{\theta}=\frac{T}{\ln n-\ln(n-k)}$.

---

6.2.3 参数估计的评判标准

---

一个“好的”估计应该满足什么条件？

1. 无偏性 (Unbiasedness)
   
   • 估计量的波动应以真值 $\theta$ 为中心.
2. 有效性 (Efficiency)
   
   • 估计量与真值的距离总体来说应该较小.
3. 相合性/一致性 (Consistency)
   
   • 估计量的精度随样本容量 $n$ 的增加而不断提高.

---

1. 无偏性

若估计量 $\hat{{\theta}}=\hat{\theta}\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 的数学期望存在，且对任意 $\theta\in\Theta$ 有

$$E(\hat{\theta})=\theta,$$

则称 $\hat{\theta}$ 是 $\theta$ 的 无偏估计 (Unbiased Estimation), 否则称为 有偏估计 (Biased Estimation).

---

例 $X_1, X_2,\ldots, X_n$ 是取自总体 $X$ 的样本, 总体 $X$ 的数学期望 $E(X)=\mu$ 未知, 则下列统计量均为 $\mu$ 的无偏估计:

1. $\hat{\mu}_1=\overline{X}$.
2. $\displaystyle \hat{\mu}_2=\sum\limits_{i=1}^{n}a_iX_i$，其中 $\displaystyle \sum\limits_{i=1}^{n}a_i=1$.
3. $\hat{\mu}_3=X_i,\;i=1,2,...,n$.

---

定理 设 $X_1, X_2, ..., X_n$ 是来自总体 $X$ 的简单随机样本，则

1. 样本均值 $\displaystyle \overline{X}=\frac{1}{n} \sum_{i=1}^{n} X_{i}$ 是总体均值的无偏估计;
2. 修正的样本方差 $\displaystyle \tilde{S}^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2}$ 是总体方差的无偏估计.

---

注：

• 无偏性只有在大量试验的情况下才有意义！
• 若 $E(\hat{\theta})\ne\theta$, 则称 $b(\hat{\theta})=E(\hat{\theta})-\theta$ 为 $\hat{\theta}$ 的 偏差 (Bias).
• 若 $\lim_{n\to\infty}b(\hat{\theta})=0$，则称 $\hat{\theta}$ 是 $\theta$ 的 渐进无偏估计 (Asymptotic Ubiased Estimation).
• 例： $(\overline{X})^2,S^2$ 分别是 $\mu^2$ 和 $\sigma^2$ 的渐进无偏估计.
• 这个例子说明，$\hat{\theta}$ 是 $\theta$ 的无偏估计，不一定能推出 $\hat{\theta}$ 的函数 $g(\hat{\theta})$ 是 $g(\theta)$ 的无偏估计.

---

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim U(0,\theta)$ 的简单随机样本，其中 $\theta>0$ 是未知参数.

1. 试求 $\theta$ 的矩估计 $\hat{\theta}_M$ 与最大似然估计 $\hat{\theta}_L$;
2. $\hat{\theta}_M$ 与 $\hat{\theta}_L$ 是否是 $\theta$ 的无偏估计;
3. 证明 $\hat{\theta}_{2}=(n+1) X_{(1)}$ 是 $\theta$ 的无偏估计.

---

分析：

• $E(X)=\frac{\theta}2$.
• 令 $\overline{X}=\theta / 2$, 解得 $\theta$ 的矩估计为 $\hat{\theta}_{M}=2 \overline{X}$.
• $\displaystyle E\left(\hat{\theta}_{M}\right)=2 E(\overline{X})=2 E(X)=2 \cdot \frac{\theta}{2}=\theta$.
• 故 $\hat{\theta}_{M}$ 是 $\theta$ 的无偏估计.

---

• 似然函数 $\displaystyle L(\theta)=\frac{1}{\theta^{n}}\left(0<X_{1}, \cdots, X_{n}<\theta\right)$.
• $\theta$ 的 MLE 为 $\displaystyle \hat{\theta}_{L}=X_{(n)}=\max _{1 \leq i \leq n} X_{i}$.
• $X_{(n)}$ 的密度函数 $f_{\max }(z)=\left\{\begin{array}{ll} n \dfrac{1}{\theta}\left(\dfrac{z}{\theta}\right)^{n-1}, &0<z<\theta \\ {0,} & {\text {其他}}\end{array}\right.$.
• $\displaystyle E\left(\hat{\theta}_{L}\right) =\int_{0}^{\theta} z \cdot n \frac{1}{\theta}\left(\frac{z}{\theta}\right)^{n-1} \mathrm{d} z=\frac{n}{n+1} \theta<\theta$.
• 由此可知 $\hat{\theta}_{L}=X_{(n)}$ 是 $\theta$ 的有偏估计.
• 经修正后，$\displaystyle \hat{\theta}=\frac{n+1}{n} \hat{\theta}_{L}=\frac{n+1}{n} X_{(n)}$ 是 $\theta$ 的无偏估计.

---

军力评估问题

例 在“二战”中, 盟军在多个战场缴获德军共计 $50$ 辆虎式坦克. 这些坦克都带有数字编号, 假定坦克编号 $x_1,x_2,...,x_{50}$ 在 $\{1,2,...,N\}$ 上的等可能取值, 问如何估计虎式坦克总数 $N$？

1. 矩估计：$\hat{N}_M=2\overline{x}-1$.
2. 极大似然估计：$\hat{N}_L=x_{\max}$.
3. 修正的 MLE：$\displaystyle \hat{N}'_{L}=\frac{n+1}{n} x_{\max}$.

---

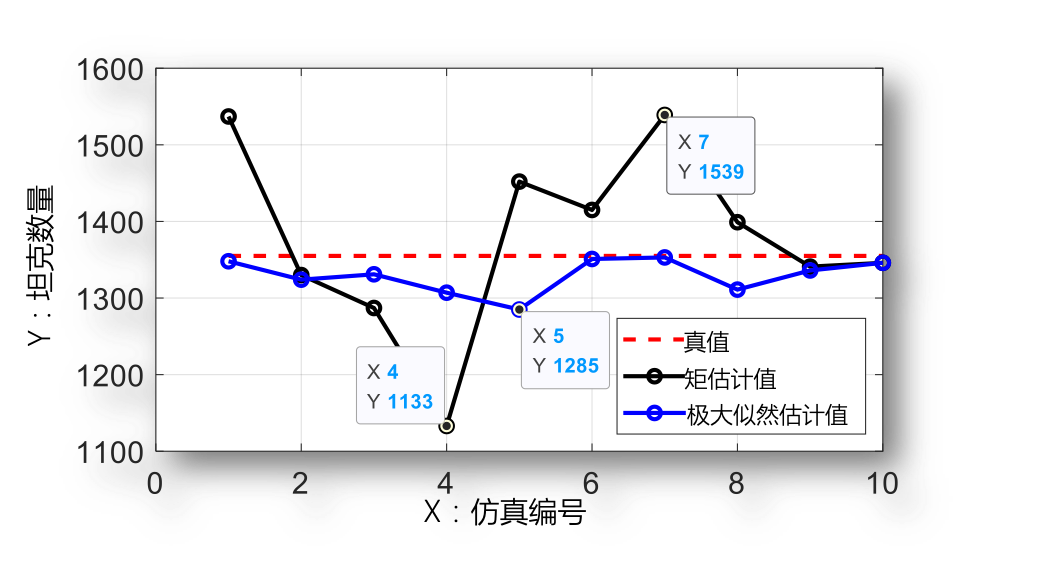
取真值 $1355$，$10$ 次仿真的结果显示，修正的 MLE 具有最好的精确度和稳定性.

---

2. 有效性

若估计量 $\hat{{\theta}}=\hat{\theta}\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 的方差存在，称

$$r(\hat{\theta})=E\left[(\hat{\theta}-\theta)^2\right]$$

为估计量 $\hat{\theta}$ 的 均方误差 (Mean Square Error, MSE).

• 若存在 $\theta$ 的一个估计量 $\hat{\theta}^*$，使得对 $\theta$ 的任意估计量 $\hat{\theta}$，都有 $r(\hat{\theta}^*)\leq r(\hat{\theta})$，则称 $\hat{\theta}^*$ 是 $\theta$ 的 最小均方误差估计 (MMSEE).

---

估计量的“波动”与“偏差”

• 系统误差(System Error) $b(\hat{\theta})=E(\hat{\theta})-\theta$.
  
  • 反映了估计量的波动中心与真值的差异.
• 绝对误差(Absolute Error) $r(\hat{\theta})=E\left[(\hat{\theta}-\theta)^{2}\right]$.
  
  • 反映了估计量与真值的均方误差.

• 随机误差(Random Error) $D(\hat{\theta})=E\left[(\hat{\theta}-E(\hat{\theta}))^{2}\right]$.

  • 反映了估计量自身的波动.

• 定理 $r(\hat{\theta})=D(\hat{\theta})+[b(\hat{\theta})]^{2}$.

• 推论 若 $\hat{\theta}$ 是 $\theta$ 的无偏估计，则方差小的估计量应该更有效.

---

定理证明：

• $E[\hat{\theta}-E(\hat{\theta})]=E(\hat{\theta})-E(\hat{\theta})=0$
• $r(\hat{\theta})=E\left[(\hat{\theta}-\theta)^{2}\right]$
  
  • $=E\left\{[(\hat{\theta}-E(\hat{\theta}))-(\theta-E(\hat{\theta}))]^{2}\right\}$
  • $=E\left[(\hat{\theta}-E(\hat{\theta}))^{2}\right]+E\left[(\theta-E(\hat{\theta}))^{2}\right]-2 E(\hat{\theta}-E(\widehat{\theta}))(\theta-E(\widehat{\theta}))$
  • $=D(\widehat{\theta})+(\theta-E(\widehat{\theta}))^{2}=D(\widehat{\theta})+[b(\widehat{\theta})]^{2}$

---

无偏估计的有效性

设 $\hat{\theta}_{1}, \hat{\theta}_{2}$ 均为 $\theta$ 的无偏估计量，若

$$D\left(\hat{\theta}_{1}\right)<D\left(\hat{\theta}_{2}\right)$$

则称估计量 $\hat{\theta}_{1}$ 较 $\hat{\theta}_{2}$ 更为 有效.

---

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim \mathrm{Exp}(\theta)$ 的简单随机样本.

1. 证明 $\overline{X}, n X_{(1)}$ 都是 $\theta$ 的无偏估计;
2. 判断 $\overline{X}, n X_{(1)}$ 哪个更有效.

---

分析

• 总体 $X$ 的密度函数 $\displaystyle f(x ; \theta)=\left\{\begin{array}{ll}{\frac{1}{\theta} e^{-\frac{x}{\theta}},} & {x>0} \\ {0,} & {x \leq 0}\end{array},(\theta>0)\right.$.
• $E(\overline{X})=E(X)=\theta$，故 $\overline{X}$ 是 $\theta$ 的无偏估计.
• $\displaystyle X_{(1)}\sim\mathrm{Exp}\left(\frac{\theta}{n}\right)$, 密度函数 $\displaystyle f_{(1)}(x)=\left\{\begin{array}{l}\frac{n}{\theta}\mathrm{e}^{-\frac{n}{\theta}x},& x\geq 0\\ 0,& \text{其他}\end{array}\right.$.
• 由此可得 $\displaystyle E(nX_{(1)})=n\cdot\frac{\theta}n=\theta$, 故 $nX_{(1)}$ 也是 $\theta$ 的无偏估计.

---

• $D(X)=\theta^2$.
• $\displaystyle D(\overline{X})=D\left(\frac{1}{n} \sum_{i=1}^{n} X_{i}\right)=\frac{D(X)}{n}=\frac{\theta^{2}}{n}$.
• $\displaystyle D(X_{(1)})=\frac{\theta^2}{n^2}$.
• $D(nX_{(1)})=n^2D(X_{(1)})=\theta^2$.
• 由此可见 $\overline{X}$ 作为 $\theta$ 的估计，相对于 $nX_{(1)}$ 更有效.

---

最小方差无偏估计（MVUE）

设 $\hat{\theta}^{*}$ 是未知参数 $\theta$ 的无偏估计量，若对 $\theta$ 的任一无偏估计量 $\hat{\theta}$ 有

$$D\left(\hat{\theta}^{*}\right) \leq D(\hat{\theta}),$$

则称无偏估计量 $\hat{\theta}^{*}$ 是 $\theta$ 的 最小方差无偏估计 (Minimum Variance Unbiased Estimate).

---

Cramér–Rao 下界

设总体 $X$ 的密度函数为 $f(x;\theta)$，$X_1, X_2, ..., X_n$ 是来自总体 $X$ 的简单随机样本，$g(\theta)$ 为待估变量，其中 $\theta\in\Theta$ 是未知参数，统计量 $\hat{g}=\hat{g}\left(X_{1}, X_{2}, \ldots, X_{n}\right)$ 是 $g(\theta)$ 的无偏估计.

• 问： $\hat{g}$ 有没有可能完美地逼近 $g(\theta)$？
  
  • 即：是否可能 $D(\hat{g})=0$？
• 不可能！给定样本容量，无偏估计的方差存在非零下界！

---

记 $\boldsymbol{X}=(X_1,X_2,...,X_n)$，$\boldsymbol{x}=(x_1,x_2,...,x_n)$，$\mathrm{d}\boldsymbol{x}=\mathrm{d}x_1\mathrm{d}x_2...\mathrm{d}x_n$

定理 设 $E[\hat{g}\left(\boldsymbol{X}\right)]=g(\theta)$，$f(x;\theta)$ 为总体 $X$ 的密度函数，$L(\theta)$ 为似然函数，若

1. $\displaystyle I(\theta) = E\left[\left(\frac{\partial}{\partial \theta} \ln f(X ; \theta)\right)^{2}\right]>0$.
2. $\displaystyle \frac{\partial}{\partial \theta} f(x ; \theta)$ 几乎处处存在，且 $\displaystyle \int_{\mathbb{R}} \frac{\partial}{\partial \theta} f(x ; \theta) \mathrm{d} x=\frac{\partial}{\partial \theta}\int_{\mathbb{R}} f(x ; \theta) \mathrm{d} x=0$.

3. $\displaystyle \frac{\partial g(\theta)}{\partial \theta}$ 几乎处处存在，且 $\displaystyle \frac{\partial}{\partial \theta}\int_{\mathbb{R}^n} \hat{g}(\boldsymbol{x})\cdot L(\theta) \mathrm{d} \boldsymbol{x}=\int_{\mathbb{R}^n} \hat{g}(\boldsymbol{x})\cdot\frac{\partial L(\theta)}{\partial \theta}\mathrm{d} \boldsymbol{x}.$

   • 则 $\displaystyle D\left(\hat{g}(\boldsymbol{X})\right) \geq \frac{\left[g^{\prime}(\theta)\right]^{2}}{n I(\theta)}$.

---

证明：

• $\boldsymbol{X}$ 的联合密度 $\displaystyle f(\boldsymbol{x};\theta)=\prod\limits_{i=1}^nf(x_i;\theta)$.
• $\displaystyle g'(\theta)=\dfrac{\partial}{\partial\theta}E[\hat{g}(\boldsymbol{X})]=\dfrac{\partial}{\partial\theta}\int_{\mathbb{R}^n}\hat{g}(\boldsymbol{x})f(\boldsymbol{x};\theta)\mathrm{d}\boldsymbol{x}$
  
  • $\displaystyle \stackrel{3.}{=}\int_{\mathbb{R}^n}\hat{g}(\boldsymbol{x})\dfrac{\partial}{\partial\theta}f(\boldsymbol{x};\theta)\mathrm{d}\boldsymbol{x}=\int_{\mathbb{R}^n}\hat{g}(\boldsymbol{x})\dfrac{\partial \ln f(\boldsymbol{x};\theta)}{\partial\theta}f(\boldsymbol{x};\theta)\mathrm{d}\boldsymbol{x}$
  • $\displaystyle =E\left[\hat{g}(\boldsymbol{X})\dfrac{\partial \ln f(\boldsymbol{X};\theta)}{\partial\theta}\right]$

---

• $E\left[\dfrac{\partial \ln f(\boldsymbol{X};\theta)}{\partial\theta}\right]=E\left[\dfrac{\partial}{\partial\theta}\sum\limits_{i=1}^n\ln f(X_i;\theta)\right]=\sum\limits_{i=1}^nE\left[\dfrac{\partial\ln f(X_i;\theta)}{\partial\theta}\right]$
  
  • $\displaystyle =\sum\limits_{i=1}^n\int_{\mathbb{R}}\dfrac{\partial\ln f(x)}{\partial\theta}f(x;\theta)\mathrm{d}x=n\int_{\mathbb{R}}\dfrac{\partial f(x;\theta)}{\partial\theta}\mathrm{d}x\stackrel{2.}{=}0$
• ${D\left(\dfrac{\partial \ln f(\boldsymbol{X};\theta)}{\partial\theta}\right)}=\sum\limits_{i=1}^nD\left[\dfrac{\partial \ln f(X_i;\theta)}{\partial\theta}\right]=nD\left[\dfrac{\partial \ln f(X;\theta)}{\partial\theta}\right]$
  
  • $=nE\left[\left(\dfrac{\partial \ln f(X;\theta)}{\partial\theta}\right)^2\right]=nI(\theta)$

---

• $g'(\theta)=E\left[\hat{g}(\boldsymbol{X})\dfrac{\partial \ln f(\boldsymbol{X};\theta)}{\partial\theta}\right]$
  
  • $=E\left[\hat{g}(\boldsymbol{X})\dfrac{\partial \ln f(\boldsymbol{X};\theta)}{\partial\theta}\right]-E\left[\hat{g}(\boldsymbol{X})\right]E\left[\dfrac{\partial \ln f(\boldsymbol{X};\theta)}{\partial\theta}\right]$
  • $=\mathrm{Cov}\left[\hat{g}(\boldsymbol{X}),\dfrac{\partial \ln f(\boldsymbol{X};\theta)}{\partial\theta}\right]\qquad\qquad$ (Cauchy-Schwarz 不等式)
  • $\leq\sqrt{D(\hat{g}(\boldsymbol{X}))}\sqrt{D\left(\dfrac{\partial \ln f(\boldsymbol{X};\theta)}{\partial\theta}\right)}\leq\sqrt{D(\hat{g}(\boldsymbol{X}))}\sqrt{nI(\theta)}$
• 整理后即得 $D(\hat{g}(\boldsymbol{X}))\geq\dfrac{[g'(\theta)]^2}{nI(\theta)}$.

---

Cramér–Rao 下界

$$D\left(\hat{g}\right) \geq \frac{\left[g^{\prime}(\theta)\right]^{2}}{n I(\theta)}.$$

• $\displaystyle \frac{\left[g^{\prime}(\theta)\right]^{2}}{n I(\theta)}$ 称为无偏估计量的 Cramér–Rao 下界 (C-R 下界).
• $\displaystyle \bbox[lightgreen]{I(\theta) = E\left[\left(\frac{\partial}{\partial \theta} \ln f(X ; \theta)\right)^{2}\right]}$ 称为 Fisher 信息(量).[^2]
• 例：未知参数 $\theta$ 的任意无偏估计（相当于取 $g(\theta)=\theta$）的 C-R 下界为 $\displaystyle \frac{1}{nI(\theta)}$.

---

Fisher 信息

• C-R 下界的存在，意味着统计量对参数的估计能力是有限的，由待估参数的形式、分布的 Fisher 信息和样本容量共同决定.
• Wikipedia: The Fisher information is a way of measuring the amount of information that an observable random variable $X$ carries about an unknown parameter $\theta$ of a distribution that models $X$.
• 对于要估计的参数，采样的数据量越大，意味着数据提供的信息量越大，从而 C-R 下界就越小，那么就能越准确地估计出该参数的值.

---

推论 在前述定理条件下，若还有 $\displaystyle \int_{-\infty}^{+\infty}\frac{\partial^2}{\partial\theta^2}f(x;\theta)\mathrm{d}x=\frac{\partial^2}{\partial\theta^2}\int_{-\infty}^{+\infty}f(x;\theta)\mathrm{d}x=0$，则

$$\displaystyle I(\theta)=-E\left[\frac{\partial^2}{\partial\theta^2}\ln f(X;\theta)\right]$$

---

证明思路

• $\displaystyle 0=\int_{\mathbb{R}}\dfrac{\partial^2}{\partial\theta^2}f(x;\theta)\mathrm{d}x=\int_{\mathbb{R}}\dfrac{\partial}{\partial\theta}\left[\dfrac{\partial\ln f(x;\theta)}{\partial\theta}f(x;\theta)\right]\mathrm{d}x$
  
  • $\displaystyle =\int_{\mathbb{R}}\dfrac{\partial^2\ln f(x;\theta)}{\partial\theta^2}f(x;\theta)\mathrm{d}x+\int_{\mathbb{R}}\left[\dfrac{\partial\ln f(x;\theta)}{\partial\theta}\right]^2f(x;\theta)\mathrm{d}x$
  • $\displaystyle =E\left[\dfrac{\partial^2\ln f(X;\theta)}{\partial\theta^2}\right]+E\left[\left(\dfrac{\partial\ln f(X;\theta)}{\partial\theta}\right)^2\right]$
  • $\displaystyle =E\left[\dfrac{\partial^2\ln f(X;\theta)}{\partial\theta^2}\right]+I(\theta)$

---

例：均匀分布参数的 C-R 下界

求均匀分布 $U(0,\theta)$ 中未知参数 $\theta$ 的无偏估计的 C-R 下界.

• 提示：$U(0,\theta)$ 的密度 $f(x;\theta)=\left\{\begin{array}{cc}\frac{1}{\theta}, & 0<x<\theta\\ 0, & \text{其他}\end{array}\right.$
• $I(\theta)=E\left[\left(\frac{\partial}{\partial \theta} \ln f(X ; \theta)\right)^{2}\right]=\int_0^{\theta}\frac{1}{\theta^2}f(x;\theta)\mathrm{d}x=\frac{1}{\theta^2}.$
• 故 $\theta$ 的无偏估计的 C-R 下界为 $\frac{1}{nI(\theta)}=\frac{\theta^2}{n}$.

---

讨论

• $U(0,\theta)$ 中参数 $\theta$ 的函数 $g(\theta)=\dfrac{\theta}{2}$ 的无偏估计的 C-R 下界为 $\dfrac{[g'(\theta)]^2}{nI(\theta)}=\dfrac{\theta^2}{4n}.$
• 注意到 $\hat{g}(X_1,...,X_n)=\overline{X}$ 是 $g(\theta)=\dfrac{\theta}{2}$ 的无偏估计，
  
  • 但 $D(\hat{g})=D(\overline{X})=\dfrac{D(X)}{n}=\dfrac{\theta^2}{12n}<\dfrac{\theta^2}{4n}.$
• 这就与定理结论相矛盾了！
• 造成这一问题的原因是什么？

---

事实上，$U(0,\theta)$ 的密度函数不满足 C-R 下界的条件2：

$$\int_{\mathbb{R}}\dfrac{\partial}{\partial\theta}f(x;\theta)\mathrm{d}x=\dfrac{\mathrm{d}}{\mathrm{d}\theta}\int_{\mathbb{R}}f(x;\theta)\mathrm{d}x=0.$$

• 本例中，$\int_{\mathbb{R}}\dfrac{\partial}{\partial\theta}f(x;\theta)\mathrm{d}x=\int_0^{\theta}\dfrac{\partial}{\partial\theta}\left(\dfrac{1}{\theta}\right)\mathrm{d}x=-\dfrac{1}{\theta}\ne 0.$
• 所以，结论是因为 $U(0,\theta)$ 这个总体不满足 C-R 下界的条件，因此导致了以上相互矛盾的结果.

---

证明某个统计量是未知參数的 MVUE 的一般过程

1. 证明估计量 $\hat{\theta}$ 是 $\theta$ 的无偏估计量;
2. 计算估计量 $\hat{\theta}$ 的方差 $D(\hat{\theta})$;
3. 计算 Fisher 信息量 $I(\theta)$;

4. 若 $\displaystyle D(\hat{\theta})=\frac{1}{n I(\theta)}$，则$\hat{\theta}$ 是 $\theta$ 的 MVUE.

   • 注：有时候，C-R 下界是无法达到的.
   • 例如：对于 $X\sim N(\mu,\sigma^2)$，$\tilde{S}^2$ 是 $\sigma^2$ 的 MVUE.
   • 但是，$\displaystyle D\left(\widetilde{S}^{2}\right)=\frac{2 \sigma^{4}}{n-1}>\frac{2 \sigma^{4}}{n}=\frac{1}{n I\left(\sigma^{2}\right)}$.

---

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim N(\mu,\sigma^2)$ 的简单随机样本，证明 $\overline{X}$ 是 $\mu$ 的 MVUE.

• 提示：$X$ 的密度函数：$\displaystyle f\left(x ; \mu, \sigma^{2}\right)=\frac{1}{\sqrt{2 \pi} \sigma} \mathrm{e}^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}$.
• $\displaystyle \ln f\left(x ; \mu, \sigma^{2}\right)=-\ln \sqrt{2 \pi}-\frac{1}{2} \ln \sigma^{2}-\frac{(x-\mu)^{2}}{2 \sigma^{2}}$.
• $\displaystyle I(\mu)=E\left[\left(\frac{\partial \ln f\left(X ; \mu, \sigma^{2}\right)}{\partial \mu}\right)^{2}\right]=E\left[\left(\frac{X-\mu}{\sigma^{2}}\right)^{2}\right]=\frac{1}{\sigma^{4}} E\left[(X-\mu)^{2}\right]=\frac{D(X)}{\sigma^{4}}=\frac{1}{\sigma^{2}}$.
• $\mu$ 的无偏估计的 C-R 下界为 $\displaystyle \frac{1}{n I(\mu)}=\frac{\sigma^{2}}{n}$.
• $\displaystyle D(\overline{X})=\frac{\sigma^{2}}{n}$，由此可知 $\overline{X}$ 就是 $\mu$ 的 MVUE.

---

例 设 $X_1, X_2, ..., X_n$ 是来自总体 $X\sim \mathrm{Exp}(\theta)$ 的简单随机样本，总体 $X$ 的密度函数为

$$f(x ; \theta)=\left\{\begin{array}{ll}{\frac{1}{\theta} e^{-\frac{x}{\theta}},} & {x>0} \\ {0,} & {x \leq 0}\end{array},(\theta>0)\right.$$

证明 $\overline{X}$ 是 $X$ 的最小方差无偏估计.

• 提示：$\displaystyle \ln f(x ; \theta)=-\ln\theta-\frac x{\theta}$.
• $\displaystyle \left(\frac{\mathrm{d}\ln f(x ; \theta)}{\mathrm{d}\theta}\right)^2=\frac{x^2}{\theta^4}-2\frac{x}{\theta^3}+\frac{1}{\theta^2}$.
• $\displaystyle I(\theta)=\frac{E(X^2)}{\theta^4}-2\frac{E(X)}{\theta^3}+\frac{1}{\theta^2}=\frac{1}{\theta^2}$.
• $\displaystyle D(\overline{X})=\frac{\theta^2}{n}$.

---

优效估计

设 $\hat{g}(X_1,X_2,\ldots,X_n)$ 是待估参数 $g(\theta)$ 的一个无偏估计量.

• $\displaystyle e(\hat{g})=\frac{[g'(\theta)]^2}{nI(\theta)}\bigg/D(\hat{g})$ 称为 $\hat{g}$ 的 估计效率 (Estimation Efficiency).
• 如果 $e(\hat{g})=1$，则称 $\hat{g}$ 是 $g$ 的 优效（完全高效）估计 (Optimal Estimation).
• 如果 $\hat{g}$ 满足 $\displaystyle \lim_{n\to\infty}e(\hat{g})=1$，则称 $\hat{g}$ 为 $g$ 的 渐进优效估计 (Asmptotic Optimal Estimation).
• 例：对于正态总体 $N(\mu,\sigma^2)$，$\tilde{S}^2$ 是 $\sigma^2$ 的渐进优效估计.

---

例 设 $X_1,X_2,\ldots,X_n$ 是取自总体 $U(0,\theta)$ 的简单随机样本 ($\theta>0$ 未知). 试以均方误差的大小为准则，比较 $\theta$ 的估计 $2\overline{X},\;X_{(n)}$ 和 $\displaystyle \frac{n+1}{n}X_{(n)}$ 中哪一个较优？

---

提示：

• $E(2\overline{X})=2E(\overline{X})=\theta$，故 $2\overline{X}$ 是 $\theta$ 的无偏估计，即 $b(2\overline{X})=0$.
• $\displaystyle D(X_i)=\frac{\theta^2}{12},\;i=1,2,...,n$.
• $\displaystyle D(2 \overline{X})=\frac{4}{n^{2}} \sum_{i=1}^{n} D\left(X_{i}\right)=\frac{\theta^{2}}{3 n}$.
• 故 $\displaystyle r(2 \overline{X})=D(2 \overline{X})+b^2(2\overline{X})=\frac{\theta^{2}}{3 n}$.

---

• $E(X_{(n)})=\frac{n}{n+1}\theta$，故 $X_{(n)}$ 是 $\theta$ 的有偏估计.
• $\displaystyle b\left(X_{(n)}\right)=E\left(X_{(n)}\right)-\theta=-\frac{\theta}{n+1}$.
• $\displaystyle E\left(X_{(n)}^{2}\right)=\int_{0}^{\theta} x^{2} \frac{n x^{n-1}}{\theta^{n}} \mathrm{d} x=\frac{n}{n+2} \theta^{2}$.
• $\displaystyle D\left(X_{(n)}\right)=E\left(X_{(n)}^{2}\right)-\left[E\left(X_{(n)}\right)\right]^{2}=\frac{n}{n+2} \theta^{2}-\left(\frac{n \theta}{n+1}\right)^{2}$.
• 故 $\displaystyle r\left(X_{(n)}\right)=D\left(X_{(n)}\right)+\left[b\left(X_{(n)}\right)\right]^{2}=\frac{2 \theta^{2}}{(n+1)(n+2)}$.

---

• $\displaystyle\frac{n+1}{n} X_{(n)}$ 是 $\theta$ 的无偏估计，$\displaystyle b\left(\frac{n+1}{n} X_{(n)}\right)=0$.
• $\displaystyle r\left(\frac{n+1}{n} X_{(n)}\right)=D\left(\frac{n+1}{n} X_{(n)}\right)+b^2\left(\frac{n+1}{n} X_{(n)}\right)=\frac{(n+1)^{2}}{n^{2}} D\left(X_{(n)}\right)=\frac{\theta^{2}}{n(n+2)}$.
• $n\geqslant2$ 时,
  
  • $\displaystyle r\left(\frac{n+1}{n} X_{(n)}\right)=\frac{\theta^{2}}{n(n+2)}<\min\left\{\frac{\theta^{2}}{3 n},\frac{2 \theta^{2}}{(n+1)(n+2)}\right\}=\min\left\{r(2 \overline{X}),r\left(X_{(n)}\right)\right\}.$
• 综上，给定的三个估计量中 $\displaystyle\frac{n+1}{n}X_{(n)}$ 最有效.

---

3. 相合性

设 $\hat{\theta}_{n}=\hat{\theta}\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 是未知参数 $\theta$ 的点估计，若对任意 $\varepsilon>0$，有

$$\lim\limits_{n \rightarrow \infty} P\left\{\left|\hat{\theta}_{n}-\theta\right| \geq \varepsilon\right\}=0,$$

则称 $\hat{\theta}_{n}$ 是 $\theta$ 的 相合估计 (Consistent Estimator).

• 随着 $n$ 的增加, 估计量与参数真值的绝对偏差较大的可能性越来越小.
• 由 Khinchin 大数定律可知，样本 $k$ 阶矩是总体 $k$ 阶矩的相合估计量，因此矩估计量一般是相合估计量.

---

无偏估计必是相合估计吗？

• 不一定！
  
  • 无偏性只能说明估计的中心与真值一致，但估计值的分布仍然可能比较分散；
  • 相合性则能保证随着 $n$ 的增大，估计值越来越像真值.
• 相合估计一定是无偏估计吗？
  
  • 不一定，但相合估计一定是渐进无偏估计！

---

Chebyshev 不等式

设 $g(X)$ 是随机变量 $X$ 的非负连续函数，如果 $E[g(X)]$ 存在，则对于任一正常数 $c$，均有

$$P\{g(X) \geqslant c\} \leqslant \frac{E[g(X)]}{c}.$$

证明：

$$E[g(X)]=\displaystyle\int_{-\infty}^{+\infty} g(x) f(x) \mathrm{d} x\geqslant \int_{\{ x| g(x) \geqslant c\}} g(x) f(x) \mathrm{d} x\\ \geqslant c \displaystyle\int_{\{x | g(x) \geqslant c)} f(x) \mathrm{d} x=c P\{g(X) \geqslant c\}$$

• 推论 若随机变量 $X$ 的期望和方差存在，则对任意 $\varepsilon>0$，总有

$$\bbox[yellow]{P\left\{|X-E(X)|\geq\varepsilon\right\}\leq\dfrac{D(X)}{\varepsilon^2}}$$

---

相合估计的判定

设 $\hat{\theta}=\hat{\theta}\left(X_{1}, X_{2}, \cdots, X_{n}\right)$ 是未知参数 $\theta$ 的估计量，

• $P\left\{\left|\widehat{\theta}-\theta\right| \geqslant \varepsilon\right\}=P\left\{\left|\widehat{\theta}-\theta\right|^2 \geqslant \varepsilon^2\right\}\leqslant\dfrac{1}{\varepsilon^2}E\left[(\hat{\theta}-\theta)^2\right]=\dfrac{r(\hat{\theta})}{\varepsilon^2}$.

• 如果 $\lim\limits_{n\to\infty}r(\hat{\theta})=0$，则 $\hat{\theta}$ 是 $\theta$ 的相合估计.

• 特别地，若 $\hat{\theta}$ 是无偏估计，则 $P\left\{\left|\hat{\theta}-\theta\right|\geqslant\varepsilon\right\}\leqslant\dfrac{D(\hat{\theta})}{\varepsilon^2}$.

---

定理 无论总体 $X$ 服从什么分布，若

$$\mu \triangleq E(X), \quad\sigma^{2} \triangleq D(X)$$

都存在，则

1. 样本均值 $\overline{X}$ 是总体均值 $\mu$ 的相合估计；
2. 样本方差 $S^2$ 与修正的样本方差 $\tilde{S}^2$ 都是总体方差 $\sigma^2$ 的相合估计.

---

证明思路

• 样本均值 $\overline{X}$ 是总体均值 $\mu$ 的无偏估计.
• 对任意 $\varepsilon>0$，由 Chebyshev 不等式,
  
  • $P\{|\overline{X}-\mu| \geqslant \varepsilon\} \leqslant \dfrac{D(\overline{X})}{\varepsilon^{2}}=\dfrac{\sigma^{2}}{n \varepsilon^{2}}$.
• 因此 $\lim\limits_{n \to+\infty} P\{|\overline{X}-\mu| \geqslant \varepsilon\}=0$, 故样本均值 $\overline{X}$ 是总体均值 $\mu$ 的相合估计.

---

• 修正的样本方差 $\tilde{S}^2$ 是总体方差 $\sigma^2$ 的无偏估计.
• $P\left\{\left|\tilde{S}^{2}-\sigma^{2}\right| \geqslant \varepsilon\right\} \leqslant \dfrac{D\left(\tilde{S}^{2}\right)}{\varepsilon^{2}}$.
• 当 $n$ 充分大时， $\dfrac{(n-1) \tilde{S}^{2}}{\sigma^{2}}$ 近似服从 $\chi^{2}(n-1)$.
• 故 $D\left(\dfrac{(n-1) \tilde{S}^{2}}{\sigma^{2}}\right)=2(n-1)$，进而可得 $D\left(\tilde{S}^{2}\right)=\dfrac{2 \sigma^{4}}{n-1}$.
• 综上，由夹逼准则 $\lim\limits_{n \to\infty} P\left\{\left|\tilde{S}^{2}-\sigma^{2}\right| \geqslant \varepsilon\right\}=0$.

---

非正态总体的极限分布[2]

设 $X_1,X_2,\ldots,X_n$ 为来自总体 $X$ 的简单随机样本，$E(X)=\mu,D(X)=\sigma^2$ 均存在，则当 $n$ 充分大时：

1. $\overline{X}_n$ 近似服从 $N\left(\mu,\dfrac{\sigma^2}{n}\right)$.
2. $\sqrt{n}\dfrac{\overline{X}_n-\mu}{\tilde{S}_n}$ 近似服从 $N(0,1)$.

---

例 设总体 $X$ 服从 $(0,\theta)$ 上的均匀分布，其中 $\theta>0$ 未知，证明 $\theta$ 的 MLE $X_{(n)}$ 是相合估计量.

提示：

• $X_{(n)}$ 是 $\theta$ 的有偏估计.
• $P\left\{\left|X_{(n)}-\theta\right| \geqslant \varepsilon\right\} \leqslant \dfrac{r\left(X_{(n)}\right)}{\varepsilon^{2}}=\dfrac{2 \theta^{2}}{(n+1)(n+2) \varepsilon^{2}}.$
• 因此 $\lim\limits_{n \rightarrow+\infty} P\left\{\left|X_{(n)}-\theta\right| \geqslant \varepsilon\right\}=0$, 即 $X_{(n)}$ 是 $\theta$ 的相合估计量.

---

6.2.4 Bayes 估计

---

统计的经典学派与 Bayes 学派

• 经典学派 的统计推断主要依赖于
  
  • 样本信息 抽取样本所得观测值所提供的信息.
  • 总体信息 总体的分布或总体所属的分布族.
    
    • 例如：总体为正态分布、总体的密度函数关于均值对称、总体的前两阶矩均存在.
• Bayes 学派 认为利用先验信息可以使统计推断更具合理性.
  
  • 先验信息 抽样(试验)之前关于统计问题的一些信息.
    
    • 例如：过去一段时间的产品合格率、总体均值的分布.

---

先验分布

例 每天抽检 $n$ 件产品以确定质量是否满足要求. 产品质量可用不合格品率 $p$ 来度量，也可用 $n$ 件产品中的不合格品件数 $\theta$ 表示.

• 由于生产过程有连续性，可以认为每天的产品质量是有关联的.
• 在估计现在的 $p$ 时，以前积累的资料应该能提供帮助.
• 积累的历史资料就是 先验信息.
• 例如：经过一段时间后，可以对过去 $n$ 件产品中的不合格品件数 $\theta$ 构造一个分布: $P\{\theta=i\}=p_i,\;(i=1,2,...,n)$.
• 对先验信息进行加工所获得的分布称为 先验分布 (Prior Distribution).

---

Bayes 学派

• 任一未知量 $\theta$ 都可以看作随机变量，从而可用一个概率分布（先验分布）去描述.
• 获得样本后，将总体分布、样本与先验分布通过 Bayes 公式结合起来，可得到一个关于未知量 $\theta$ 的新分布，称为 后验分布 (Posterior Distribution).
• 任何关于 $\theta$ 的统计推断都应该基于 $\theta$ 的后验分布进行.
• 例如：在求参数 $\theta$ 的点估计时，可以取其基于后验分布的期望值、最大值或者中位数.
• 如何利用各种先验信息合理地确定先验分布，是 Bayes 估计中的关键问题.

---

Bayes 公式的概率函数形式

设 $\boldsymbol{X}=\{X_1,X_2,...,X_n\}$ 为样本，$\theta$ 为未知参数，则

$$p(\theta|\boldsymbol{X})=\frac{p(\boldsymbol{X}|\theta)p(\theta)}{p(\boldsymbol{X})}.$$

• $p(\theta|\boldsymbol{X})$：$\theta$ 的后验概率函数.[3]
• $p(\boldsymbol{X}|\theta)$：$\theta$ 取定为某个值时的条件概率函数.
• $p(\theta)$：$\theta$ 的先验概率函数.
• $p(\boldsymbol{X})$：$\boldsymbol{X}$ 的边缘概率函数.

---

Bayes 估计

由后验分布 $p(\theta|\boldsymbol{X})$ 估计 $\theta$ 有三种常用的方法.

1. 最大后验估计 使用后验分布概率函数的最大值点作为 $\theta$ 的点估计.
2. 后验中位数估计 使用由后验分布概率函数确定的中位数作为 $\theta$ 的点估计.
3. 后验期望估计 使用由后验分布概率函数确定的均值(期望)作为 $\theta$ 的点估计.

---

例：成功率的估计

设事件 $A$ 在一次试验中发生的概率为 $\theta$，为估计 $\theta$，对试验进行了 $n$ 次独立观测，其中事件 $A$ 发生了 $X$ 次. 试给出 $\theta$ 估计值.

• 提示： $\theta$ 的矩估计和最大似然估计均为 $\hat{\theta}_L=\frac{X}{n}$.

---

Bayes 方法

• 解： 显然 $X|\theta\sim b(n,\theta)$，于是 $p(x|\theta)=P\{X=x|\theta\}=\binom{n}{x}\theta^x(1-\theta)^{n-x},\;x=0,1,...,n$.
• 基于 同等无知原则，假设 $\theta$ 的先验分布为 $U(0,1)$，即 $p(\theta)=\begin{cases} 1, & 0<\theta<1 \\ 0, & \text{其他}\end{cases}$
• 于是 $X$ 与 $\theta$ 的联合概率函数
  
  • $p(x,\theta)=p(x|\theta)p(\theta)=\left\{\begin{array}{cc}\displaystyle\binom{n}{x}\theta^x(1-\theta)^{n-x}, & x=0,1,...,n, 0<\theta<1\\ 0, & \text{其他}\end{array}\right.$

---

• $X$ 的边缘概率函数
  
  • $p(x)=\int_{-\infty}^{+\infty}p(x,\theta)\mathrm{d}\theta=\binom{n}{x}\int_0^1\theta^x(1-\theta)^{n-x}\mathrm{d}\theta$
    
    • $=\displaystyle\binom{n}{x}\dfrac{\Gamma(x+1)\Gamma(n-x+1)}{\Gamma(n+2)}$.
• 于是 $\theta$ 的后验概率函数
  
  • $p(\theta|x)=\dfrac{p(x,\theta)}{p(x)}=\dfrac{\Gamma(n+2)}{\Gamma(x+1)\Gamma(n-x+1)}\theta^{x}(1-\theta)^{n-x},\;0<\theta<1$.
• 即 $\theta|x\sim Be(x+1,n-x+1)$.

---

使用 $\theta$ 的后验期望估计得到

$$\hat{\theta}_B=E(\theta|x)=\frac{x+1}{n+2}.$$

• 例 通过抽检考察产品的不合格率 $\theta$

  • 抽检 $3$ 个均合格：$\hat{\theta}_M=0,\;\hat{\theta}_B=\frac{1}{5}$.
  • 抽检 $10$ 个均合格：$\hat{\theta}_M=0,\;\hat{\theta}_B=\frac{1}{12}$.

• Bayes 估计的结果能够反映出两次抽样的差异，在该场合下相对于最大似然估计更具合理性.

---

6.2.5 区间估计

---

区间估计 (Interval Estimation)

• 参数的点估计，能够给出未知参数的近似值.
• 但在很多实际问题中，更加关心的是参数的取值范围.
• 区间估计：根据样本数据，确定 未知参数可能的取值范围，使得能以较高的 可信度 保证该范围包含了未知参数的真值.
  
  • 例如：正常人的血糖范围、某地区人的寿命区间、大学生的月消费额度、... ...

---

置信区间

设 $X_1,X_2,...,X_n$ 是来自某个总体的样本，分布函数为 $F(x;\theta)$，其中 $\theta$ 未知.

给定 $\alpha\in(0,1)$，若存在统计量 $\overline{\theta}$ 和 $\underline{\theta}$, 使得

$$\bbox[yellow]{P\left\{\underline{\theta}<\theta<\overline{\theta}\right\}\geq 1-\alpha,}$$

则称区间 $\left(\underline{\theta},\overline{\theta}\right)$ 为参数 $\theta$ 的一个 $1-\alpha$ (双侧)置信区间 (confident interval，缩写 CI)，$\overline{\theta},\underline{\theta}$ 分别称为 $\theta$ 的 双侧置信上、下限. $1-\alpha$ 称为该区间的置信度.

---

单侧置信区间

给定 $\alpha\in(0,1)$, 若存在统计量 $\overline{\theta}$, 使得

$$\bbox[yellow]{P\left\{\theta<\overline{\theta}\right\}\geq 1-\alpha,}$$

则称区间 $\left(-\infty,\overline{\theta}\right)$ 为参数 $\theta$ 的一个 $1-\alpha$ 单侧置信区间，$\overline{\theta}$ 称为 $\theta$ 的 单侧置信上限.

• 同理可以定义 $\theta$ 的单侧置信下限.

---

例：理想的键盘高度

• 为了设计出一款工作效率和舒适度最理想的键盘，设计师将关注的重点放在了键盘托架的高度上.
• 为了得到最理想的高度范围，设计师邀请了 31 位熟练的打字员，分别获取了对他们来说最为理想的托架高度.
• 结果得到的平均值为 $\overline{x}=80.0$ cm. 假设打字员所钟意的托架高度服从方差为 4 均值为 $\mu$ 的正态分布.
• 试给出 $\mu$ 的一个 $0.95$ 置信区间.

---

分析：

• 设 $X_1,X_2,...,X_n$ 为来自总体 $N(\mu,\sigma^2)$ 的样本.
• 于是 $\overline{X}\sim N\left(\mu,\displaystyle \frac{\sigma^2}{n}\right)$, 进而 $Z=\displaystyle \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1)$.
• 注意到 $P\left\{u_{\alpha/2}<\displaystyle \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}< u_{1-\alpha/2}\right\}=1-\alpha$.
• 即 $P\left\{\displaystyle \overline{X}+u_{\alpha/2}\frac{\sigma}{\sqrt{n}}<\mu<\overline{X}+u_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\right\}=1-\alpha$.
• 代入本例中的数值计算，可得 $(79.3,80.7)$ 是 $\mu$ 的一个 $0.95$ 置信区间.

---

置信区间的含义

上面的例子中，

• 因为 $\mu$ 是一个常数（但取值未知），以上求得的置信区间的意义并不能理解为 $P\{\mu\in(79.3,80.7)\}=0.95$.
• 而只能理解为 $P\left\{\mu\in(\overline{X}-0.7,\overline{X}+0.7)\right\}=0.95$，
• 即该随机区间中包含 $\mu$ 的概率为 $0.95$.

---

置信区间不具有唯一性

前例中，$\mu$ 的 $1-\alpha$ 置信区间为

$$\left(\overline{x}+u_{\alpha/2}\frac{\sigma}{\sqrt{n}},\overline{x}+u_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\right)$$

• 为了方便，可以简写为 $\displaystyle \bbox[yellow]{\overline{x}\mp u_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}.}$
• 显然，置信区间并不具有唯一性，也不一定要求两侧具有对称性.
• 事实上，对于本例而言，对任何一个 $\beta\in[0,\alpha]$，$\displaystyle \left(\overline{x}+u_{\beta}\frac{\sigma}{\sqrt{n}},\overline{x}+u_{1-\alpha-\beta}\frac{\sigma}{\sqrt{n}}\right)$ 都是满足要求的置信区间.

---

例：双侧置信区间的宽度

• 某计算机系统上特定的编辑指令的响应时间服从标准差为 25 毫秒的正态分布.
• 安装新的操作系统后，希望对其平均响应时间的均值 $\mu$ 重新进行估计.
• 假设安装新的操作系统后，响应时间仍服从正态分布，且标准差不变.
• 为了使得 $\mu$ 的 $0.95$ 置信区间宽度不超过 10，样本的容量至少要有多大？

---

分析： 参考前例，置信区间为 $\left(\overline{x}-u_{0.975}\frac{\sigma}{\sqrt{n}},\overline{x}+u_{0.975}\frac{\sigma}{\sqrt{n}}\right)$，依题意须满足

$$2(u_{0.975})\frac{\sigma}{\sqrt{n}}\leq 10,$$

即 $\displaystyle \sqrt{n}\geq 2(1.96)\frac{25}{10}=9.8$，故 $n\geq (9.8)^2=96.04$.

• 注: 在样本容量不变的前提下，如果提高置信水平，置信区间的宽度将会增加. 此时，可以说：估计的可靠性 (reliability) 提高了，但估计的精确度 (precision) 有所下降.

---

Jerzy Neyman (1894-1981)

• 现今的区间估计理论是由原籍波兰的美国统计学家 Jerzy Neyman 于 20 世纪 30 年代建立起来的.
• Neyman 被称为”来自生活的统计学家“，毕生热心于且精通于应用的，后半生的工作更是遍历了生物学、宇宙学、气象学等等诸多领域.
• 求区间估计一般方法：依据波动理论的 枢轴变量法.

---

枢轴变量

设 $X_1,X_2,...,X_n$ 为对未知参数 $\theta$ 进行区间估计所需的样本. 所谓枢轴变量 (pivotal quantity) $T$，是指：

1. $T$ 是 $X_1,X_2,...,X_n$ 和 $\theta$ 的函数.
   
   • $T$ 不是统计量.

2. $T$ 的分布与 $\theta$ 或其他的任何未知参数均无关.

   • 无论 $\theta$ 如何取值，$T$ 的分布不变.

   • 利用枢轴变量推导参数置信区间的方法称为枢轴变量法.

---

用枢轴变量法求置信区间

1. 构造样本的函数 $g\left(X_{1},\cdots, X_{n} ; \theta\right)$，也即 枢轴变量 (Pivotal Quantity).
2. 对置信度 $1-\alpha$，确定 $g\left(X_{1}, \cdots, X_{n} ; \theta\right)$ 的分布的两个分位点 $\eta_{\alpha/2}$ 和 $\eta_{1-\alpha/2}$, 使得 $\bbox[yellow]{P\left\{\eta_{\alpha / 2}< g< \eta_{1-\alpha / 2}\right\}=1-\alpha.}$
   
   • 注： 在没有事先声明的情况下，默认地按以上方式取两侧的分位点，所得到的的置信区间称为 等尾置信区间.
3. 解不等式 $\eta_{\alpha / 2}< g\left(X_{1}, \cdots, X_{n} ; \theta\right)< \eta_{1-\alpha / 2}$, 得到置信区间：$\left(\underline{\theta}, \overline{\theta}\right)$.

---

例：理想的键盘高度

已知 $\overline{x}=80.0$, 理想高度服从 $\sigma=2.0$ 的正态分布，求 $\mu$ 的 $0.95$ 置信区间.

• 枢轴变量：$Z=\displaystyle \frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1)$.
• 思考: 如果本例中 $\sigma$ 也是未知的，以上的 $Z$ 还是枢轴变量吗？
  
  1. 如果不是，应该如何定义枢轴变量？
  2. 枢轴变量的选择是唯一的吗？

---

单个正态总体的区间估计

已知 $X_1,X_2,...,X_n$ 为来自正态总体 $N(\mu,\sigma^2)$ 的样本, 分别考虑如下四个区间估计问题:

1. $\sigma^2$ 已知，求 $\mu$ 的置信区间.
2. $\sigma^2$ 未知，求 $\mu$ 的置信区间.
3. $\mu$ 已知，求 $\sigma^2$ 的置信区间.
4. $\mu$ 未知，求 $\sigma^2$ 的置信区间.

---

单正态总体的 1-α 置信区间

$$\boxed{ \begin{array}{c|c|c|c|c|c} \text{待估参数} & \text{条件} & \text{枢轴变量} & \text{分布} & \text{双侧置信区间下、上限} & \text{单侧置信下、上限}\\[1em] \hline \mu & \sigma^2\text{已知} & \frac{\overline{X}-\mu}{\sigma/\sqrt{n}} & N(0,1) & \overline{x}\mp u_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} & \overline{x}\mp u_{1-\alpha}\frac{\sigma}{\sqrt{n}}\\[1em] \hline \mu & \sigma^2\text{未知} & \frac{\overline{X}-\mu}{\tilde{S}/\sqrt{n}} & t(n-1) & \overline{x}\mp t_{1-\alpha/2}(n-1)\frac{\tilde{s}}{\sqrt{n}} & \overline{x}\mp t_{1-\alpha}(n-1)\frac{\tilde{s}}{\sqrt{n}}\\[1em] \hline \sigma^2 & \mu\text{已知} & \sum\limits_{i=1}^n\left(\frac{X_i-\mu}{\sigma}\right)^2 & \chi^2(n) & \frac{\sum\limits_{i=1}^n(x_i-\mu)^2}{\chi^2_{1-\alpha/2}(n)},\; \frac{\sum\limits_{i=1}^n(x_i-\mu)^2}{\chi^2_{\alpha/2}(n)} & \frac{\sum\limits_{i=1}^n(x_i-\mu)^2}{\chi^2_{1-\alpha}(n)},\; \frac{\sum\limits_{i=1}^n(x_i-\mu)^2}{\chi^2_{\alpha}(n)}\\[1em] \hline \sigma^2 & \mu\text{未知} & \sum\limits_{i=1}^n\left(\frac{X_i-\overline{X}}{\sigma}\right)^2 & \chi^2(n-1) & \frac{\sum\limits_{i=1}^n(x_i-\overline{x})^2}{\chi^2_{1-\alpha/2}(n-1)},\; \frac{\sum\limits_{i=1}^n(x_i-\overline{x})^2}{\chi^2_{\alpha/2}(n-1)} & \frac{\sum\limits_{i=1}^n(x_i-\overline{x})^2}{\chi^2_{1-\alpha}(n-1)},\; \frac{\sum\limits_{i=1}^n(x_i-\overline{x})^2}{\chi^2_{\alpha}(n-1)} \end{array} }$$

---

提示： 求 $\sigma^2$ 的 $1-\alpha$ 置信区间（假设 $\mu$ 已知）

1. 求双侧置信区间

• 枢轴变量 $\chi^2=\sum\limits_{i=1}^n\left(\frac{X_i-\mu}{\sigma}\right)^2\sim\chi^2(n)$.
• 设 $P\left\{C_1\leq\sigma^2\leq C_2\right\}=1-\alpha$，也即
  
  • $P\left\{\frac{1}{C_2}\sum\limits_{i=1}^n(X_i-\mu)^2\leq\frac{1}{\sigma^2}\sum\limits_{i=1}^n(X_i-\mu)^2\leq \frac{1}{C_1}\sum\limits_{i=1}^n(X_i-\mu)^2\right\}=1-\alpha$.
• 取 $\frac{1}{C_2}\sum\limits_{i=1}^n(X_i-\mu)^2=\chi^2_{\alpha/2}(n)$，$\frac{1}{C_1}\sum\limits_{i=1}^n(X_i-\mu)^2=\chi^2_{1-\alpha/2}(n)$.
• 解得 $C_1=\frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{1-\alpha/2}(n)}$，$C_2=\frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{\alpha/2}(n)}$.

---

2. 求单侧置信下限

• 枢轴变量 $\chi^2=\sum\limits_{i=1}^n\left(\frac{X_i-\mu}{\sigma}\right)^2\sim\chi^2(n)$.
• 设 $P\left\{C_1\leq\sigma^2\right\}=1-\alpha$，也即
  
  • $P\left\{\frac{1}{\sigma^2}\sum\limits_{i=1}^n(X_i-\mu)^2\leq \frac{1}{C_1}\sum\limits_{i=1}^n(X_i-\mu)^2\right\}=1-\alpha$.
• 取 $\frac{1}{C_1}\sum\limits_{i=1}^n(X_i-\mu)^2=\chi^2_{1-\alpha}(n)$，解得 $C_1=\frac{\sum\limits_{i=1}^n(X_i-\mu)^2}{\chi^2_{1-\alpha}(n)}$.

---

例：飞机的飞行高度

为了提高可靠性和测量精度，飞机通常安装了若干个高度仪. 设飞机实际飞行高度为 $\mu$ 时每个高度仪时测量值 $X\sim N(\mu,64)$，而飞机仪表上显示的飞行高度是所有的高度测量值的平均值. 在置信水平 $1-\alpha=0.98$ 下，求解下列问题：

1. 若要保证飞行仪表上显示的飞信高度的绝对误差不超过 $12$ m，问飞机上至少安装多少个高度仪？
2. 若飞机装有 $4$ 个高度仪，飞行仪表上显示的飞行高度是 $9813$ m，问飞机实际飞行在什么高度范围？

---

提示：

• 1. 假设有 $n$ 个高度仪，高度测量值分别为 $X_1,X_2,...,X_n$，则 $\overline{X}\sim N\left(\mu,\frac{64}{n}\right)$.
• 问题等价于，要使 $P\left\{|\overline{X}-\mu|\leq 12\right\}\geq 0.98$，$n$ 至少需要取多大？
• 上式也即 $P\left\{\frac{-12}{8/\sqrt{n}}<\frac{\overline{X}-\mu}{8/\sqrt{n}}<\frac{12}{8/\sqrt{n}}\right\}\geq 0.98$.
• 由此可得 $\frac{12}{8/\sqrt{n}}>u_{1-\frac{\alpha}{2}}=u_{0.99}$，即 $n>64\cdot\frac{u_{0.99}^2}{144}\approx 2.41$.
• 结论：安装至少 $3$ 个高度仪就可以满足要求.

---

• 1. 此时 $\overline{X}\sim N(\mu,16)$，进而 $\frac{\overline{X}-\mu}{4}\sim N(0,1)$.
• 置信区间为 $u_{0.01}<\frac{\overline{X}-\mu}{4}<u_{0.99}$.
• 或 $\mu\in(\overline{x}-u_{0.99}\cdot 4,\overline{x}-u_{0.99}\cdot 4)\approx(\overline{x}-9.32,\overline{x}+9.32).$
• 已知 $\overline{x}=9813$，故此时飞机的实际高度范围为 $(9803.68,9822.32)$.

---

例：灯泡的寿命

从灯泡厂随机抽取 $10$ 只灯泡，进行寿命试验，测得数据如下（单位：小时）

$1050,1100,1080,1120,1200,1250,1040,1130,1300,1200.$

设灯泡寿命服从正态分布，给出这批灯泡的平均寿命及方差的置信度为 $95\%$ 的置信区间.

---

解：

• 设 $X$ 为灯泡的寿命，设 $X\sim N(\mu,\sigma^2)$，其中 $\mu,\sigma^2$ 均未知.
• $\mu$ 的置信度为 $1-\alpha$ 置信区间是 $\left(\bar{x} \mp t_{1-\alpha / 2}(n-1) \frac{\tilde{s}}{\sqrt{n-1}}\right)$.
• 利用抽样数据进行计算，$\overline{x}=\frac{1}{10}(1050+\cdots+1200)=1147$.
  
  • $\tilde{s}=\sqrt{\frac{1}{9} \sum_{i=1}^{10}\left(x_{i}-\bar{x}\right)^{2}}=\sqrt{\frac{1}{9} \sum_{i=1}^{10}\left(x_{i}-1147\right)^{2}}=82.59$.
• 查表 $t_{1-\alpha / 2}(n-1)=t_{0.975}(9)=2.26$，故 $\mu$ 的置信度为 $95\%$ 的置信区间为 $\left(1147 \mp 2.26 \times \frac{82.59}{\sqrt{9}}\right)=(1084.78,1209.22)$.

---

• $\sigma^2$ 的置信度为 $1-\alpha$ 的置信区间为 $\left(\frac{(n-1) \tilde{s}^{2}}{\chi_{1-\alpha / 2}^{2}(n-1)}, \frac{(n-1) \tilde{s}^{2}}{\chi_{\alpha / 2}^{2}(n-1)}\right)$.
• $\tilde{s}^{2}=82.59^{2}=6821.10$.
• $\chi_{\alpha / 2}^{2}(n-1)=\chi_{0.025}^{2}(9)=2.7$.
• $\chi_{1-\alpha / 2}^{2}(n-1)=\chi_{0.975}^{2}(9)=19.023$.
• $\sigma^2$ 的置信度为 $95\%$ 的置信区间为 $\left(\frac{10 \times 6821.10}{19.023}, \frac{10 \times 6821.10}{2.7}\right)=(3585.71,25263.33).$

---

双正态总体的区间估计

• 设 $X_1,X_2,...,X_m$ 和 $Y_1,Y_2,\ldots,Y_n$ 分别为来自 $N(\mu_1,\sigma_1^2)$ 和 $N(\mu_2,\sigma_2^2)$ 的样本，且二者相互独立.
• 试对其均值的差 $\mu_1-\mu_2$ 和方差的比值 $\displaystyle \frac{\sigma_1^2}{\sigma_2^2}$ 给出区间估计.

---

双正态总体的 1-α 置信区间

$$\boxed{ \begin{array}{c|c|c|c|c} \text{待估参数} & \text{条件} & \text{枢轴变量及其分布} & \text{双侧置信区间下、上限} & \text{单侧置信下、上限}\\[1em] \hline \mu_1-\mu_2 & \sigma_1^2,\sigma_2^2\text{已知} & \frac{\displaystyle \overline{X}-\overline{Y}-(\mu_1-\mu_2)}{\sqrt{\displaystyle \frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}}} \sim N(0,1) & (\overline{x}-\overline{y})\mp u_{1-\alpha/2}\sqrt{\displaystyle \frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}} & (\overline{x}-\overline{y})\mp u_{1-\alpha}\sqrt{\displaystyle \frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}}\\[1em] \hline \mu_1-\mu_2 & \sigma_1^2=\sigma_2^2=\sigma^2\text{未知} & \displaystyle \frac{\displaystyle \overline{X}-\overline{Y}-(\mu_1-\mu_2)}{S_{\omega}\sqrt{\displaystyle \frac{1}{m}+\frac{1}{n}}} \sim t(m+n-2) & \displaystyle \overline{x}-\overline{y}\mp t_{1-\alpha/2}(m+n-2){s_{\omega}\sqrt{\displaystyle \frac{1}{m}+\frac{1}{n}}} & \displaystyle \overline{x}-\overline{y}\mp t_{1-\alpha}(m+n-2){s_{\omega}\sqrt{\displaystyle \frac{1}{m}+\frac{1}{n}}}\\[1em] \hline \sigma_1^2/\sigma_2^2 & \mu_1,\mu_2\text{已知} & \frac{\displaystyle \frac{1}{m}\sum\limits_{i=1}^m\left(\frac{X_i-\mu_1}{\sigma_1}\right)^2}{\displaystyle \frac{1}{n}\sum\limits_{i=1}^n\left(\frac{Y_i-\mu_2}{\sigma_2}\right)^2} \sim F(m,n) & \begin{array}{c}\frac{n\sum\limits_{i=1}^m(x_i-\mu_1)^2}{m\sum\limits_{i=1}^n(y_i-\mu_2)^2}\frac{1}{F_{1-\alpha/2}(m,n)}\\ \frac{n\sum\limits_{i=1}^m(x_i-\mu_1)^2}{m\sum\limits_{i=1}^n(y_i-\mu_2)^2}\frac{1}{F_{\alpha/2}(m,n)}\end{array} & \begin{array}{c}\frac{n\sum\limits_{i=1}^m(x_i-\mu_1)^2}{m\sum\limits_{i=1}^n(y_i-\mu_2)^2}\frac{1}{F_{1-\alpha}(m,n)}\\ \frac{n\sum\limits_{i=1}^m(x_i-\mu_1)^2}{m\sum\limits_{i=1}^n(y_i-\mu_2)^2}\frac{1}{F_{\alpha}(m,n)}\end{array} \\[1em] \hline \sigma_1^2/\sigma_2^2 & \mu_1,\mu_2\text{未知} & \displaystyle \frac{\tilde{S}_1^2/\sigma_1^2}{\tilde{S}_2^2/\sigma_2^2} \sim F(m-1,n-1) & \begin{array}{c}\frac{\tilde{s}_1^2}{\tilde{s}_2^2}\frac{1}{F_{1-\alpha/2}(m-1,n-1)}\\ \frac{\tilde{s}_1^2}{\tilde{s}_2^2}\frac{1}{F_{1-\alpha/2}(m-1,n-1)}\end{array} & \begin{array}{c}\frac{\tilde{s}_1^2}{\tilde{s}_2^2}\frac{1}{F_{\alpha}(m-1,n-1)}\\ \frac{\tilde{s}_1^2}{\tilde{s}_2^2}\frac{1}{F_{\alpha}(m-1,n-1)}\end{array} \end{array} }$$

---

例：比较子弹的初速度

• 随机地取 I 型子弹 $10$ 发, 得到枪口速度的平均值为 $\overline{x}_1=500$(m/s), 修正的标准差 $\tilde{s}_1=1.10$(m/s).
• 随机地取 II 型子弹 $20$ 发, 得到枪口速度的平均值为 $\overline{x}_2=496$(m/s), 修正的标准差 $\tilde{s}_2=1.20$(m/s).
• 假设两总体都可认为近似地服从正态分布, 且由生产过程可认为它们的方差相等.
• 求两总体均值差 $\mu_1-\mu_2$ 的置信度为 $0.95$ 的置信区间.

---

解：

• 由实际情况，可认为分别来自两个总体的样本是相互独立的.
• 由于它们的方差相等且未知，故 $\mu_1-\mu_2$ 的置信度 $1-\alpha$ 的置信区间为 $\left((\overline{x}-\overline{y}) \pm t_{1-\alpha / 2}(m+n-2) s_{\omega} \sqrt{\frac{1}{m}+\frac{1}{n}}\right)$.
• 其中 $1-\alpha=0.95$, $t_{0.975}(28)=2.0484$, $s_{\omega}=\sqrt{\frac{9 \times 1.10^{2}+19 \times 1.20^{2}}{28}}=1.1688$.
• 故两总体均值差 $\mu_1-\mu_2$ 的置信度为 $0.95$ 的置信区间为 $(4 \pm 0.93)=(3.07,4.93)$.

---

小结

1. 点估计
   
   • 矩估计与最大似然估计
   • 点估计的评估准则
     
     • 无偏性、有效性、相合性
2. 区间估计
   
   • 枢轴变量法
   • 单正态和双正态总体的区间估计
   • 单侧置信区间