@zzzc18
2017-05-10T12:18:01.000000Z
字数 1301
阅读 1795
bzoj 1002(递推关系)
bzoj
Description
轮状病毒有很多变种,所有轮状病毒的变种都是从一个轮状基产生的。一个N轮状基由圆环上N个不同的基原子和圆心处一个核原子构成的,2个原子之间的边表示这2个原子之间的信息通道。如下图所示

N轮状病毒的产生规律是在一个N轮状基中删去若干条边,使得各原子之间有唯一的信息通道,例如共有16个不同的3轮状病毒,如下图所示

现给定n(N<=100),编程计算有多少个不同的n轮状病毒
Input
第一行有1个正整数n
Output
计算出的不同的n轮状病毒数输出
Sample Input
3
Sample Output
16
solve
我们只要选择连在一起有几个就行了,相当于把n分成很多段连续的圆弧
可以由递推关系来解决
以下面n=4为例
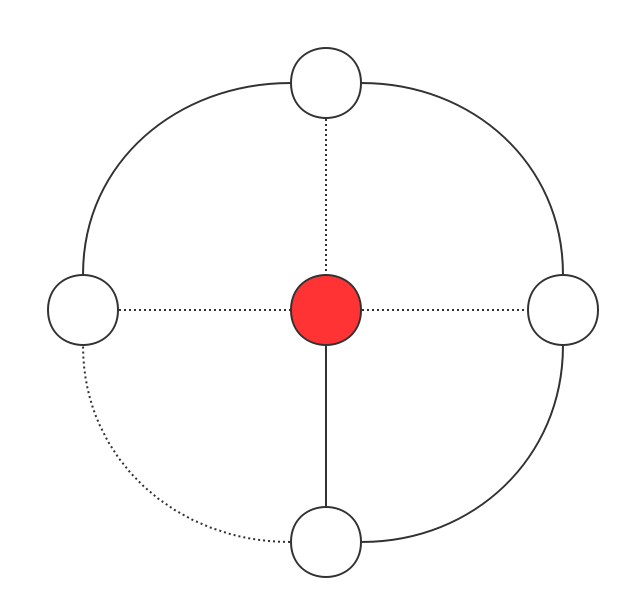
上图为一种可行解,弧上的实、虚线可互相替换,十字上的实、虚线可互相替换
有4*4种方法
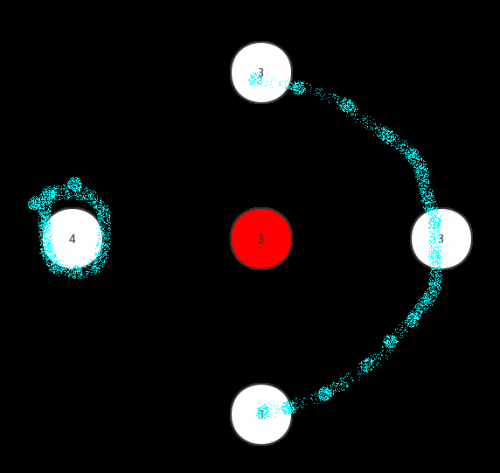
上图,弧上n=3的点集再连上4的,有1*f(3)种的情况
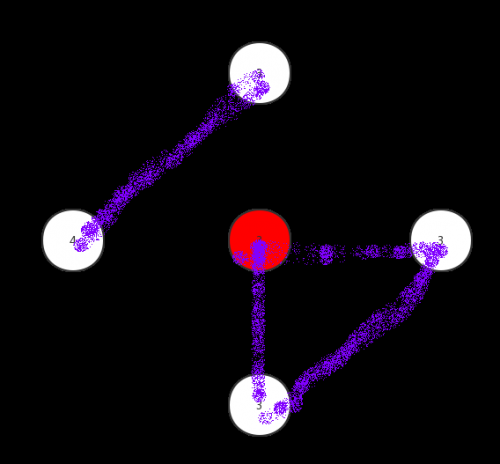
上图,相连的是同一点集,显然有2*f(2)种
同理,还有3*f(1)种
于是,有了f(4)=4*4+1*f(3)+2*f(2)+3*f(1)
同样的
f(i)=i*i+1*f(i-1)+2*f(i-2)+3*f(i-3)+...+(n-1)*f(1)
这时再将上式改为递推式
f(i)=2*i-1 + f(1) + f(2) + ... + f(i-1) + f(i-1)
怎么来的呢?
还以n=4为例
| 当前式 | 常数 | f(1) | f(2) | f(3) |
|---|---|---|---|---|
| f(1) | 1*2-1 | 0 | 0 | 0 |
| f(2) | 2*2-1 | 1 | 0 | 0 |
| f(3) | 3*2-1 | 1 | 1 | 0 |
| f(4) | 4*2-1 | 1 | 1 | 1 |
| ANS(4)(求和) | 4^2 | 3 | 2 | 1 |
然后就可以搞事情了,递推式推到底就AC了
注意高精
#include<cstdio>#include<cstring>#include<iostream>#define MAXN 1000using namespace std;int n;struct BIGNUM{int num[MAXN];int len;BIGNUM(){memset(num,0,sizeof(num));len=1;}}SUM,f,ANS;BIGNUM ADD(const BIGNUM &x,const BIGNUM &y){int len=max(x.len,y.len);int i;BIGNUM tmp;for(i=0;i<=len;i++){tmp.num[i]+=x.num[i]+y.num[i];tmp.num[i+1]=tmp.num[i]/10;tmp.num[i]%=10;}if(tmp.num[len])len++;tmp.len=len;return tmp;}void PRINT(const BIGNUM & x){int i;for(i=x.len-1;i>=0;i--)printf("%d",x.num[i]);}void solve(){int i;for(i=1;i<=n;i++){f.num[0]+=i*2-1;f=ADD(f,SUM);SUM=ADD(f,SUM);ANS=f;}}int main(){scanf("%d",&n);solve();PRINT(ANS);return 0;}
