玩命的数据分析学习日志（三） - 神经网络探讨1

devilogic

点融网沙龙 - 神经网络权值直接确定法的探讨

---

这是一个人人都在谈大数据的时代，貌似你不谈就显的格外Low...

神经网络ABC

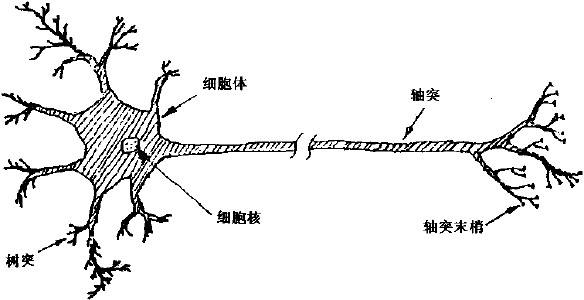
单个神经元

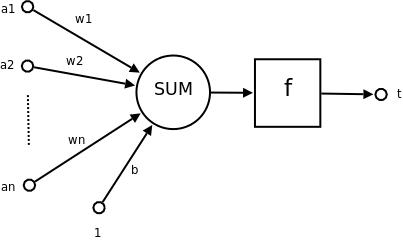
前向反馈网

真实的目标与网络的作用

真实的目标是一个未知的函数$f(X)$，而这个函数多数情况下也是没有正解的。在最一般的情况下，神经网络是要逼近一个最小二乘解。
那就是说用模型的最小二乘解来逼近目标$f(x)$的最小二乘解。
确切的解与逼近都是特殊情况。

三体

这是一个控制维度的游戏，在神秘的世界中找寻到那个维度

1. 输入 -> 特征 -> 输入变量 -> 观察到的特征
2. 神经元 -> 权重 -> 方程的个数 -> 特征对输出的贡献
3. 输出 -> 解值 -> 解方程组方程的个数 -> 预测值
4. 隐藏层数 -> 尝试不同线性空间 -> 方程组的个数 -> 尝试找寻那个神秘的变量或者剔除提纯特征集

一般而言 $方程的数量(特征) \lt 变量的数量(分类,拟合的值)$ 是一个超定方程组，只能求最小二乘解。

让我们先来探讨一下决策树

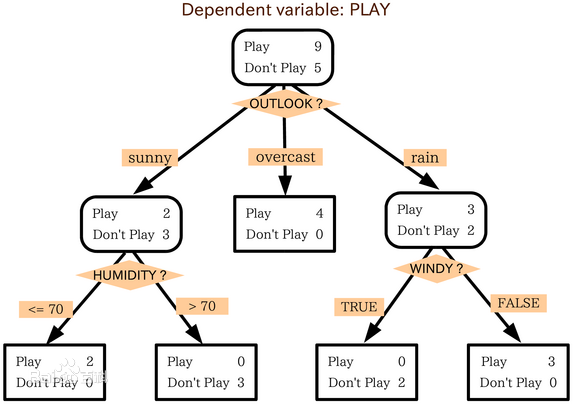
一个熵计算的过程$entropy = log_2^{P_1} + log_2^{P_2} + \cdots+ log_2^{P_n}$。按照熵的最小化程度来进行分类。
让我们替换一下上面的公式为：

$$P(C_x | P_1,P_2,\ldots,P_n) = log_2^{entropy} = P_1 \times P_2 \times \cdots \times P_n$$
这是按照$x$来划分样本空间导致结果为$C$的后验概率，可以把这棵树转换成一个方程组。目前我还没找到相关论文，不过应该是可以的(这个问题让不做CTO的人来研究吧)。那么一般这就是超定方程组(方程数量多于变量的个数)。其实就是一个无隐层的神经网络（输入 -> 输出）。
而一个决策树是否可以训练成功完全依赖一个样本集的特征。那么最重要的一点就是这个特征集合是否可以覆盖假设空间。那么不满足这个条件，那么训练的将失败。如果特征缺失掉的化，如何找寻到这个特征就很重要了。这就不是决策树可以解决的问题了。
而这个特征集合尺寸其实就是模型世界的维度。那么这个模型是否能逼近真实目标呢？
想想支持向量机(SVM)算法，它的做法是升维，形成高维打低维的情况。$x_3^{'} = f(x_1,x_2)$。其中这个$x_3^{'}$是通过$x_1,x_2$通过某个函数进行近似。原理是在这冥冥之中有一个神秘的变量与现实观察到特征存在某种神秘的联系。

降维打击算式对特征的提纯吧～～～

再回来想想神经网络这种东西吧，本来已经证明了三层BP网络具有任意的非线性逼近能力了。为什么还要那么多层呢？而层数的确定以及激励函数的为什么又那么不确定呢？

控制层数与选择激励函数可以看成是对找寻神秘特征与削减不必要特征的一次次尝试。

学习的过程

这是一个在$k$轮迭代过程中调解权值矩阵的过程，通过这个过程最终来逼近到目标函数$f(x)$。

一个找解的过程 - 梯度下降法(gradient descent)

1.导数为正则说明比正解大
2.导数为负则说明比正解小

根据以上我们需要按照导数的反方向来调节。

让我们来看下根据梯度下降法的完整学习过程。这里首先说明一些条件。

• $x_{ji}$ 单元$j$的第$i$个输入
• $w_{ji}$ 与单元$j$的第$i$个输入相关联的权值
• $net_j = \sum_iw_{ji}x_{ji}$ 单元$j$的输入的加权和
• $o_j$ 单元$j$计算出的输出
• $t_j$ 单元$j$的目标输出
• $\sigma$ sigmoid函数
• outputs 网络最后一层的单元的集合
• Downstream{j} 单元的直接输入中包含单元$j$的输出的单元的集合

这里的$\sigma$函数可以替换成任何传输函数$f(x)$

误差

通过公式来计算出网络最终的输出与目标的误差
$E_d(\overrightarrow{w}) \equiv \frac{1}{2}\sum_{k \in outputs}(t_k - o_k)^2$

其实也可以其他误差函数，但是均方差是可微函数。

我们对这个误差进行链式求导来得到梯度。

$$\begin{align} \frac{\Delta E_d}{\Delta w_{ji}} & = \frac{\Delta E_d}{\Delta net_j}\frac{\Delta net_j}{\Delta w_{ji}} \\ &= \frac{\Delta E_d}{\Delta net_j}x_{ji} \end{align}$$

那么我们主要是对$\frac{\Delta E_d}{\Delta net_j}$来进行计算，其中的$net_j$ 可以替换成任意要修订层的情况。

情况1:输出单元的权值训练法则

$$\frac{\Delta E_d}{\Delta net_j} = \frac{\Delta E_d}{\Delta o_j}\frac{\Delta o_j}{\Delta net_j}$$
首先考虑公式的第一项
$$\frac{\Delta E_d}{\Delta o_j} = \frac{\Delta}{\Delta o_j}\frac{1}{2}\sum_{k \in outputs}(t_k - o_k)^2$$
除了当$k=j$时，所有输出单元$k$的导数$\frac{\Delta}{\Delta o_j}(t_k - o_k)^2$为$0$。所以我们不必对多个输出单元求和，只需要设$k=j$。
$$\begin{align}\frac{\Delta E_d}{\Delta o_j} = -(t_j - o_j)\end{align}$$
现在考虑第二项，既然$o_j = \sigma(net_j)$，如果选用sigmod函数的化其导数为$\sigma(net_j)(1-\sigma(net_j))$。所以我们得到:
$$\frac{\Delta E_d}{\Delta net_j} = -(t_j - o_j)o_j(1-o_j) = -\delta_j$$
则
$$\Delta w_{ji} = -\eta \frac{\Delta E_d}{\Delta w_{ji}} = \eta(t_j - o_j)o_j(1 - o_j)x_{ji}$$

情况2:隐藏单元的权值训练法则

我们再来看下任意隐藏单元的情况，$w_{ji}$必须考虑$w_{ji}$间接的影响网络输出，从而影响$E_d$。

$$\begin{align}\frac{\Delta E_d}{\Delta net_j} &= \sum_{k \in Downstream(j)}\frac{\Delta E_d}{\Delta net_k}\frac{\Delta net_k}{\Delta net_j} \\ &= \sum_{k \in Downstream(j)}-\delta_k \frac{\Delta net_k}{\Delta net_j} \\ &= \sum_{k \in Downstream(j)} -\delta_k\frac{\Delta net_k}{\Delta o_j}\frac{\Delta o_j}{\Delta net_j} \\ &= \sum_{k \in Downstream(j)}-\delta_kw_{kj}\frac{\Delta o_j}{\Delta net_j} \\ &= \sum_{k \in Downstream(j)}-\delta_kw_{kj}o_j(1-o_j)\end{align}$$

上式中$net_k = w_{kj}o_j + w_{ki}o_j + \cdots + w_{kn}o_n$
重新组织各项并使用$\delta_j$表示$-\frac{\Delta E_d}{\Delta net_j}$，我们得到：

$$\delta_j = o_j(1-o_j)\sum_{Downstream(j)}\delta_kw_{kj}$$
则
$$\Delta w_{ji} = \eta o_j(1-o_j)\sum_{Downstream(j)}\delta_kw_{kj}x_{ji}$$

泛化上述公式

$o_j(1-o_j)$是sigmod的导数，那么如果我们将这个替换成任意激励函数的导函数则有:

$$\Delta w_{ji}^m = \eta f^{'}_j \sum_{Downstream(j)} w_{ji}^m f^{'}_k x_{kj}^m$$
上述中的$m$表示第$m$次迭代。

总结

1. 计算输出层的误差并生成梯度
2. 使用梯度对每个隐藏层的每个神经元进行求导并调节

再回头来看看$E$

在上述调节过程中，首先是梯度的产生在整个学习过程中起到关键作用。所以我们先来看看$E$的产生。

$$E=\frac{1}{2}\sum_{i=1}^m(t_i - \sigma(\sum_{j=1}^{n}w_{ij}x_{ij})))^2$$
其中在这里的$x_{ij}$表示不同的输入，这里我们让上述公式变的简单一些仅有一个输入$x$时的情况并且使用线性函数作为激励函数,并将$t$变成$y$,那么：
$$E=\frac{1}{2}\sum_{i=1}^m(y_i - w_ix_i))^2$$
这样就清爽多了。

这里的$y_i$其实就是真实的目标值，那么按照我们文章所说这其实是目标函数$\Phi(x)$的一个最小二乘解(一般状况下)。而这里的$w_ix_i$是我们对$\Phi(x)$解的一个逼近。那么单使用权和逼近有点弱暴了。接下来我们使用幂函数作为一个特殊情况来逼近目标函数则

$$\Phi(x)$ \approx \phi(w_0x^0 + w_1x^1 + \cdots + w_nx^p)$$
那么
$$\begin{align}E &=\frac{1}{2}\sum_{i=1}^m(\Phi(x) - \phi(w_0x^0 + w_1x^1 + \cdots + w_nx^p)))^2 \\ &= \frac{1}{2}\sum_{i=1}^m(\Phi(x) - \sum_{p=0}^{n-1}w_p\phi(x^p))^2\end{align}$$
其中的$\phi(\cdot)$可以使用任意线性无关的正交多项式来代替。我们对上式的第$j$个权进行求导，则得到$\frac{\Delta E}{\Delta w_j}$这个梯度。
再次回头看看权值的更新法则
$$w_j(k+1) = w_j(k) - \eta \frac{\Delta E}{\Delta w_j}$$

当$k$无限大时

当$k$无限大，就是说训练已经收敛时，那么最良好的情况是$w_j(k+1) = w_j(k)$，则说明了梯度为$0$，那么：

$$\eta \frac{\Delta E}{\Delta w_j} = 0$$
那么可以得出下式：
$$\frac{\Delta E}{\Delta w_j} = X^T(Xw - \gamma)$$
其中
$$X = \begin{bmatrix}\phi_0(x_1) & \phi_1(x_1) & \cdots & \phi_{n-1}(x_1) \\ \phi_0(x_2) & \phi_1(x_2) & \cdots & \phi_{n-1}(x_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_0(x_m) & \phi_1(x_m) & \cdots & \phi_{n-1}(x_m) \end{bmatrix}$$
这里只是将$E$中的$\sum\sum$展开而已。
这里通过线性代数中求矩阵伪逆的算法来的到系数$w$的最小二乘解。
$$\omega : = lim_{k \rightarrow \inf}w(k) = (X^TX)^{-1}X^T\gamma$$

推荐书籍

感谢与抱歉

首先感谢点融网给了这次做技术交流的平台，由于时间原因，一个会写代码的CTO并不能完整的探讨此类话题，这份演讲稿显得仓促之急，没有对此中技术的充分讨论以及应用。希望下次还有这样的机会和大家分享。