@devilogic
2017-12-31T11:37:56.000000Z
字数 19285
阅读 1666
玩命的销售日志 2017.12.31
日志

前段时间刚从大武汉吃热干面回来,连续十几天的出差,感觉人快废掉了。最近嗓子发炎加上天气变冷又感冒了。第一次觉得自己身体抗不住了。话说武汉正宗的热干面刷新了我对热干面的认识,在北京上地某XX鸟饭店吃的就是坨屎。
干了半年销售和售前。唯一的心得体会就是累,是真累,还特消耗时间。除了看小说的时间增多了,其余的时间都少了。原来做技术的时候,感觉做销售有什么啊!不就是每天见见人,聊聊天,出去喝喝酒嘛!有什么啊~~~。干过销售以后,我收回以前所说的屁话。唯一感想就是写程序是闹心,做销售是恶心。
前几天我从小长耍到大的哥们千千说想和我一起跑跑IT类销售,看看是否能帮我在我老家少得可怜的科技企业中推销一些我们的产品。我答应了,就一起跑了趟上海。
话说千千是一个在银行待了10年的老行员了,最初开始给银行推销信用卡,随后又做消费贷、车贷与房贷。据说当初推销信用卡的时候直接推开某些政企单位领导办公室的门,死皮赖脸的要人家全单位办信用卡。貌似他第一辆车就是这样来的。
今年年初从他一个搞设计的朋友那边得到灵感,想在网上卖香薰蜡烛。我当初还以为丫是说笑。一个大老爷们搞这种小资情调的玩意。但是这货从有想法到设计自己的品牌再到建立网店外加建立渠道一共也就两周时间。人们都说一流的行动力比一流的Idea要重要的多。难得的是千千既有行动力又有Idea。从确定走高逼格小众香薰路线到整套的品牌VI设计一周时间,随后自己在家熬香薰,结果工艺不行。被逼无奈丫开始联系代理商一共又花了一周。运营了一个月小店就盈利了。丫又找来我另外一个哥们四强性欲强,性欲强,性欲强,性欲强,重要的事情说四遍两人合伙搞这家小店,四强原本也是安全圈的程序员,搞了几年安全觉得赚钱太少,就去开了一个taobao店卖做蛋糕的模具,做了一年多在成都买了两套房,三辆车(宝马,奥迪,霸道)。当初写程序的时候真没看出他这么会做生意。
注意以下是用水果机在自家餐桌上实拍

重要的是外包装的逼格。

一直闹不懂为啥卖香薰要带个杯子。

不过可能是我太土鳖的缘故,一直理解不了千千所说的生活美学是什么?
总之感觉两人都是人才。找个时间让他两人来娜迦给我们的销售上上课。在他俩身上我总结了一下。
战术方面:
- 脸是什么玩意?
- 一定要包装好看
娜迦就是太把自己这张脸当回事,又太不注意自己的产品形象。山西人和四川人都是图实在的主。娜迦在文档上的功夫非常差。
战略方面:
- 认清自己的客户群体 -
小资情调、生活美学、装逼文艺女青年 - 锁定自己的产品方向 -
主要经营小众品牌香薰,少量周边产品
娜迦有时候什么生意都做,凭着自己技术研究能力强,只要客户有需求就想一套解决方案给客户解决。对自身产品界定不是很明晰,虽然有一个大体的方向,但是仍然不是非常明确。
幸运得是娜迦最好的优点有两个:一是谦虚,二是肯学。向两位淘宝店店主学习取经。
最近出差确实有点多,没时间研究什么技术。也就在飞机与高铁上随便写两行代码练练手。吃饭的手艺不能丢
这里要插播一句,我终于体会到多老板的前几年的心情了,话说多老板当年在成都修了不少房子。赚钱之余还再黑站,和我说手不能生,感觉不写写代码,黑黑站。没有安全感。房地产做不下去了,还能回来做程序员至少还有口饭吃。
在旅途中看小说,写代码之余也思考下我们这个行业。这个行业内的几家企业真是一切跟的风口走。风往哪里刮,牛就往哪里吹。当物联网很火的时候,保护两个电饭锅,空调的APP就叫涉及物联网安全。车联网起风了,那么去给车厂做做APP 保护就叫车联网布局。貌似某家公司还研究过区块链安全。总之哪个行业火,就去给哪个行业做APP加固,就说在涉及这个行业,是为这个行业定制的安全加固方案。其实都很扯蛋。还有些产品也是纯粹概念,反正安全产品对于用户来说,太难进行验证。
梆梆有个产品叫做白盒加密,还为此写了两篇哄小孩子的文章。其实这里想说一下,白盒加密是一个概念,不是一个特定的技术或者算法,更不能用来定义一个产品。这个概念就是指算法与密钥在暴露的情况下,如何保证加密的安全。其实软件保护本身就是白盒加密。不过很少有客户明白。我们就是太缺少这方面的经验,无论是产品概念还是文档形式。
经营企业真的不能有太多技术洁癖
我发现一点是企业对于包装这个事情是给两方面看的,一是老实的客户,二是自以为是的VC。前者是对自己的产品进行包装来骗客户,后者是对自己的公司战略进行包装来骗融资。
想想我们确实应该和千千去学习一下,在网上卖带香味的蜡烛和用玻璃瓶装的火柴,就说自己从事生活美学方面的工作。并且对此深信不疑,为此还专门去了日本,说是要学习体验。
不过对于准备一辈子都要做程序员的人来说还是聊聊技术问题吧!都说有两样东西每个男人都会喜欢,一个是车,一个是枪。我对车没太多的执念,但对于后者如果在法律允许下我可能会在家里搞一个军火库出来。但这几天的研究对象是前者,起因是最近正好在看车,其次是因为车联网这么火,就顺手看一下。反正飞机上也没其他的事情可做。
正好前段时间有朋友给了我篇关于驾驶安全方面的论文,我也从网上搜了一些。想自己闲暇无事实现一套这样的程序。从驾驶风格来给安全性和经济性打个分。所以就有了以下的文章。
问题分析
下面主要阐述了驾驶安全性评估方面的算法。我的想法是这样的,程序的输入是一组一辆车在一段路的驾驶参数,程序对他这段路的驾驶安全性进行打分。以下这套模型是取自一篇清华大学和千方集团的论文。
安全驾驶模型
| 指标类 | 子指标名称 | 所需数据信息 | 数据类型 |
|---|---|---|---|
| 速度控制 | 超速 | 自车速度 | 整型值 |
| 急加速 | 自车速度变化率 | 浮点数, | |
| 急减速 | 自车速度变化率 | 浮点数, | |
| 换道驾驶 | 转向灯使用情况 | 转向灯信号 | 布尔值 |
| 换道时间 | 换道驾驶模式数据段长度 | 整型值 | |
| 急转向 | 自车横向加速度 | 整型值 | |
| 换道间隙 | 自车与其他车辆的位置关系 | 整型值 | |
| 跟车驾驶 | 跟车过紧 | 刹车前1s的 | 整型值 |
分析一下上表中的各个数据。
超速
一个整型值大约区间在之间的数。
急加速/急减速
一个量级在之间的浮点数。
转向灯使用情况
布尔值,在转弯,变道时使用。或者。
换道时间
一个之间的整数。
急转向
一个整型数,大概也就在之间。
换道间隙
这个其实目前实际很难获取到,因为车与车之间目前还没有传感器探测相互车距。这里只做理想设定。采取当换道时超车与被超车之间的间隙。在实际路况中大概米之间吧。
刹车前1s的
是描述前后车辆关系的一个物理参数,常用来评价跟车过程中的前后车辆间的危险程度。其计算公式如下:
其中是两车的相对速度,单位为;是两车的相对距离,单位为; 的单位为
对于刹车前的项的识别需要的数据信息为自车速度,周围车辆速度及自车与周围车辆相对距离。这个也是在实际中难以获取的数。
以上的数据,是在实际开车中,感觉出来的。因为没有现实的数据。只能凭感觉设定一些数值。
设计算法
我们的最终目的是为了求得在一辆车在某一段路的安全行驶分数。这个分数反映了驾驶人在这段路的是否涉及危险驾驶。
通过以上的问题分析,准备设计一段程序,通过输入一组长度为的向量。输出得到一个的整型数,数字越高表示越安全,数字越低表示越不安全。
首先我们通过分组将速度控制、换道驾驶、跟车驾驶。分为三组采取不同的权重进行影响。三组。分别对应了。由于最后一组只有一项所以。其中
随后通过得到最后的分数。
其实以上就是一个3层的神经网络 也可以通过一组长度向量通过神经网络直接得到最后的分值。无论哪种方式我们都要得到一组权重,这有两种方式得到,一种是主观的方式,采用AHP算法。一种是客观的方式,通过大量的样本进行训练。因为我们并没有大量的样本,所以我们通过AHP算法进行权重的生成。
在此之前我们通过以上有些是布尔,有些是整型,有些是浮点数。我们的系统输入需要做些统一度量的工作,避免输入数值相差过大对输出造成影响。通常状况有以下这样几种 归一化方法:
1.最大最小法
最大最小法包括归化到区间和。
a. 归化到区间
b. 归化到区间
2.平均数方差法
其中是样本的均值;是样本的方差。
这里没有负值所以如果要归一化的话,肯定是采取归化到之间的。采用最大最小法。但是这样其实不是很好,因为车速至少是一个在之间的整数,而急加速与急减速是小数,就算使用了归一化算法,那么其值与整型归一化后的数值也相差太远。由于我们要采用AHP算法,这种算法是采用专家主观的去设定权重值,所以对输入数据的数值大小非常敏感。我们可以采用两种方式进行。
- 对表中每项进行阀值的规定,当超过一个阀值时,统计次数。
- 使用最大最小法对每项进行处理使得每个值都在再使用对其进行压缩使得数值相差太大。
函数将输入挤压到区间。
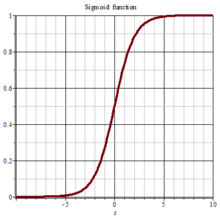
但是对输入大于小于之间的数,它将此挤压到之间。避免了诸如与这种情况数值影响。
使用次数作计算
- 间隔秒取一次当前车况状态。通过当前的状态计算出表中的数据。
- 因为分析到在实际路况中,偶然的违反以上的限定有时候是难免的。所以统计这段路以上过界的次数。以次数来反映整条路段的行驶状况,次数越少得分当然也就越高。
- 规定一个距离当到达这个距离时计算这个危险分数的分值。
- 可以在汽车停止后,平均所有个路段的分数,得出最后的分值。
- 由于车速这个值在不同天气状况以及不同路段是有不同的标准,所以需要汽车传感器在不同的情况进行统计。
- 由于交规中没有对一些数值进行阀值的规定,例如:超车间距,以及超车时间等。所以在实际系统中还需要涉及这些具体值的限定。
直接使用数值作计算
- 间隔秒取一次当前车况状态,通过当前的车况,只需要将数值传递给网络中进行运算,直接得出此路段分数。
- 由于这种直接取数值的计算,是当前秒的分数,所以这里可以分别间隔秒后取一次或者连续取秒并做均值。
- 在汽车停止后,平均所有个路段的分数,得出最后的分值。
- 由于车速这个值在不同天气状况以及不同路段是有不同的标准,所以需要汽车传感器在不同的情况进行统计。
在设计网络时,需要明确以下几个原则
- 车速,急加速,急减速 数值越大,越危险。分数就越低
- 是否使用换道时间越短、急转向数值越大、换道间隙越小 越危险。分数就越低
- 刹车前1s的越小,越危险。分数就越低
这两种方案,都有自己的好处,第一个实现比较简单,需要一些对于抓取的车况数据先进行预先处理。再进行运算。第二种不需要预运算,但是需要设计一个复杂的网络。这里我们使用第二种方案。原因没有实用角度,只是不喜欢预处理数据这部分。
这里再次说明一下。如果你有足够的样本 - 使用神经网络进行训练。这需要划分一下目标。因为是百分制而驾驶行为也是连续的,所以需要首先做下空间划分。以达到良好的映射关系。但是总觉得少了点什么。
如果没有样本,那么我的想法是使用算法进行人为的权重设定。也就是机器学习中所说的先验知识。依靠专家的知识进行权重的设定。
2012年中国高速公路事故信息 <- 我们所要依赖的专家知识
| 事故原因与形态 | 事故数比率 | 伤亡人数比率 | 财产损失比率 |
|---|---|---|---|
| 超速行驶 | |||
| 违法变更车道 | |||
| 制动不当 | |||
| 转向不当 | |||
| 油门控制不当 | |||
| 尾随相撞 | |||
| 同向刮擦 | |||
| 失速翻车 |
上表中尾随出事率很高,但是从驾车经验来看。 上表中应该是有交叉的。例如:跟车距离较近 + 超速行驶。单纯的超速应该不会有那么大的比率,用我们大CEO的話就是“快不代表不安全”。记得前几年朱哥哥从北京到天津全程只开了分钟,上次我和朱哥哥,文礼叔从北京到太原也只开了不到个小时。其实高速上快并不怕,怕是在快的条件下与前车的距离过近。
这里我们首先根据AHP算法进行划分。其次再进一步的设计网络。
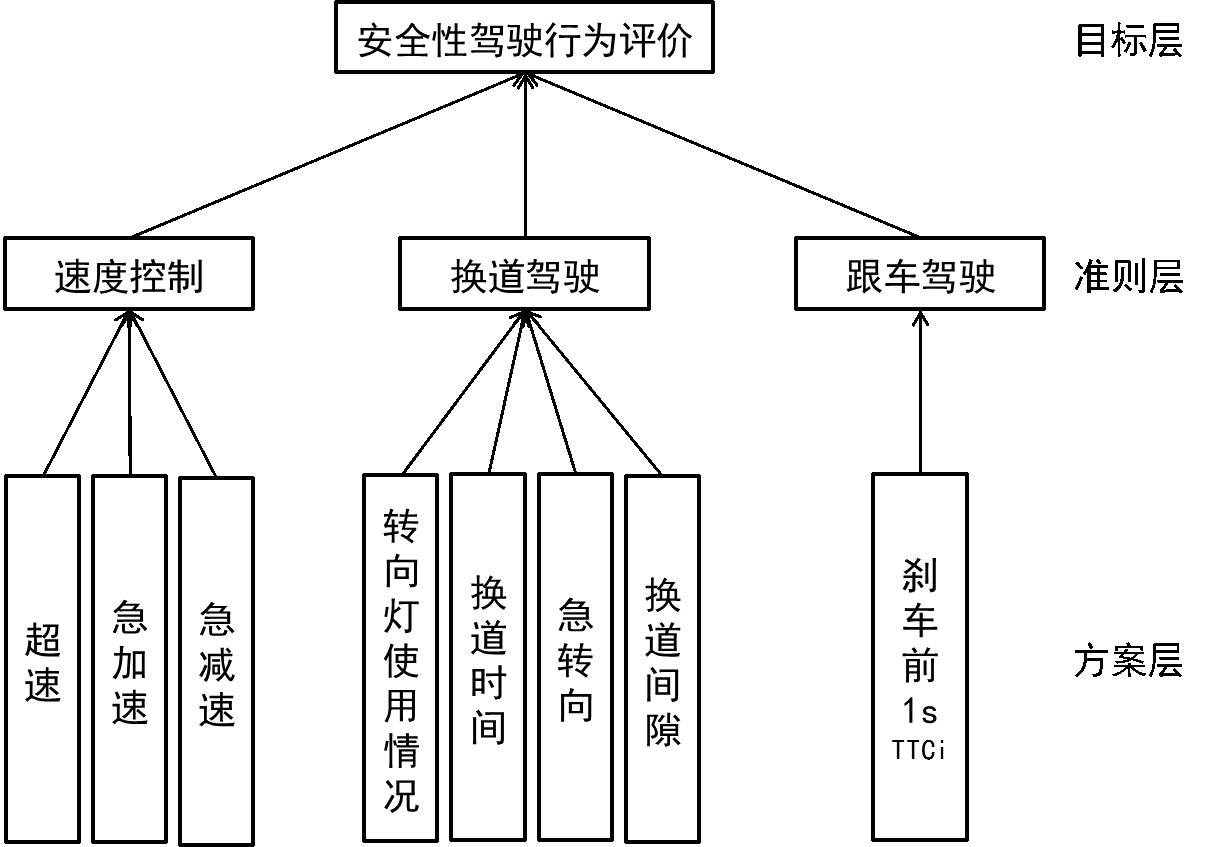
这里我们先设定一些变量如下表:
| 指标类 | 子指标名称 | 所需数据信息 | 变量名 | 对应权重 |
|---|---|---|---|---|
| 速度控制 | 超速 | 自车速度 | ||
| 急加速 | 自车速度变化率 | |||
| 急减速 | 自车速度变化率 | |||
| 换道驾驶 | 转向灯使用情况 | 转向灯状态 | ||
| 换道时间 | 换道驾驶模式数据段长度 | |||
| 急转向 | 自车横向加速度 | |||
| 换道间隙 | 自车与其他车辆的位置关系 | |||
| 跟车驾驶 | 跟车过紧 | 刹车前1s的 |
以上的权重是第一层网络的权重。第二层的权重是准则层的权重。
| 指标类 | 变量名 | 对应权重 |
|---|---|---|
| 速度控制 | ||
| 换道驾驶 | ||
| 跟车驾驶 |
通过三个值直接得出一个之间的数。
网络设计
我们有这样几个问题需要解决:
1. 归一化处理
2. 环境因素的影响,雪天,晴天对路况的影响
3. 最终得出的分值(百分制)
其中第二点环境的因素,主要是对车速的影响。这里我参照了两种状况:道路等级,光线等级。
| 道路等级 | 高速公路 | 隧道 | 省道 | 城市道路 | 乡村道路 |
|---|---|---|---|---|---|
| 限速(km/h) |
| 光线等级 | 晴天 | 阴天 | 雨天 | 雾 | 沙尘 |
|---|---|---|---|---|---|
| 能见度(km) |
我们首先要设计一层预处理层,就是对输入进行处理,其次再分别设计三个节点,接收三组数据。其中速度控制的网络中要结合道路等级以及光线等级两种值进行对车速的影响。这就还需要两个变量。其中表示道路等级,表示光线等级。并不是一个输入,而是参数。对最终车速的评定作出影响。那么速度控制这层又需要单独一层对车速最终的输出值进行计算。最后的评分函数,这个需要我们自己构造一个。能良好反映驾驶安全状况的。其中主层的权重通过AHP算法直接获得。
这就构成了我们的输入。
预处理层
这里并不对进行任何处理。应为输入总共有个元素,其中设预处理函数为
但是其中不对做处理,所以在其对应的位置设置为。这里也设定一个函数。
数值分析
其实是一个分段阀值。我们姑且想想汽车可以通过GPS信息结合地图信息获取当前道路情况并传递给我们。那么这里应该传递是当前路段的最高时速。这里因为是车速所以也直接同样做归一化处理,是能见度,当大于后,将没有任何限制,所以是一个取值的数值。这里做一下归一化处理直接除以得到一个之间的数。这里多一个函数专门来处理。
对输入向量进行预处理得到向量:
速度控制子网络
车速这个网络是最麻烦的,因为涉及到了两个参数。所以我们要将其考虑进去,因为速度控制有三个指标。超速的程度,急加速的程度,急减速的程度。这个参数只适用于超速的程度,能见度对三者都有影响,考虑在能见度较低的情况下,急加速减速的程度要越小。所以,要首先有个函数对是否超速作出判断,我们这里使用比例来解决,构造一个简单的函数,当超速时会提高自己的值。因为是一个小于的数字,而它的值越大,则表明速度越高,所以这里进一步构造
这样它越大,整个函数输出也就越小。对于急加速/减速也是相同的道理,这个值越大,最终得分也就越小,所以这里需要使用来减去这两个数值。这步做完之后,我们需要使用AHP算法来生成,最终通过,由于我们还要参考能见度。所以这里将其也考虑进去得到最终的输出。
换道驾驶子网络
转向灯状态,此值只有两个值,不需要做任何处理。 换道驾驶模式数据段长度,这个肯定是越大越好。 自车横向加速度,简单的通过来做减法。换道间隙,这个也是用来做减法。
这里不需要更多的分析,直接使用AHP算法生成权重得到最终输出
跟车驾驶子网络
只有一个数值,直接进行输出。
通过大量样本的机器学习与手工建模的区别,前者更加客观,但是需要大量样本来逼近最真实的情况。后者更主观,但是可以在缺少样本时使用。这里的模型也有做的不好地发,例如模型的预处理阶段使用了函数,而在速度控制中使用了简单的减去。但是实际是这个从的输入对应输出为之间,之间只有的差距。即便使用来做减法,其值差距也不是很高。但是当超速过快时,我们需要更突出过超更多时的部分。这就造成可能不能完全反映实际的情况。
评分层
这个层汇集了三个子网络的输出,通过AHP产生这三项相对重要程度的权重,最终得到一个输出,这个值应该是一个在之间的数。简单的使用来乘。得到的分数越高,则表示驾驶越安全。
接下来就是探讨如何生成权重的事情了。因为是主观确定,所以采用了AHP。下面简单探讨了AHP算法。
层次分析法(AHP)
首先说明的是以上的评测模型都是建立在一个叫做层次分析法的基础上的。简单的介绍下层次分析法。
层次分析法是是一种定性分析和定量分析相结合的方法。它通过分析复杂问题所包含的因素及其相互关系,将问题分解为不同的因素,并将这些问题归并成不同的层次,从而形成多层结构。在每一层次,按照一定准则对该层元素进行逐对比较,并按标度定量化
,形成判断矩阵。通过计算判断矩阵的最大特征值以及相对应的正交化特征向量,得出该元素对该准则的权重。在此基础上,可以计算出各层次元素对于该准则的比重。其具体实施步骤如下:
1 判断矩阵的构造
假设某个物体有个部分:,且,则表示第个部分相对整体而言比第部分重要的倍数,用表示,则可以得到如下矩阵:
其中矩阵中的元素具有如下性质:
则称矩阵为正互反矩阵。
定义1 判断阶为的方阵成立,则称满足一致性,并称为一致性矩阵。
定理1 一致性矩阵具有下列性质:
- ,且存在唯一的非零特征值,其规范化特征向量叫做权重向量;
- 的列向量之和经规范化后的向量就是权重向量;
- 的任一列向量经规范化后的向量就是权重向量;
- 对的全部列向量先求每一分量的几何平均,再规范化后的向量就是权重向量
指数标度的标度值和含义:
| 重要程度 | 数值 |
|---|---|
| 与同等重要 | |
| 比稍微重要 | |
| 比相当重要 | |
| 比强烈重要 | |
| 比极端重要 | |
| 比的重要性在上述描述之间 | |
| 比不重要的描述 | 相应标度的倒数 |
也可以使用一个的标准,这里用作为底,是从作为一个强烈范围
2 判断矩阵的一致性判别
文中采用"和法"来求特征根和特征向量,具体步骤如下:
- 将的每一列向量归一化得到
- 对按行求和得到
- 将归一化得到即为近似特征向量
- 计算,将其作为最大特征根的近似值。
然后根据一致性指标和随机一致性比率来判断矩阵的一致性,;,是对应指数标度的随机一致性比率。
3 专家信息的预处理
由定理1知,当为一致性矩阵时,,因此用与的偏差来检测判断矩阵的一致性是有效的。
用矩阵的最大偏差值和均方差来检验矩阵的一致性,最大偏差值和均方差的定义如下:
和的值越小,说明矩阵的一致性越好。
特征值与特征向量
因为在AHP算法中提到了特征值与特征向量,所以这里做一个简单的介绍。
将一个线性变换反复作用到一个向量,如果最终得到的结果可以表示为一个常量与这个向量的积,那么这个常量就是特征值而这个向量就叫做特征向量。
这个向量在数学建模中就是所谓的稳态向量。下边的一个例子取自《Linear Algebra with Applications》第七版中的一个例子。
某个城市中,每年有的已婚女性,且的单身女性结婚。假定共有名已婚女性和名单身女性,并且总人口保持不变,我们研究结婚率和离婚率保持不变时,将来长时间的期望问题。
为求得年后结婚女性和单身女性的人数,我们将向量乘以
年后结婚女性和单身女性的人数为
为了获得第年结婚女性和单身女性的人数,我们计算,一般地,对年来说,我们需要计算采用这种方法计算,并将它们的元素四舍五入到最近的整数。最终得到都是这个向量,假设输入初始值为,最终也会得到。
写段程序来证下。
import numpy as npfrom matplotlib.lines import Line2Dimport matplotlib.pyplot as pltfigure, ax = plt.subplots()ax.set_xlim(left=0, right=8500)ax.set_ylim(bottom=0, top=6500)A = np.array([[0.7, 0.2], [0.3, 0.8]])w = np.array([8000, 2000])for i in np.arange(0, 10):line = [(0, 0), (w[0], w[1])](line_xs, line_ys) = zip(*line)ax.add_line(Line2D(line_xs, line_ys, linewidth=1, color='blue', linestyle='-'))plt.plot()w = np.dot(A, w)plt.grid(True)plt.show()
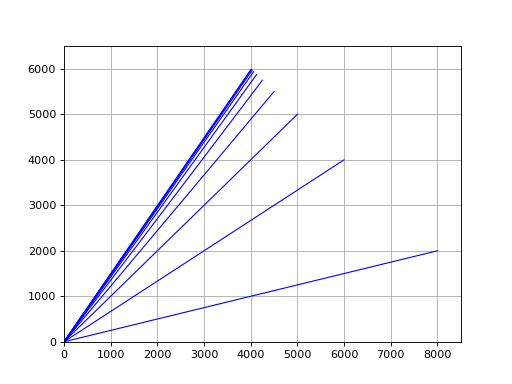
可以从上图中看出,向量逐渐收敛到
抛去深究为什么这个过程是收敛的,再看了以上的例子之后,让我们看一下其标准定义。
定义 令为一矩阵。如果存在一个非零向量使得,则称标量为特征值。称向量为对应于的特征向量。
按照上述定义的公式可以得出一个求得特征向量以及特征值的方法,上述公式可以写成
因此,为的特征值的充要条件是上述公式有一非平凡解,其解集为。如果为的一个特征值,则,且中的任何非零向量均为对应于的特征向量。子空间称为对应于特征值的特征空间。方程有非平凡解的充要条件是为奇异的,或等价地,
将上式子展开,我们得到一个变量为的次多项式,,这个多项式称为特征多项式。这个多项式的根即为的特征值。如果对重根也计数,则特征多项式恰有个根。可能有些会重复,有些可能是复数。
看一个例子:
求矩阵
的特征值和相应的特征向量:
解 特征方程为
展开以上行列式:,求这个方程得到和。这里尝试求得对应的特征向量,必须求的零空间。
最终求解得到,因此任何^T的非零倍数均为对应的特征向量,且为对应的特征空间的一组基。
求这个多项式,求得根后带入,再求的零空间即可得到特征值与特征向量但是这种算法不便于数值化,写程序也过有点复杂。这里我们再探讨得算法是取自一书中第七章第六节的一个算法。这里被称做为幂法。这节中还讨论其他的求特征值的算法。
就科普到这里吧!如果有兴趣的,本人强烈推荐《Linear Algebra with Applications》,现在貌似出版到第九版了。中文的翻译版本也超级好。线性代数方面的书买了三本,这本是我连续把第七版和第九版都买下来的并且全部读完的。课后习题大概做了一半。强烈推荐,里面不只是有一些理论。课后的习题以及其中例子都相当实用。这书也是我每年都要拿出来读两章的书籍。再次强烈推荐。
AHP算法实现
class ahp(object):"""层次分析法(1)将问题分解,建立层次结构;(2)构造两两比较判断矩阵;(3)由判断矩阵计算比较元素的相对权重;(4)计算各层元素的组合权重。"""def __init__(self):self.target_name = ""self.criterion_layer = Noneself.scheme_layer = []self.criterion_layer_weight = Noneself.scheme_layer_weights = []self.threshold = 0.1def judge_criterion_layer_consistency(self):cr = self.__judge_matrix_consistency__(self.criterion_layer)return crdef judge_scheme_layer_consistency(self, index):if index < 0 or index >= len(self.scheme_layer):raise ValueError("out of scheme layer range")cr = self.__judge_matrix_consistency__(self.scheme_layer[index])return crdef calc_criterion_layer_weights(self):self.criterion_layer_weight = self.__calc_layer_weights__(self.criterion_layer)return self.criterion_layer_weightdef calc_scheme_layer_weights(self, index):if index < 0 or index >= len(self.scheme_layer):raise ValueError("out of scheme layer range")v = self.__calc_layer_weights__(self.scheme_layer[index])self.scheme_layer_weights.append(v)return self.criterion_layer_weightdef __judge_matrix_consistency__(self, matrix):"""判断矩阵的一致性CR = \frac{\frac{\lambd_{max} - m}{m-1}}{RI}当CR等于0时,矩阵是完全一致性的"""# 阶小于等于30直接查表RI_n_30 = np.array([0, 0, 0.52, 0.89, 1.12, 1.26, 1.36,1.41, 1.46, 1.49, 1.52, 1.56, 1.58,1.59, 1.5943, 1.6064, 1.6133, 1.6207,1.6292, 1.6385, 1.6403, 1.6462, 1.6497,1.6556, 1.6587, 1.6631, 1.667, 1.6693,1.6724])# 计算矩阵的最大特征值以及特征向量# lambda_max = np.max(np.linalg.eigvals(matrix))lambda_max = self.__calc_matrix_max_eigen__(matrix)n = matrix.shape[0]if n == 1:return True"""当判断矩阵具有完全一致性时,CI=0CI越大,判断矩阵的一致性越差。注意当矩阵的n个特征值之和恰好等于n,所以CI相当于除最大特征值外其余n-1特征值的平均数"""CI = (lambda_max - n) / (n - 1)if n <= 30:RI = RI_n_30[n - 1]else:RI = self.__calc_rand_RI__(n)CR = CI / RI# 计算矩阵的最大特征值if CR < self.threshold:return Truereturn Falsedef __calc_layer_weights__(self, matrix):max_lambda, eigenvector = self.__calc_matrix_max_eigen__(matrix)return eigenvectordef __calc_rand_RI__(self, n=17, times=2000):"""计算高阶平均随机一致性指标(RI)"""A = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9,1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9])X = np.zeros([n, n])lambda_v = 0for num in np.arange(times):# 生成随机矩阵for i in np.arange(n):for j in np.arange(1, n):B = np.random.randint(0, 17, (n, n))X[i, j] = A[B[i, j]]X[j, i] = 1 / X[i, j]X[i, i] = 1# ev = np.linalg.eigvals(X)ev, _ = self.__calc_matrix_max_eigen__(X)lambda_v = lambda_v + evRI = (lambda_v / times - n) / (n - 1)return RI@staticmethoddef __calc_matrix_max_eigen__(matrix, epsilon=0.000000001):"""matrix 矩阵epsilon 误差使用幂法求最大特征值"""def __vector_normal__(vec):s = np.sum(vec)return vec / smax_lambda = 0eigen_vector = Nonen = matrix.shape[0]u_k = __vector_normal__(np.random.randint(1, 9, n))e = 1while e > epsilon:v_k = np.dot(matrix, u_k)abs_v_k = np.abs(v_k)max_index = np.argmax(abs_v_k)eigen_value = v_k[max_index]u_k = (1 / eigen_value) * v_kif max_lambda == 0:max_lambda = eigen_valuecontinuee = np.abs(max_lambda - eigen_value)max_lambda = eigen_valueeigen_vector = u_kreturn max_lambda, eigen_vector
判断矩阵
现在可以结合上2012年的高速公路事故表来制作判断矩阵了。我们先决定准则层。
通过AHP算法计算它的一致性是否满足。
接下来制作三个方案层的判断矩阵
判断其一致性。一致性通过,则计算出它们对应的权重向量(这也就是机器学习所说的先验知识)。
下表是判断矩阵对应的以及权重向量。
最终的程序实现
我们使用drive_info = np.array([70, 0.05, 0.05, 120, 15, 1, 4, 0.3, 3, 5])这个输入进行测试,最终得到得分为:
/home/devilogic/anaconda3/bin/python /home/devilogic/workspace/hkfiction/driver_model.py建立安全性评估[[ 1.00000000e+00 7.38905610e+00 4.03428793e+02][ 1.35335283e-01 1.00000000e+00 5.45981500e+01][ 2.47875218e-03 1.83156389e-02 1.00000000e+00]][+]criterion layer matrix is consistency(0.000000)criterion layer weight:[ 1. 0.13533528 0.00247875]--------------------[+]scheme[0] layer matrix is consistency(0.000000)[0]scheme layer weight:[ 1.00000000e+00 3.35462628e-04 6.73794700e-03]--------------------[+]scheme[1] layer matrix is consistency(0.047757)[1]scheme layer weight:[ 0.22633867 0.062539 0.02300681 1. ]--------------------[+]scheme[2] layer matrix is consistency(0.000000)[2]scheme layer weight:[ 1.]驾驶评分:65
代码
#!/usr/bin/python# coding:utf-8import numpy as npfrom ahp import ahpdef normal_min_max(x, x_min, x_max):return (x - x_min) / (x_max - x_min)def sigmod(x):return 1 / (1 + np.e ** (-1 * x))def f_prep(x, x_min, x_max):return sigmod(normal_min_max(x, x_min, x_max))def f_y(y):if y >= 15:return 1return y / 15def f_os(a, x):return 1 - (a / x) * adef f_s(x):return xdef handle_drive_info(di):v = np.array([f_prep(di[0], 15, 200), # 超速f_prep(di[1], 0.05, 1), # 急加速f_prep(di[2], 0.05, 1), # 急减速f_prep(di[3], 40, 120), # 道路等级超速限制f_y(di[4]), # 能见度等级f_prep(di[5], 0, 1), # 转向灯光使用情况f_prep(di[6], 1, 30), # 换道时间f_prep(di[7], 0.05, 1), # 急转向f_prep(di[8], 2, 200), # 换道间隙f_s(di[9])]) # 刹车前1sTTCireturn vdef subnet_speed(v, sw):x = v[3]y = v[4]res = np.array([f_os(v[0], x), 1 - v[1], 1 - v[2]])o = np.dot(res, sw)return y * odef subnet_change(v, cw):res = np.array([v[0], v[1], 1 - v[2], 1 - v[3]])return np.dot(res, cw)def subnet_follow(v, fw):return np.dot(v, fw)def score(subnet_outs, weight):out = np.dot(subnet_outs, weight)return 100 * outdef drive_score(di, ahp_obj):# 数据预处理info = handle_drive_info(di)subnet_speed_vector = info[0:5]subnet_change_vector = info[5::]subnet_follow_vector = info[8]a = subnet_speed(subnet_speed_vector, ahp_obj.scheme_layer_weights[0])b = subnet_change(subnet_change_vector, ahp_obj.scheme_layer_weights[1])c = subnet_follow(subnet_follow_vector, ahp_obj.scheme_layer_weights[2])outputs = np.array([a, b, c])s = score(outputs, ahp_obj.criterion_layer_weight)return sif __name__ == "__main__":"""研究汽车的安全指标性以及经济性----------------------------------安全性驾驶行为评价速度控制(speed control):超速急加速急减速换道驾驶(change lane):转向灯使用情况换道时间急转向换道间隙跟车驾驶(car following):刹车前1s的TTCi----------------------------------"""# 进行处理print("建立安全性评估")ahp_drive_security = ahp()# 建立准则层ahp_drive_security.criterion_layer = np.array([[1, np.e ** 2, np.e ** 6],[1 / (np.e ** 2), 1, np.e ** 4],[1 / (np.e ** 6), 1 / (np.e ** 4), 1]])print(ahp_drive_security.criterion_layer)if ahp_drive_security.judge_criterion_layer_consistency() is True:print("[+]criterion layer matrix is consistency")else:print("[-]criterion layer matrix is not consistency")ahp_drive_security.calc_criterion_layer_weights()print("criterion layer weight:")print(ahp_drive_security.criterion_layer_weight)# 建立方案层# 速度控制指标类对子指标层的判断矩阵ahp_drive_security.scheme_layer.append(np.array([[1, np.e ** 8, np.e ** 5],[1 / (np.e ** 8), 1, 1 / (np.e ** 3)],[1 / (np.e ** 5), np.e ** 3, 1]]))# 换道驾驶对子指标层的判断矩阵ahp_drive_security.scheme_layer.append(np.array([[1, np.e, np.e ** 2, 1 / np.e],[1 / np.e, 1, np.e, 1 / (np.e ** 3)],[1 / (np.e ** 2), 1 / np.e, 1, 1 / (np.e ** 4)],[np.e, np.e ** 3, np.e ** 4, 1]]))# 跟车驾驶对子指标层的判断矩阵ahp_drive_security.scheme_layer.append(np.array([[1]]))i = 0for m in ahp_drive_security.scheme_layer:print("--------------------")if ahp_drive_security.judge_scheme_layer_consistency(i) is True:print("[+]scheme[%d] layer matrix is consistency" % i)print("[%d]scheme layer weight:" % i)w = ahp_drive_security.calc_scheme_layer_weights(i)print(w)else:print("[-]scheme[%d] layer matrix is not consistency" % i)i += 1# 输入驾驶信息over_speed = np.array([120, 80, 70, 60, 40])drive_info = np.array([70, 0.05, 0.05, over_speed[0], 15, 1, 4, 0.3, 3, 5])print("驾驶评分:%d" % drive_score(drive_info, ahp_drive_security))else:pass
娜迦V5 2018

