计算物理第四次作业

未分类
作者：郭潇

---

摘要

采用Euler方法求解课本第一章的习题1.5,提供在一般情形下求解此问题的程序，并在文中给出在某一具体情形下的结果，之后分析了该解法求得的数值解与精确的解析解之间的差距大小与步长的关系。

背景介绍

此题的大意是讲有两种核A、B会相互衰变（或者说振荡）,用$N_A$表示A核的数目，$N_B$表示B核的数目，它们之间满足常微分方程组

$$\frac{dN_A}{dt}=\frac{N_B}{\tau}-\frac{N_A}{\tau}$$
$$\frac{dN_B}{dt}=\frac{N_A}{\tau}-\frac{N_B}{\tau}$$
求解在初值和各种参数给定的条件下，t时刻两种核的数目的函数关系。

正文

---

差分

用差分代替微分

$$\frac{N_A(i+1)-N_A(i)}{dt}=\frac{N_B(i)}{\tau}-\frac{N_A(i)}{\tau}$$
$$\frac{N_B(i+1)-N_B(i)}{dt}=\frac{N_A(i)}{\tau}-\frac{N_B(i)}{\tau}$$

迭代

整理上式得递推式

$$N_A(i+1)=N_A(i)+\frac{dt}{\tau}(N_B(i)-N_A(i))$$
$$N_B(i+1)=N_B(i)+\frac{dt}{\tau}(N_A(i)-N_B(i))$$
只要选定足够细的步长，根据这两个等式不断迭代，就可以逼近微分方程组的解析解，这里给出了求解此常微分方程组问题的求解程序代码的链接

输入初始条件

$N_A(0)=100$,$N_B(0)=0$,参数$\tau=1s$,步长$dt=0.1s$

输出结果

求解结果绘制如图，其中虚线是数值解法得到的结果，图中将其与精确的解析解（见后文）进行比较：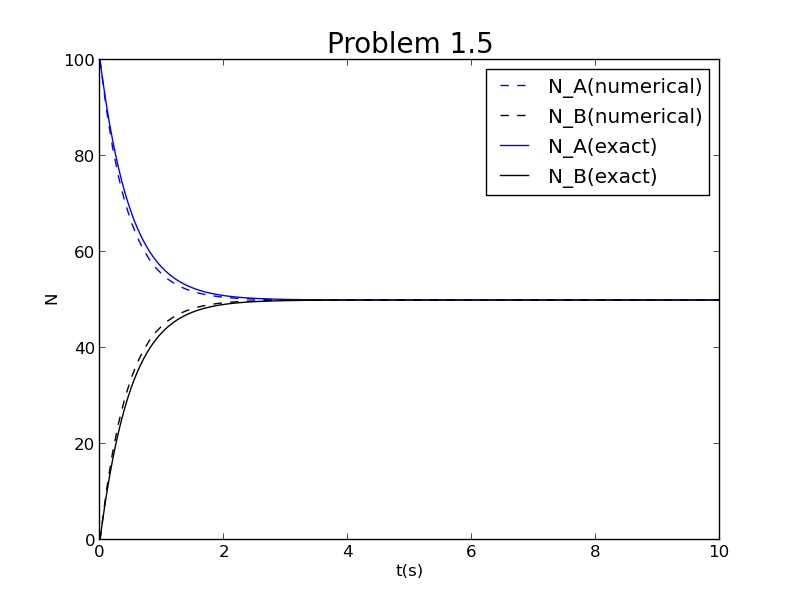
相应的数值解的数据保留在文档chapter1.txt里。
注：为确保精确解作图的连续性，我划分了400个点作出精确解的曲线，这是不随输入步长大小变化的，保证了精确解的曲线的精确性。

结果分析

该方程的解析解

$$N_A(t)=\frac{1}{2}(N_A(0)+N_B(0)+(N_A(0)-N_B(0))e^{-\frac{2t}{\tau}})$$
$$N_B(t)=\frac{1}{2}(N_A(0)+N_B(0)-(N_A(0)-N_B(0))e^{-\frac{2t}{\tau}})$$
由此解析表达式可求得方程的精确解，从而可以与数值结果相比较，得知数值解的精确度。
由上图可以看到：在0.1s的步长下，数值结果与精确解仍有一定的差距，为将差距定量化，后面又修改了程序，增添了对误差的定量分析并绘图，代码在此，输出数据在文档chapter1_error.txt中.
输入同样的数据，将数值解减去精确解得到的绝对误差绘制成下图

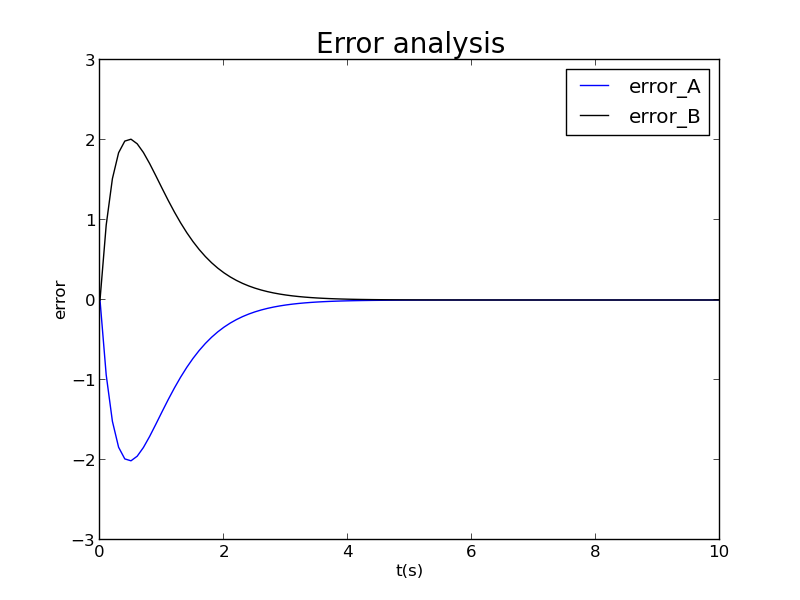
根据此图可以发现，随着迭代次数的增加，绝对误差先迅速增大后缓慢减小，最后收敛到零；观察数据可以得知，在$t=0.5s$附近误差的绝对值取得最大值，另外，在此步长下，绝对误差的绝对值基本不超过2（个）。注意：两种核的总数是100个。
为深入研究问题，利用以上的程序，下面又减小了步长，以逼近精确解

减小步长

$N_A(0)=100$,$N_B(0)=0$,参数$\tau=1s$,初始条件和参量均不变，减小步长使得$dt=0.05s$
得到结果如下图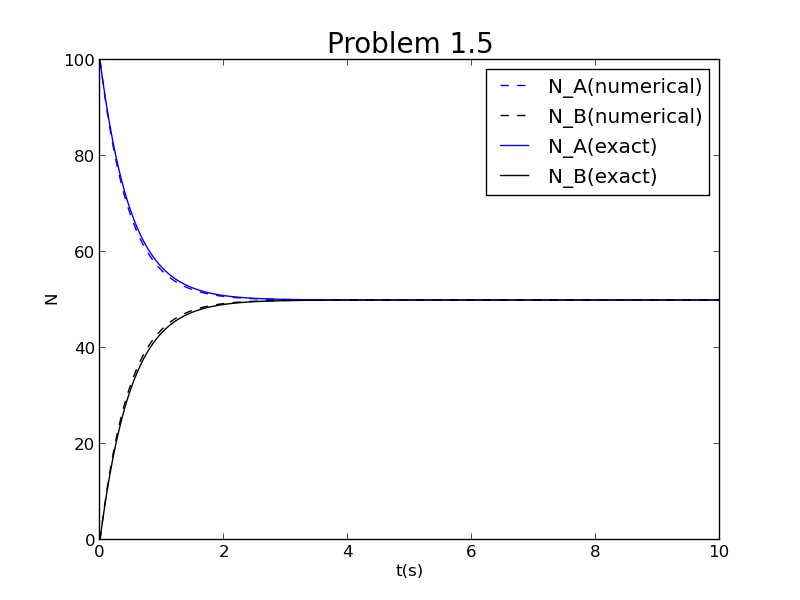
可以看到数值结果与精确解更加接近了，相差不多，定量地将此时数值解的计算误差绘制出来的图如下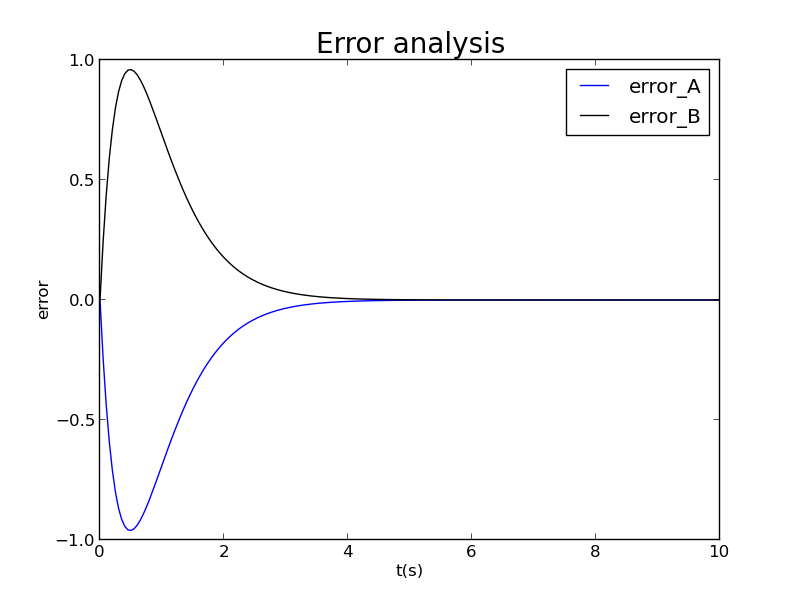
随迭代次数的增加，误差的大小也呈现类似的趋势（先起后伏，最后收敛到零）；在此步长下，误差的绝对值不大于1，大约是步长1s时的误差的一半。
还可以展示出$dt=0.01s$时的计算误差

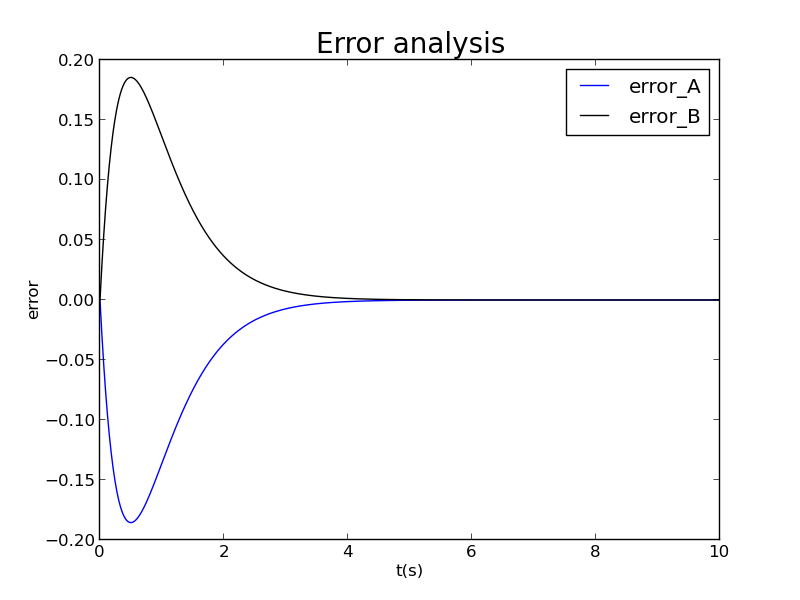
误差的绝对值不超过0.2
在同样的初始条件下，经过大量的计算可以发现，它们的误差都服从上述的规律。下面我通过数据定量分析误差的绝对值与步长之间的关系。

检验正比关系

在相同的初始条件和参数下，输入不同的步长dt（$dt\leq0.1s$)，然后选取每组中的最具有代表性的数据（即$t=0.5s$时计算误差取得的最大值）进行拟合，发现它们之间有良好的线性关系，如下图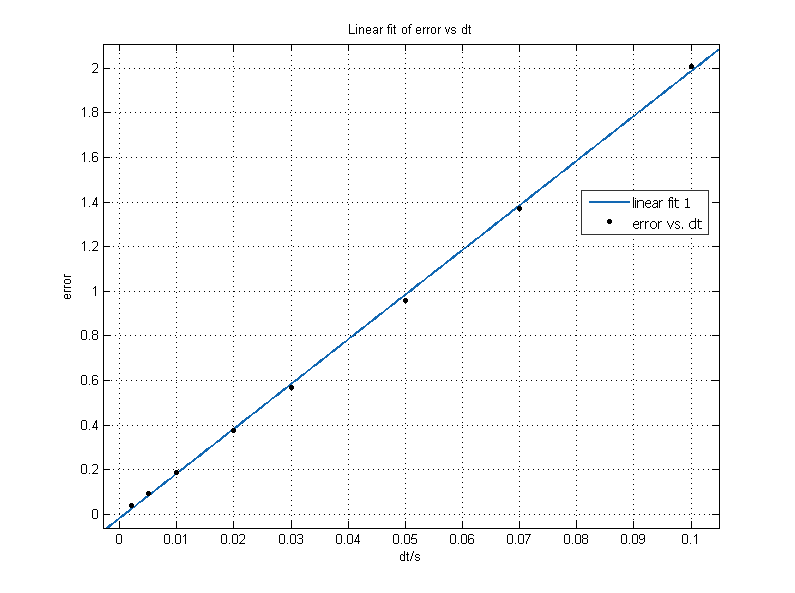
$R^2=0.9994$，线性相关度极高；纵截距-0.01987，几乎过原点，说明误差大小与时间步长之间几乎是成正比的。

结论

本文重点研究了$N_A(0)=100$,$N_B(0)=0$,参数$\tau=1s$的条件下，时间步长对计算结果的影响，得出以下结论：
①计算误差的大小随迭代次数的增加先迅速增大后缓慢减小，最后收敛到零，并在$t=0.5s$附近取得最大值。
②在各种参数都不变的条件下，计算误差的大小近似与步长成正比。

致谢

笔者在完成此稿之前阅读过陈锋与陈洋遥的作业，受到过他们的启发，还有感谢老师提供了原始程序的模版。