Lorenz Model

--The 10th homework
Author:GUO Xiao
Student number:2013301020099
chaos

---

Abstract

This article will research the chaos of Lorenz model.

Background

Lorenz was studying the basic equations of fluid mechanics, which are known as Navier-Stokes equations.These are a complicated set of differential equations that describe the velocity, temperature, density, etc. as a function of position and time.
A greatly simplified version of the Navier-Stokes equations as applied to a particular problem is only three equations:

$$\frac{dx}{dt}=\sigma(y-x)$$
$$\frac{dy}{dt}=-xz+rz-y$$
$$\frac{dz}{dt}=xy-bz$$

Solution

As usual,I use Euler method to solve these differential equations.Program code can be seen at the end of this article.

Results and discussions

1

Parameter $\sigma=10$,$b=8/3$
intial conditions are $x=1,y=z=0$
total time is 50, time step dt=0.0001
When $r=5,10,25$, $z$ as a function of $t$:

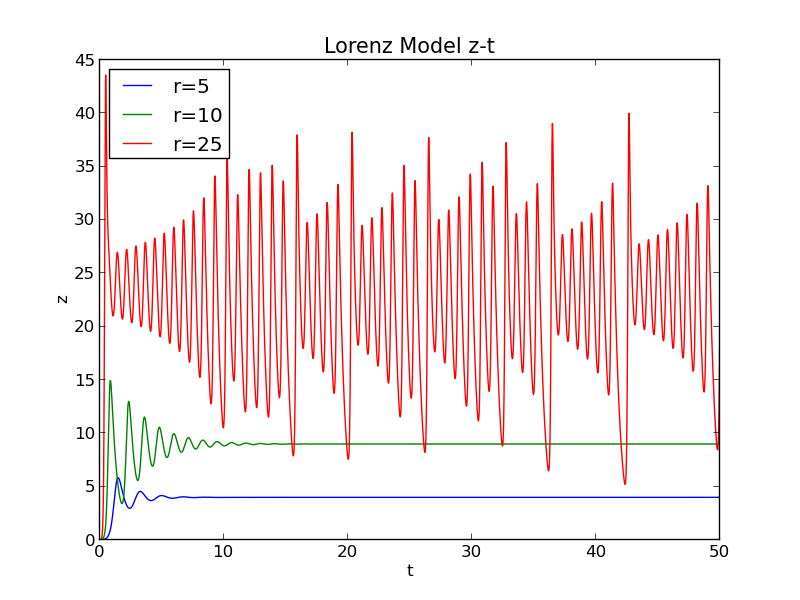
When r=5,10 it formed steady convection motion finally(blue line and green line);while r=163.8,it is chaotic (red line).

Corresponding Phase diagrams

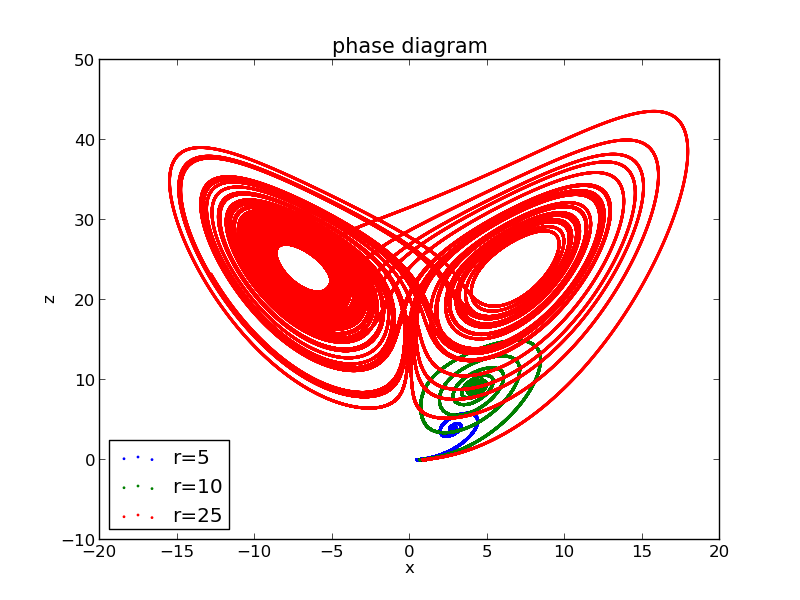
Different colors represent different r values.

3D phase diagram

When r=25,

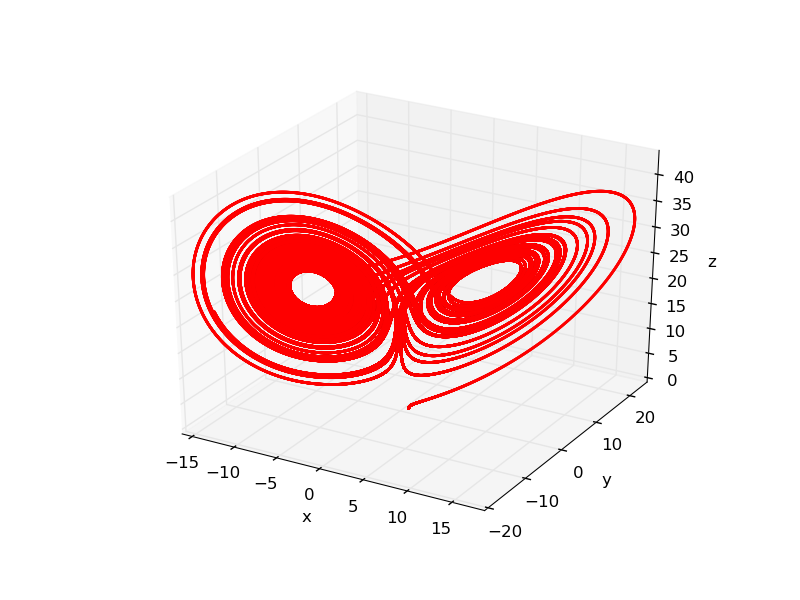
2

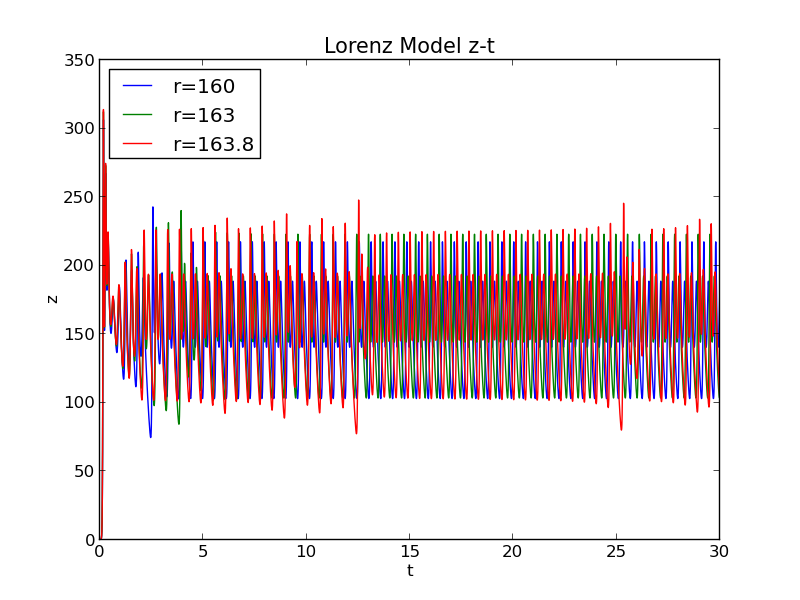
Fix other conditions,increase r value.
When r=160,160.3,163.8,z as the function of t are shown in following figure

Their phase diagram is

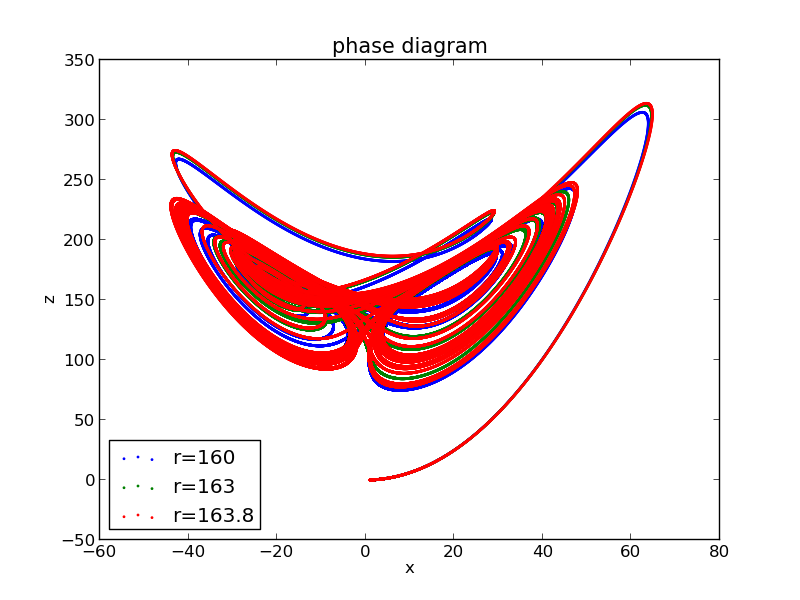
When r=160,163 it is periodic(blue line and green line)
while r=163.8,it is chaotic (red line)
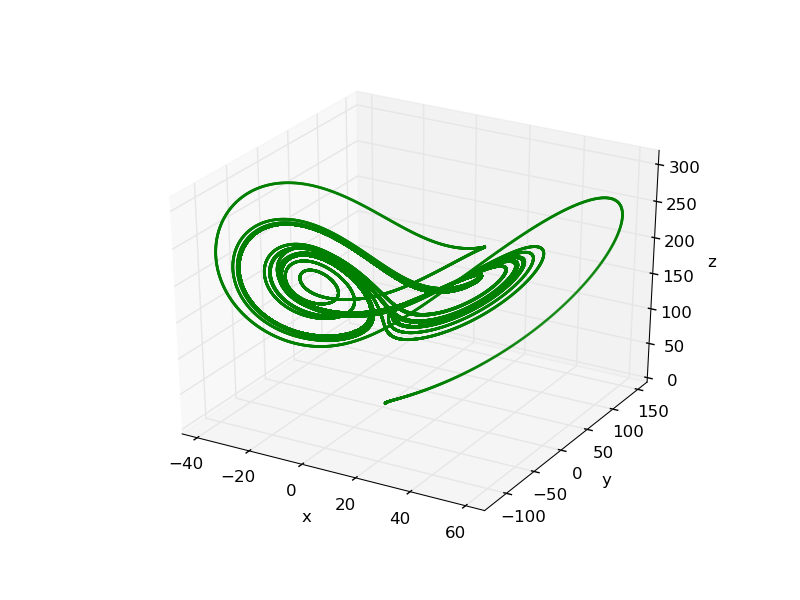
To observe it clearly,when r=163 its 3D phase diagram is shown in the following figure:

Bifurcation diagram

To reasearch the chaos between $r=163$ and $r=163.8$,I intend to plot its bifurcation diagram.

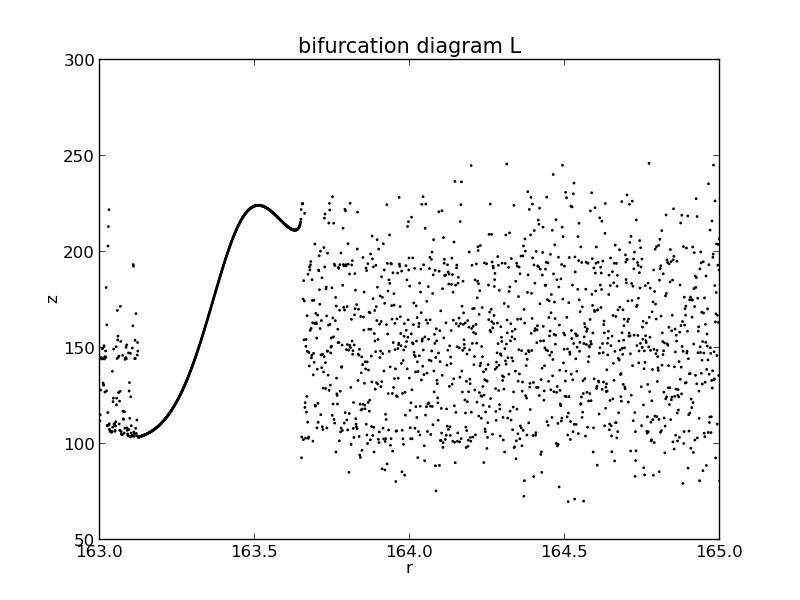
More detail about the transition to chaos are shown in the following figure:

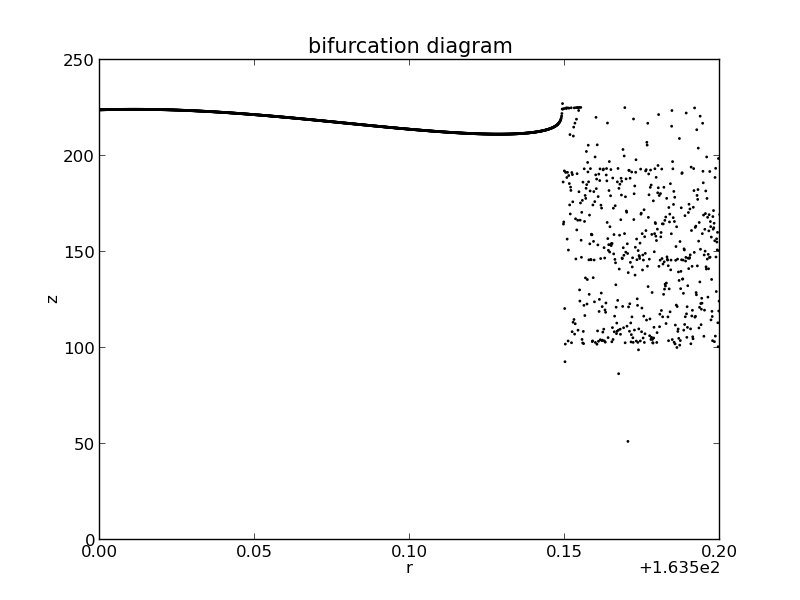
From the figure,we can see that the critical value of r is about 163.65.

Transition

When $r=163.65$,it is almost periodic.

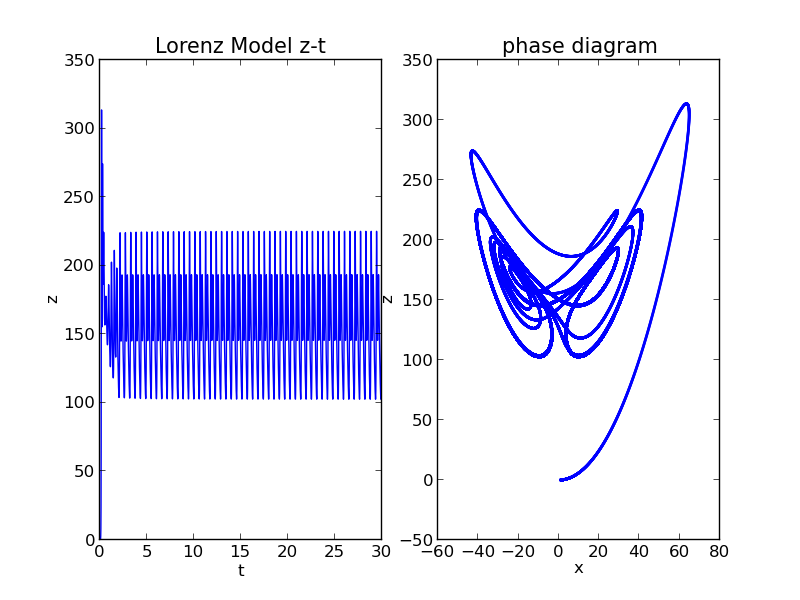
while $r=163.70$,it has become chaotic

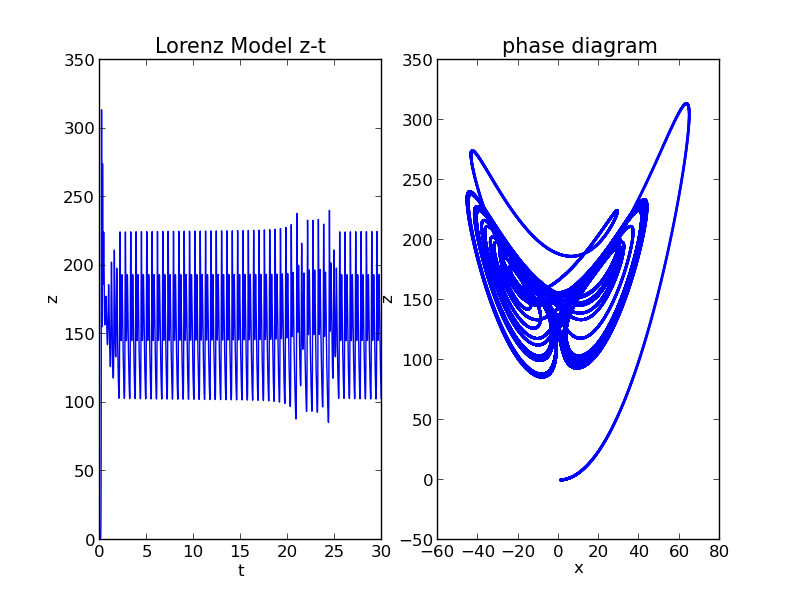
It is periodic in most regions,while it is chaotic in some areas.
Its phase diagram also tells us, it is intermittency chaos

Program code

Lorenz.py
bifurcation_L.py

Conclusions

• In general,system has a periodic behavior at small ,and will change to chaotic behavior as r is increased.
• $r\approx163.7$ is the turning point of the system to chaos by intermittency route.