@guoxiaowhu 2016-04-11T10:05:50.000000Z 字数 2719 阅读 2538

追溯球的轨迹Trace the Ball

————计算物理第七次作业

运动，力学

导读

凡是有过高中物理知识的人通常都会以为抛出去的球会在地球的重力下做抛物线运动，事实上真的是这样的吗？当然不是！！！事实上，由于球的旋转和空气阻力，再加上风的影响等等原因，使得球的实际轨迹往往出人意料，比如香蕉球、电梯球之类的，也使得球类运动更加精彩。设想一下若球的轨迹只是精准的抛物线，那么我们的球类运动也未免太单调了，下面就让大家来见识一下球的各种奇特的轨迹，绝不仅仅是抛物线哦！
网络图片

摘要

本文以棒球为例（因为棒球的运动比较复杂），建立数值的模型，计算了在特殊的初始条件下其运动轨迹
但结论不仅仅限于棒球，其他的球也可能有类似的结论。

背景介绍

设想我们抛出一个棒球，在抛出的时候给了它一个初速度，同时并使得它向后转如下图所示，于是在具有一个初速度 $v_0$ 的同时，还具有一个初始角速度 $\omega_0$ ，假设 $v_0$ 和 $\omega_0$ 都已知，下面建立接近实际的物理模型来求解它的轨迹。
插图1

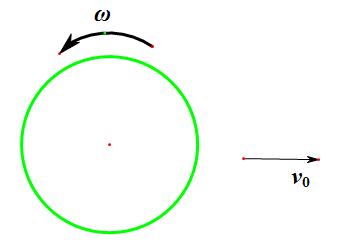
一、建立物理模型

首先分析球的受力，然后根据Newton第二定律建立起球运动的动力学模型。
重力当然必须要有，棒球的质量大约是149g。此外，还要考虑：

空气阻力（曳引力）

通常物体受到的空气阻力有如下关系式 $F_{drag}=-B_2v^2$ ， $B_2$ 是曳引系数（Drag Coefficient），负号表示它的方向与棒球的速度方向相反。
然而棒球的风洞实验却发现棒球的曳引系数是随棒球的运动速率而变化的，并且粗糙程度不同的棒球的变化曲线也不同，如下图所示：
插图2
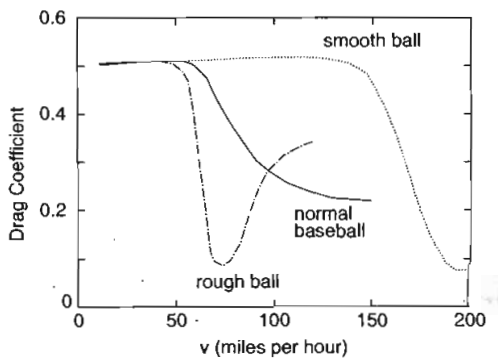
对于通常的棒球，它的曳引系数有如下经验关系式

$\frac{B_2}{m}=0.0039+\frac{0.0058}{1+e^\frac{v-v_d}{\Delta}}$
其中

$v_d=35m/s$ ,

$\Delta=5m/s$ ，并采用国际单位制(SI Units)

Magnus力

当物体在流体中移动并旋转时，由于物体不同部位流体不同，流体可能会对物体产生一个Magnus力

$\vec{F}_{Magnus}=S_0\vec{\omega}\times\vec{v}$

$S_0$ 是常数，

$\frac{S_0}{m}\approx4.1\times10^{-4}$
那么在上述的问题中，球受到的Magnus力的方向就是垂直于速度方向朝上的，如下图所示，请注意它的方向始终是垂直于速度的，就像磁场力一样。
插图3

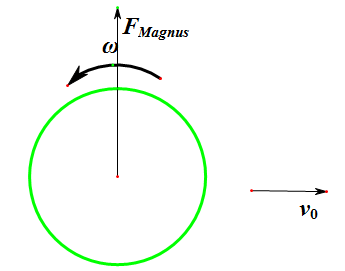
侧向力（Lateral Force）

然而众所周知，实际上的棒球并不是完美的球形，而是像下图这样的！！！

由于棒球的表面不同各处粗糙程度不同，各处受到的空气阻力也大小不一，总的效果是受到一个与棒球表面有关的侧向力，因为球的表面在旋转，这个力也会随之变化。
实验测得其大小变化随转过角度的关系如下图
插图4
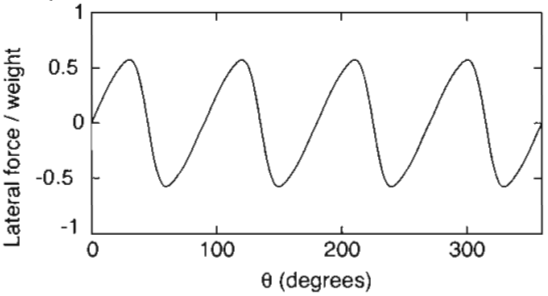
球在绕水平轴转，那么侧向力就应该是在竖直平面内并垂直于速度的。
可以给出其数值的近似表达式

$\frac{F_{lateral}}{mg}=0.5[sin(4\theta)-0.25sin(8\theta)+0.08sin(12\theta)-0.025sin(16\theta)]$
其中

$\theta=\int_0^t\omega{\rm d}\tau$

二、数值计算

建立坐标系，系统初始化

为方便起见，先设球从原点在 $xOz$ 平面内抛出,速度大小为 $v_0$ ，与水平方向夹角(仰角)为 $(90-\theta)$ °
建立三维直角坐标系如下图

动力学方程

结合以上几点，写出动力学方程如下

$\frac{dx}{dt}=v_x$

$m\frac{dv_x}{dt}=-B_2vv_x-S_0\omega v_z-F_{lat}\frac{v_z}{v}$

$\frac{dy}{dt}=v_y$

$m\frac{dv_y}{dt}=-B_2vv_y$

$\frac{dz}{dt}=v_z$

$m\frac{dv_z}{dt}=-mg-B_2vv_z+S_0\omega v_x+F_{lat}\frac{v_x}{v}$

$v=\sqrt{v_x^2+v_y^2+v_z^2}$
事实上，在上述初始条件可以得到

$v_y\equiv0$ ,所以y方向上的方程实际上可以被取缔。

数值计算

解决本题的程序是继上次作业计算炮弹的弹道的程序改编而来，点击这里可以看到上次作业的链接，采用类似的差分方法解常微分方程，先对速度进行差分迭代，然后将迭代后的速度代入位移的差分方程中，希望以此手续可以提高数值计算的精度。
据此使用Python语言编写好程序代码点击这里查看求解该题的程序的代码

计算结果

1

当球的转速较快时，用此程序输入初始条件 $\omega_0=2000$ rpm(转每分钟)， $v_0=49$ m/s，仰角0°，总时间10s，时间的计算步长 $dt=0.01s$ （确保计算的精度）,计算结果如下图所示
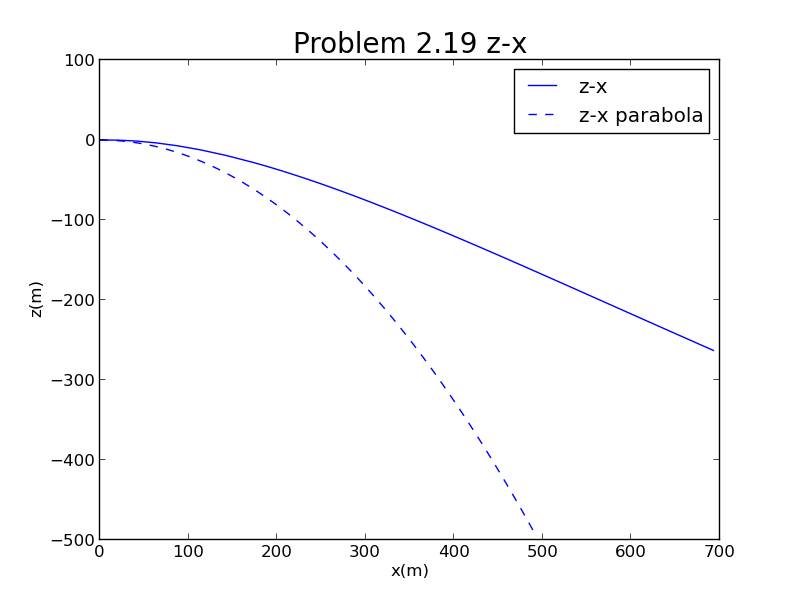w=2000 其中虚线代表相应的抛物线，实线代表球的实际轨迹，可以看到由于转速较大，Magnus力起到明显作用，使得曲线明显向上偏离抛物线，并越偏越远。
倘若将总时间延长至20s,像下图所示，球甚至有向上运动的趋势：
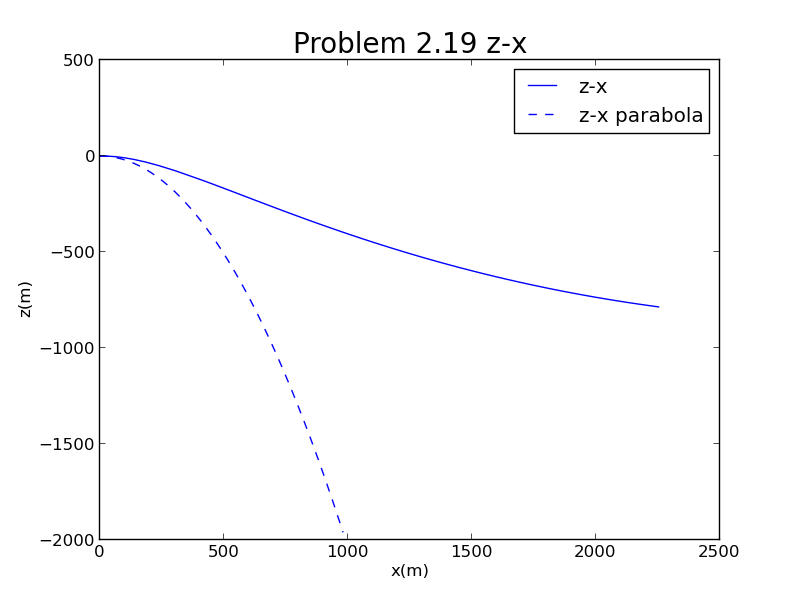
time=20s

2

倘若使得角速度 $\omega$ 反向,那么此时Magnus力将会向下，输入 $\omega_0=-2000$ rpm，其他条件不变，结果如下图
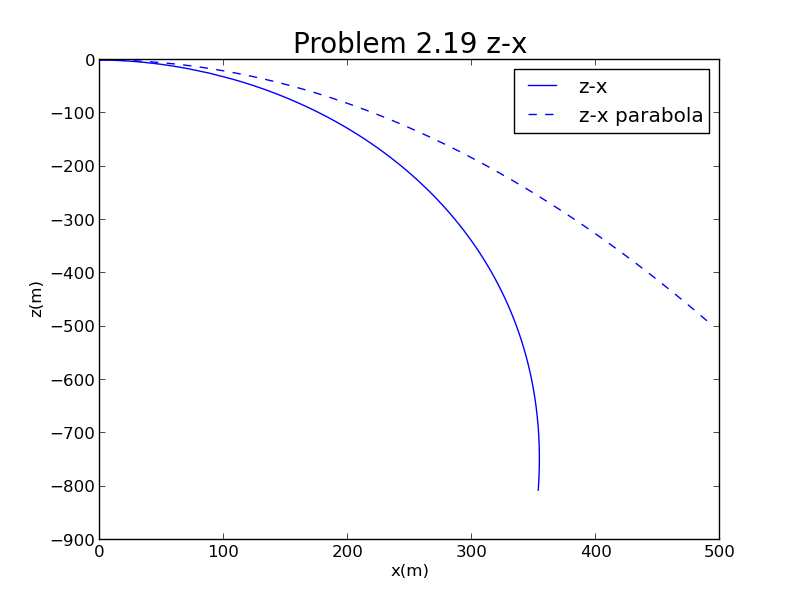
w=-2000
果然轨迹向下偏离抛物线，甚至会往回旋。

3

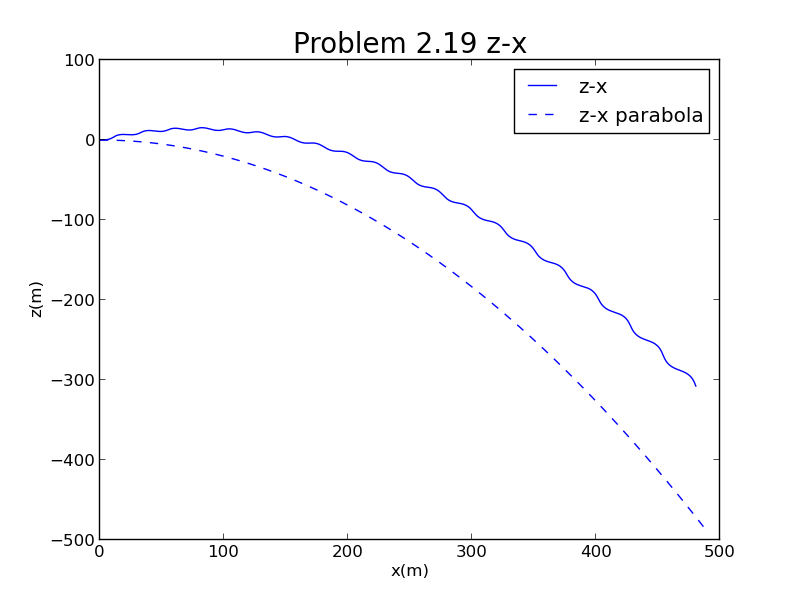
之前转动的角速度相当大，周期性变化的外力的作用被平均之后就没有体现出来。
而当角速度很小时， $\omega_0=20$ rpm，周期性的侧向力的作用就体现了出来，球在周期性变化的侧向力作用下发生上下抖动
w=20

深化

当然，如果仔细观察的话，你会发现上述几张图几乎是都不会发生在实际过程中的，毕竟棒球通常不会从那么高的地方落下来，因此通常人们也不会将棒球水平抛出，因此笔者修改了一下程序，将总时间不再作为输入的参量，而代之以一个while循环来判断球是否在地平面以下从而结束循环。（忽略人的高度）

4 改变发射角度，实际情形

选取一个典型的发射角：仰角45°， $\omega_0=2000$ rpm，并把横纵坐标比例调至1:1如下：
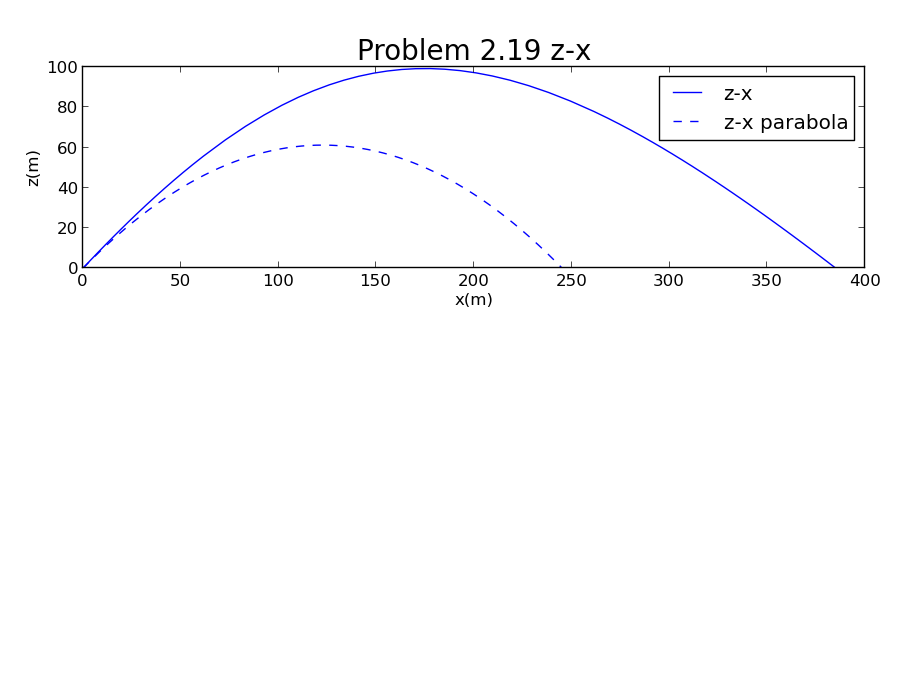
45degree
射程可达385m，而同样条件下理想的抛物线的射程只有不到250m，可见球向后旋转可以增大其射程，而且在 $\omega_0=2000$ rpm转速的时候效果很显著。
同时仔细观察可以发现由于空气阻力的不对称性使得球的轨迹不对称性。

拓展

后续还可以改变旋转方向，例如在水平面旋转，得到更复杂的三维运动图形

结论

当球的转速小的时候，侧向力（lateral force）起到明显作用，使其轨迹发生抖动；
当球的转速较大的时候，Magnus力起到明显的作用，使得其轨迹偏离抛物线，同时球向后旋转可以增大其射程。

参考文献

[1]N.J. Giordano,H. Nakanishi.Computational Physics(second edition)（影印版）.清华大学出版社