Research of Nonlinear Pendulum

---

The 8th homework of computational physics
Author:Xiao GUO
nonlinear,pendulum

---

Background

As we know,when the amplitude of a single pendulum is small,$sin\theta\approx\theta$,its motion can be approximately described by peroidic simple harmonic motion.

The famous conclusion summarized by Galileo is that the period of pendulum is independent of its amplitude.
However,what is real fact like problem 3.8 if we don't do this approxiamtion ?

Abstract

Author used Euler-Cromer method to solve the differential equation of nonlinear pendulum without approxiamation $sin\theta\approx\theta$.Thus find the real relationship between amplitude and period.

Physical Model

The result force of the single pendulum is shown in following figure:

According to Newtonion Second Law,we can get the equation of motion of a single pendulum without friction and driving force:

$$\frac{d^2\theta}{dt^2}=-\frac{g}{l}sin\theta$$
When $\theta$ is very small,$sin\theta\approx\theta$,this equation can be substituted by a linear differential equation $\frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta$.The solution of this linear equation is $\theta=Acos(\omega t+\phi)$, $\omega=\sqrt{\frac{g}{l}}$,it is exactly sinusoid and its period is independent of amplitude,so we can compare nonlinear pendulum with it.

Numerical Solution

In order to solve the nonlinear equation,firstly,transform this 2-order differential eqution into two 1-order differential equations:

$$\frac{d\omega}{dt}=-\frac{g}{l}sin\theta$$
$$\frac{d\theta}{dt}=\omega$$
Next,make them discrtization so that transform them into iteration formula:
$$\omega(i+1)=\omega(i)+dt(-\frac{g}{l}sin(\theta(i)))$$
$$\theta(i+1)=\theta(i)+dt\omega(i+1)$$

Solution Program

There is the link of the program code to solve this problem
After inputting relevant parameters,this program can calculate,print and store results and data,finally plot angle-time image and its phase diagram.

Results

Fix initial conditon $\omega_0=0$ and pendulum length $l=1m$
and time step $dt=0.01s$(sometimes $dt=0.001s$)
Just imagine that we set free the pendulum from angle $\theta_0$ without initial speed

1.

When $\theta_0$ is small, for instance,$\theta_0=10$degree

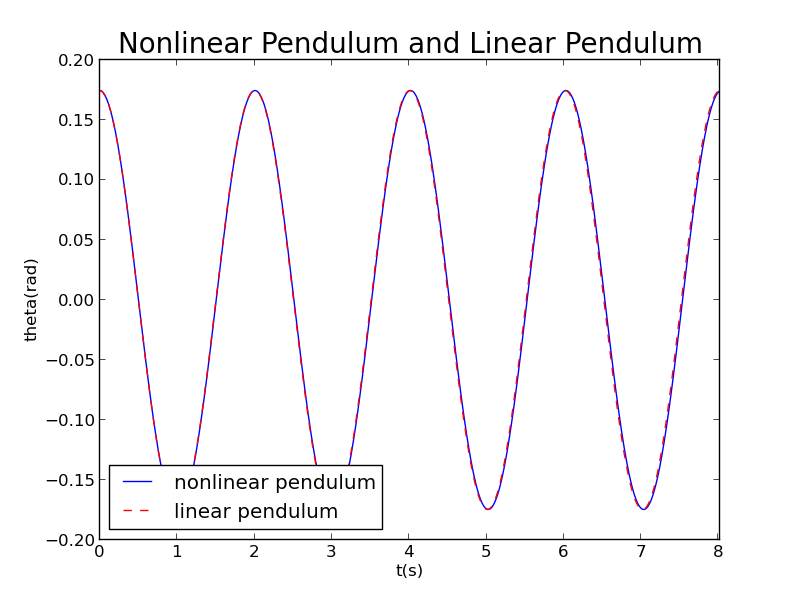
The curve of nonlinear pendulum is well consistent with sinusoid curve.
Attention:In these figures,the unit of $\theta$ is rad, not degree

2.

If we increase $\theta_0$,when $\theta_0=20$degree,

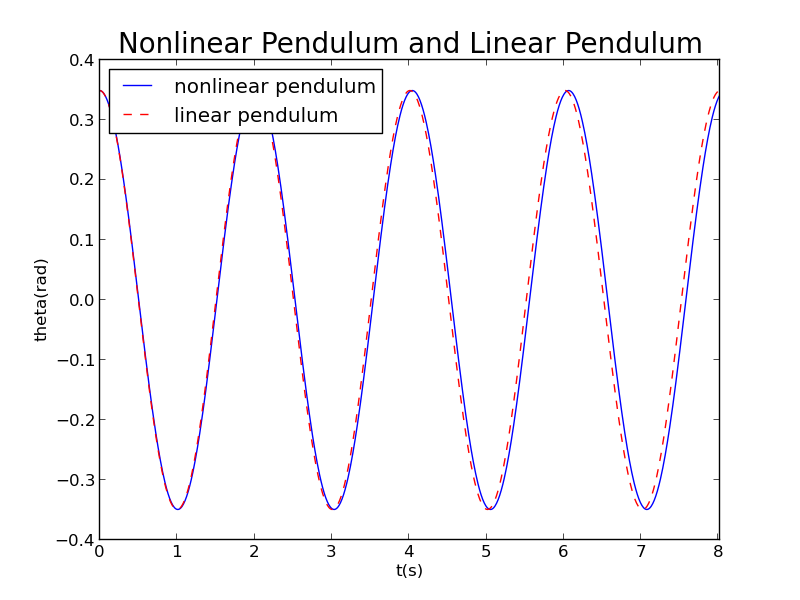
We can observe a little difference between nonlinear pendulum and linear pendulum.And the difference is accumulative with time goes by.Under this conditioin,the period of nonlinear pendulum is a little larger than before.
when $\theta_0=50$degree,

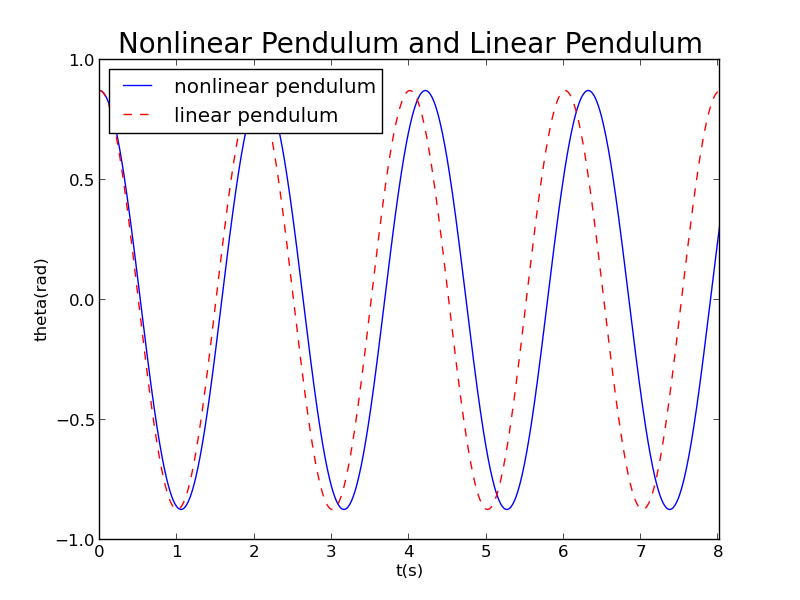
when $\theta_0=90$degree,attention:to see more periods of nonlinear pendulum, the magnitude of t axis multiplied by 2 in following figures.

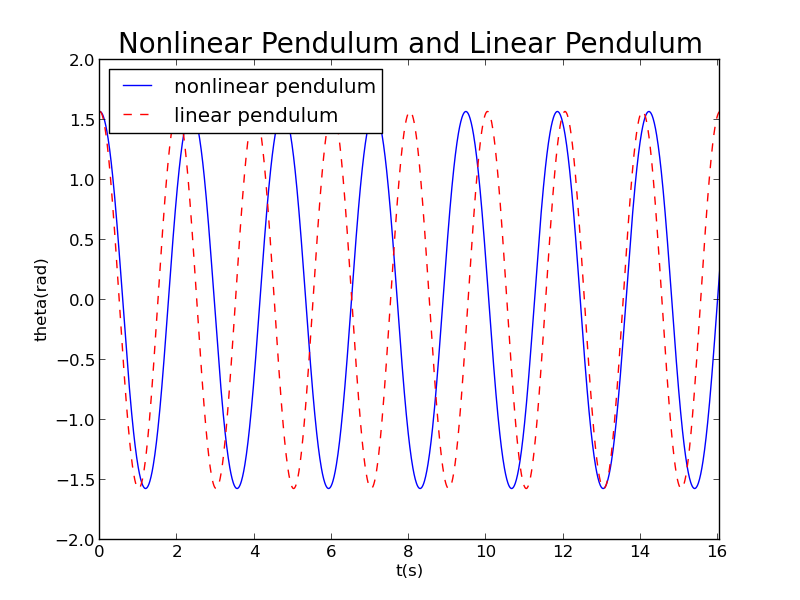
when $\theta_0=120$degree,

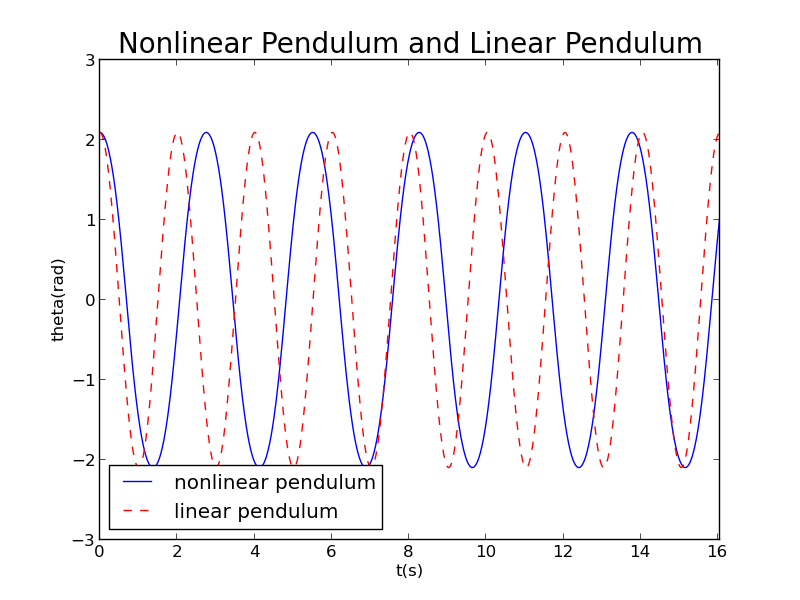
We can see that period of nonlinear pendulum increases with increasing amplitude.

3.

When $\theta_0$ approaches 180degree or -180degree,not only its period will be larger than period of other $\theta_0$,but also its qualitative shape will have great change.
When $\theta_0=179$degree

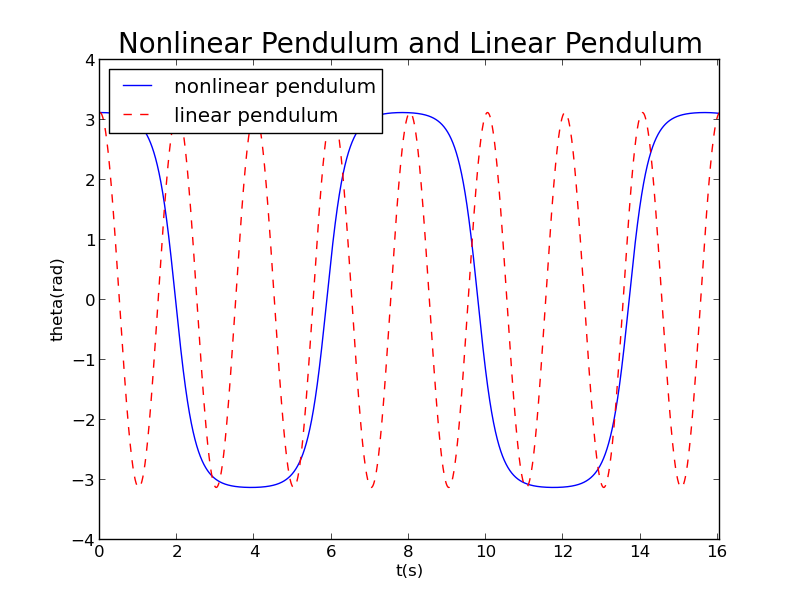
We can see that when pendulum reach the neighborhood of $\theta=180$(or$-180$)degree,its angular speed and acceleration is very small. The curve in these neighborhoods become almost horizontal and forms many platforms like the Great Wall, which is obviously different from linear pendulum.This difference can be also observed from its phase diagram.

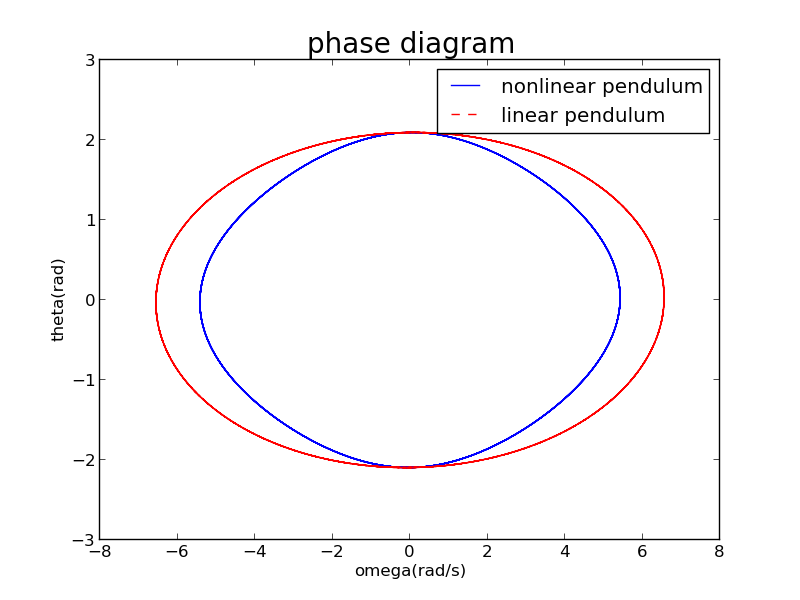
This figure shows that the phase trajectory of linear pendulum is an ellispe,while nonlinear pendulum's isn't.
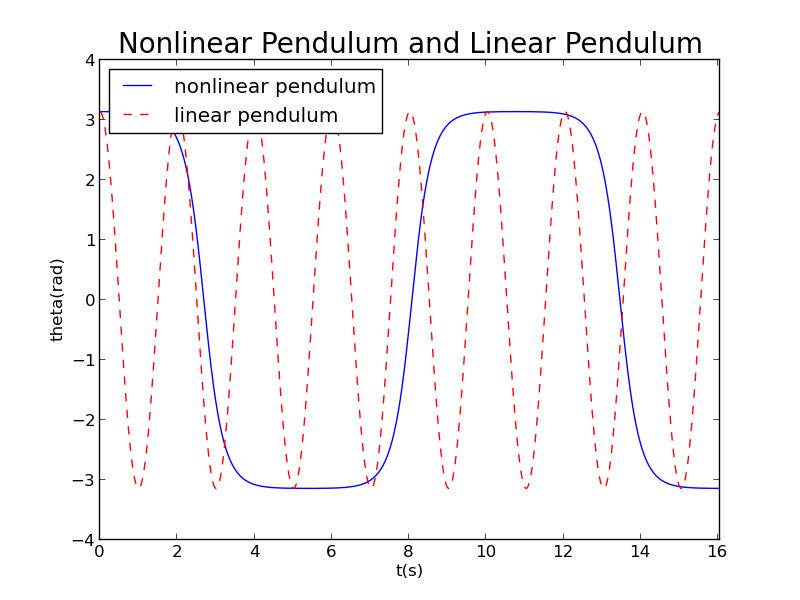
If $\theta_0=179.9$degree, this change of shape will be more obvious:

Its phase diagram:

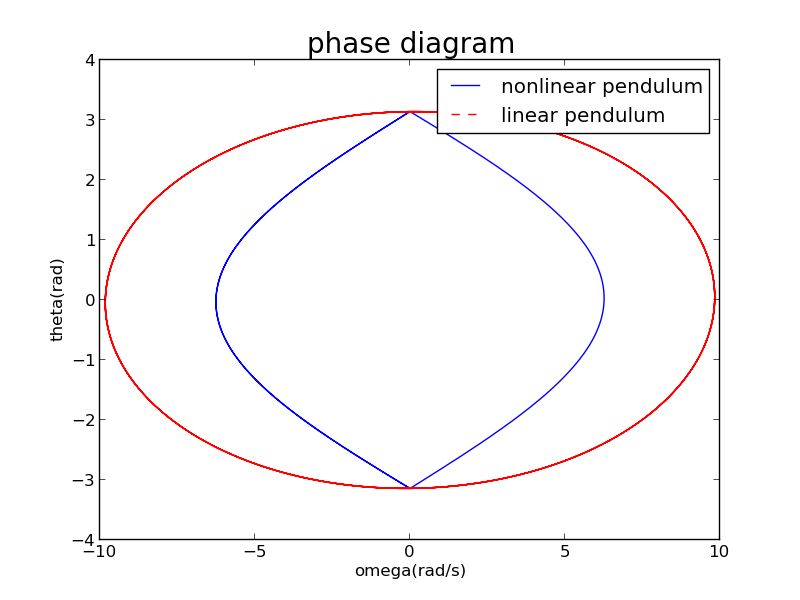
At the same time,we can see that a little difference in initial condition leads to great change in phase trajectory.

The Quantitative Relationship Between Amplitude and Period

Using previous program code to find out the quantitative relationship between amplitude and period.Following picture is the quantitative relationship between amplitude and period.

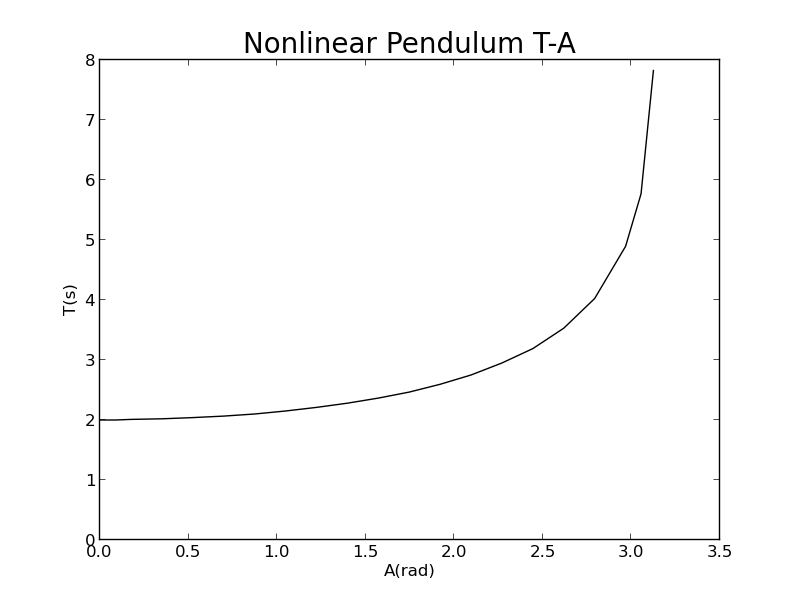
The period of linear pendulum is about 2s.

Extension

More interesting stories will happen if we set it free from a high angle$\theta_0$ with a enough initial speed so that it can rotate a whole cycle.
For example,
$\theta_0=179$degree
$\omega_0=-1$rad/s

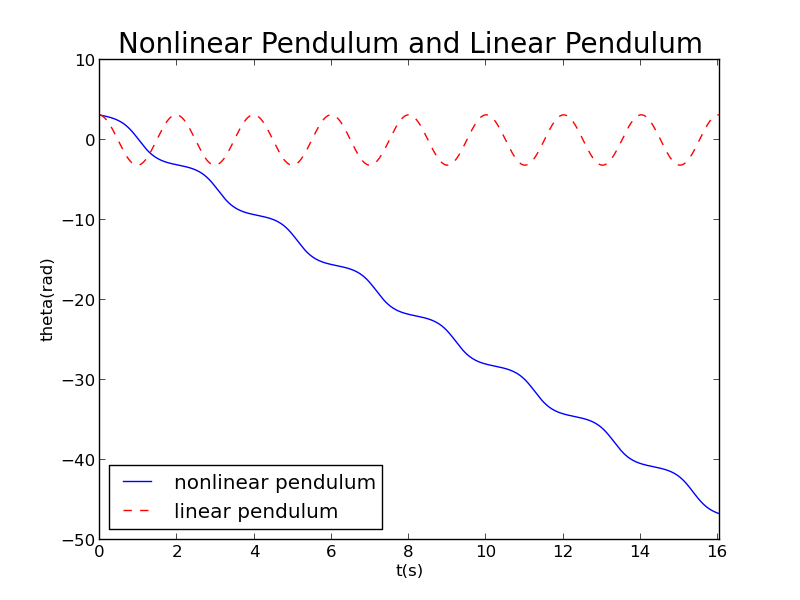
Its phase diagram:

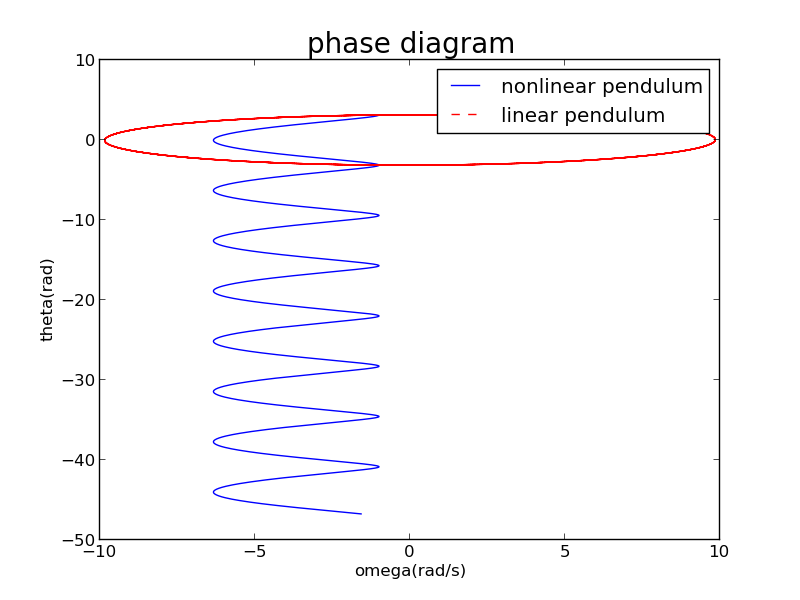
Attention:The period of theta is 2$\pi$.

Conclusions

• 1.The period of nonlinear pendulum increases with increasing amplitude, and its increasing speed is faster and faster.My article showed the quantitative relationship between amplitude and period.
• 2.When $\theta_0$ approaches 180degree or -180degree,its speed and acceleration is very small,so forms a platform.At the same time, its phase diagram is well different from that of linear pendulum.

Reference

[1]N.J. Giordano,H. Nakanishi.Computational Physics(second edition)（影印版）.清华大学出版社