Chaotic Physical Pendulum

--The 9th homework of Physcis
Author:GUO Xiao
nonlinear,pendulum

Beautiful Chaos

---

Abstract

Chaos is a complex phenomenon and it has many interesting properties.This article will investigate some interesting properties of chaotic phenomena by research of physical pendulum.

Introduction

Physical pendulum is a nonliear,damped,driven pendulum.It approaches the actual pendulum most.Because of its nonlinearity,the system can show many interesting chaotic behaviors.

Equation

The equation of a nonliear,damped,driven pendulum can be written as

$$\frac{d^2\theta}{dt^2}=-\frac{g}{l}sin\theta-q\frac{d\theta}{dt}+F_Dsin(\Omega_Dt)$$
$-q\frac{d\theta}{dt}$ is frictional force;
$F_Dsin(\Omega_Dt)$ is periodic driven force.
It is a nonlinear, 2-order ordinary differential equation,so it just can be solved by numerical method.

Solution

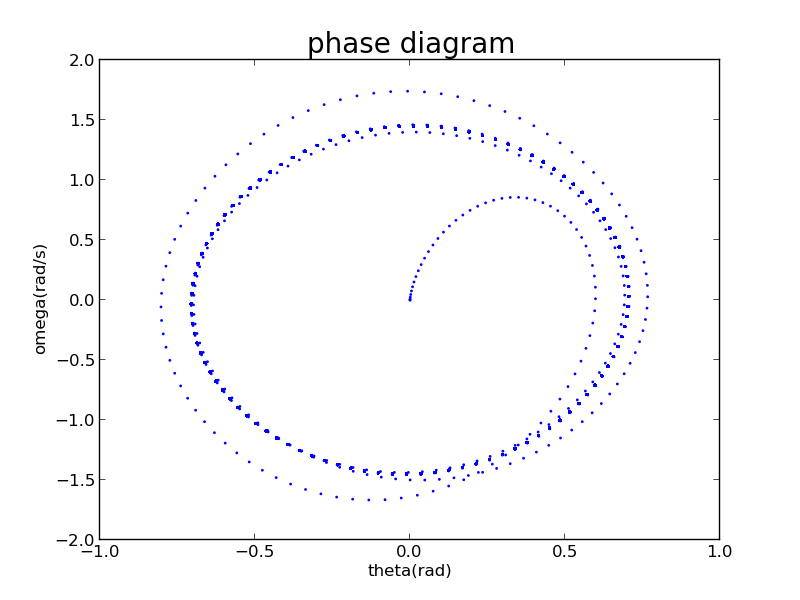
Utilize Euler-Cromer method to solve it, and plot its phase diagram to prove that the system can be chaotic.
Corresponding solution program code

For example,when $F_D=9$,$\omega_D=2$,$q=1$
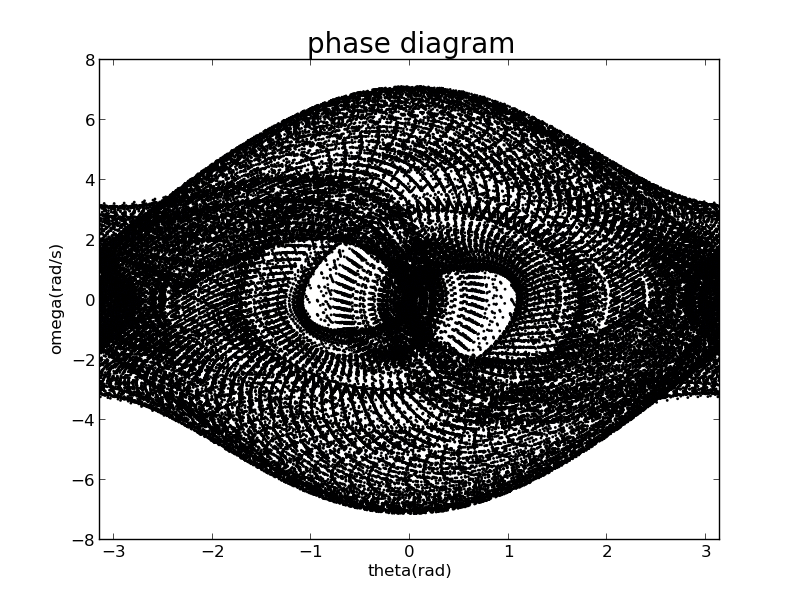
Its phase diagram

It is very dense,and almost full of whole graph.

Bifurcation Diagram

To learn about the global properties of this nonliear system,I need to draw its bifurcation diagram.

Program Code

Fix other parameters unchanged,change $F_D$,and fetch theta value of 400th period of driven force under every different $F_D$,then plot bifurcation diagram.
This is the link of corresponding program code to draw the bifuracation diagram
By the way,it tooks many hours to run this program and obtain final results!

Results

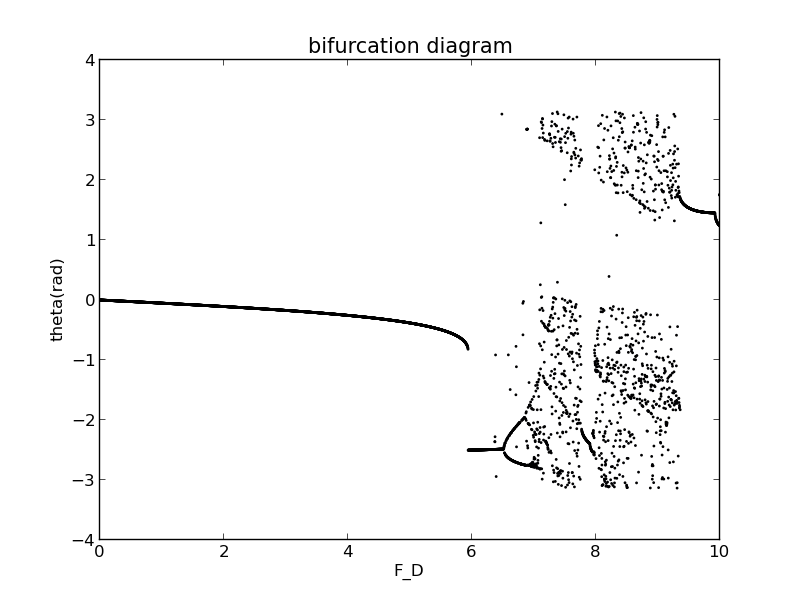
When $F_D$ varies from 0 to 10,We can acquire the following bifurcation diagram:

Magnify its horizontal axis scale,let $F_D$ varies from 5 to 10:

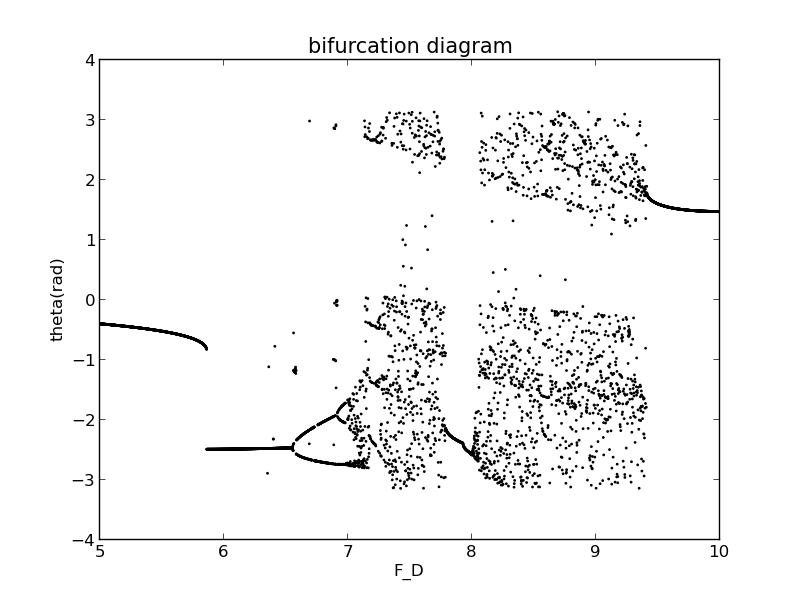
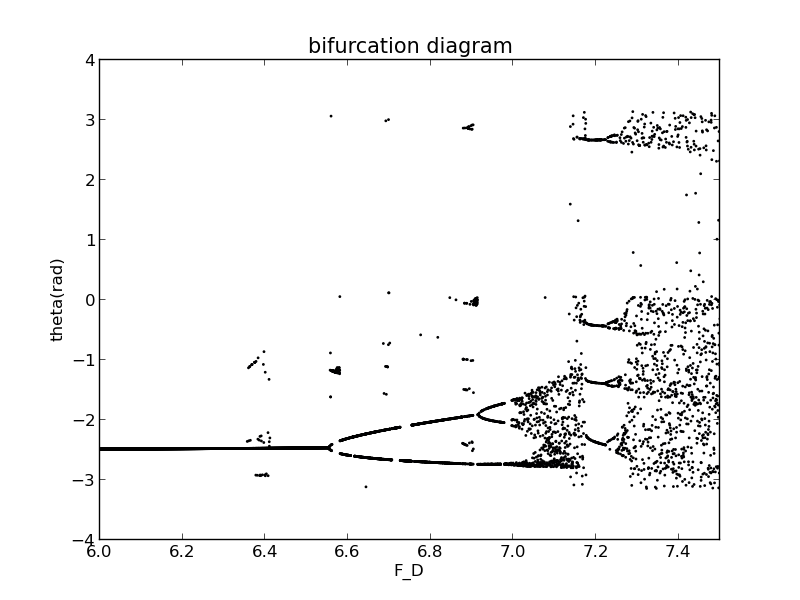
Magnifying its horizontal axis scale again we can find that the bifurcation digram has many fractal structures.

Verify the Bifurcation Diagram

1

According to the bifurcation diagram,we can know when $F_D=7.4$,the system is completely chaotic.

Under this condition, its phase diagram obtained by calculation is indeed completely chaotic as shown in following graph!

It phase trajectory is dense,quasiperiodic,unclosed and is alomst full of the whole figure.

Its Attractor

To obtain its attractor, I edited a new program to acquire theta value of every period of driven force.
corresponding plot program code

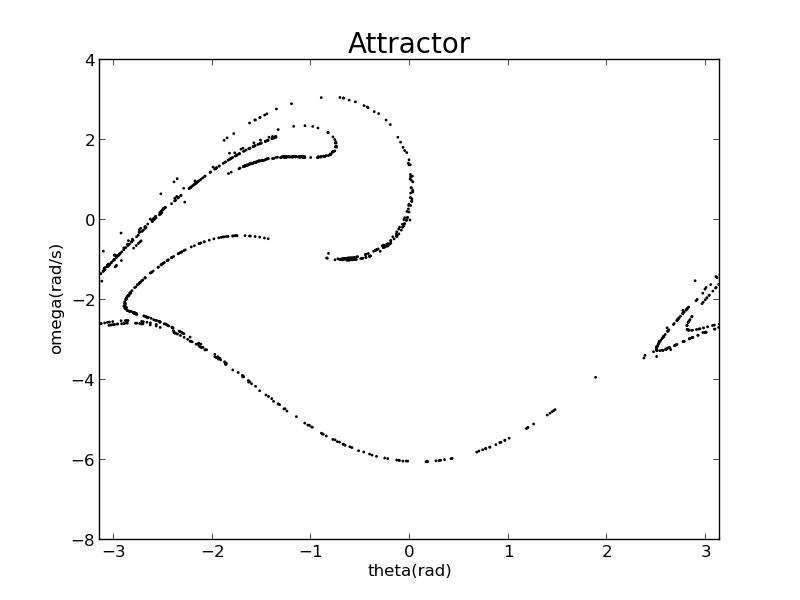
Dense points form some lines.

2

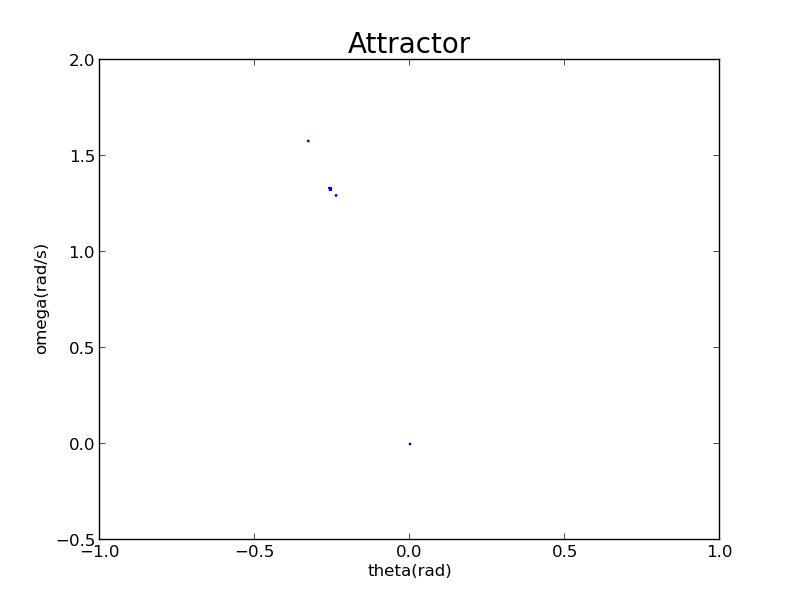
According to the bifurcation diagram,when $F_D=4$,it has only once period

Only one closed cycle is bold, which means it is repeated by many times.Other cycles are transient.
And its attractor has only a bold point (actually a lot of points) and other small points.

3

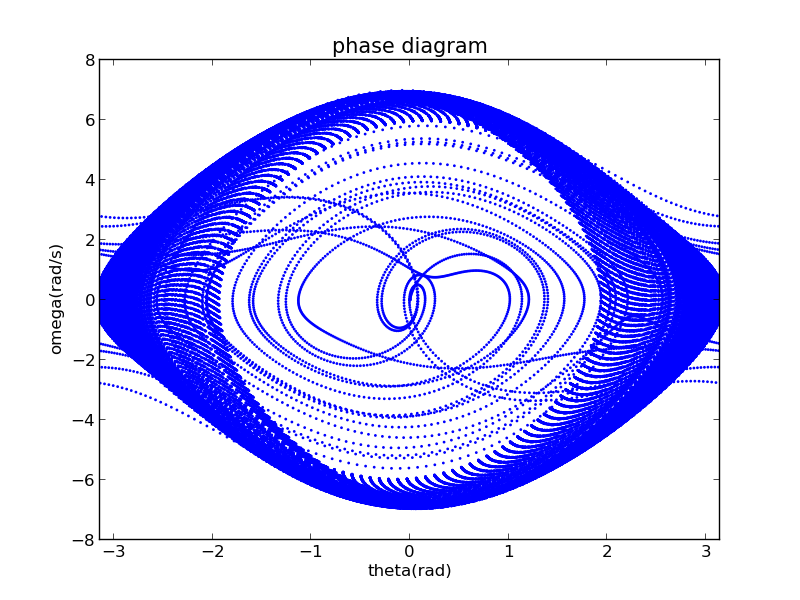
According to the bifurcation diagram,when $F_D=7.1$,the system is under the state of intermittency chaos. Its phase trajectory is also dense,but not full of the whole figure.

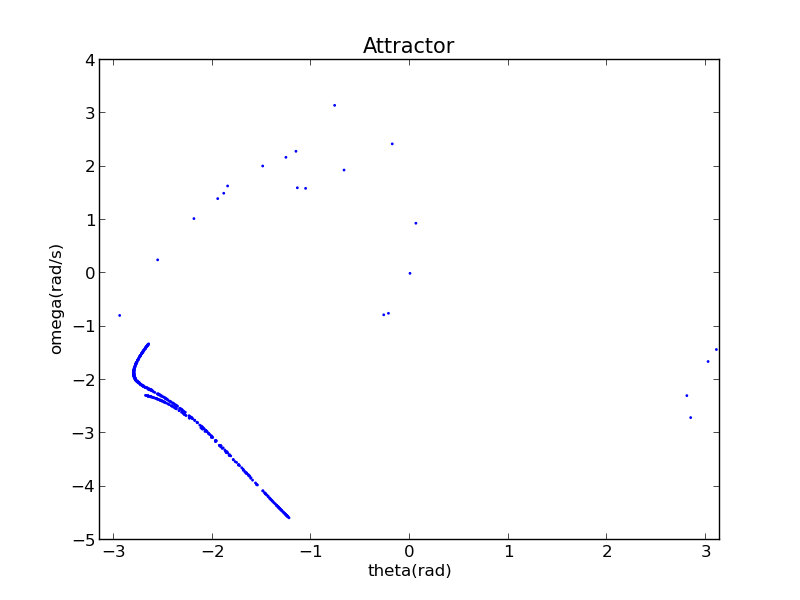
Its attractor includes a curve and other a few small points:

4

According to the bifurcation diagram,when $F_D=7.2$,it is not chaotic but periodic between two chaotic states.

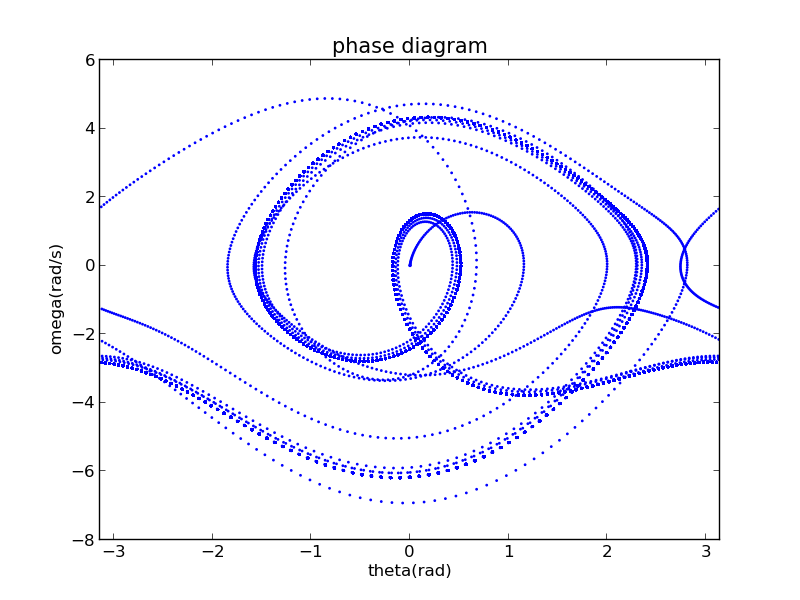
Its attractor is only a few points

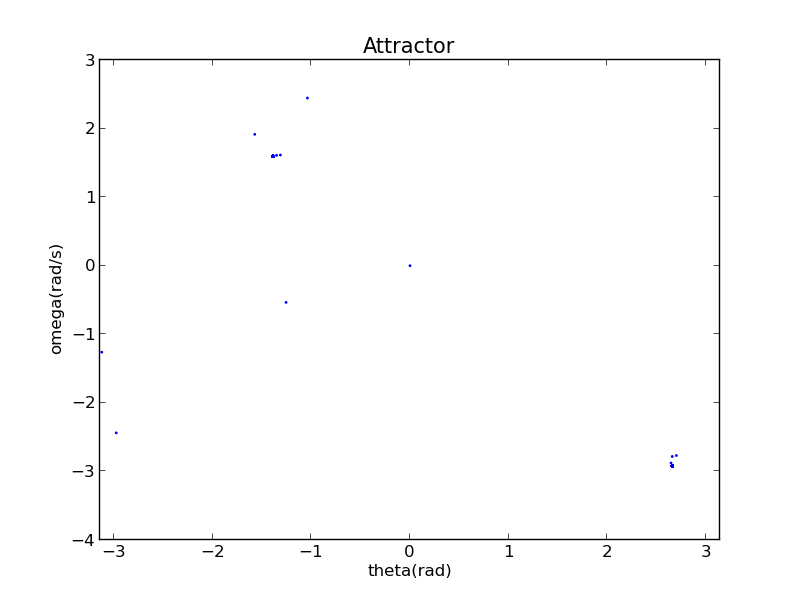
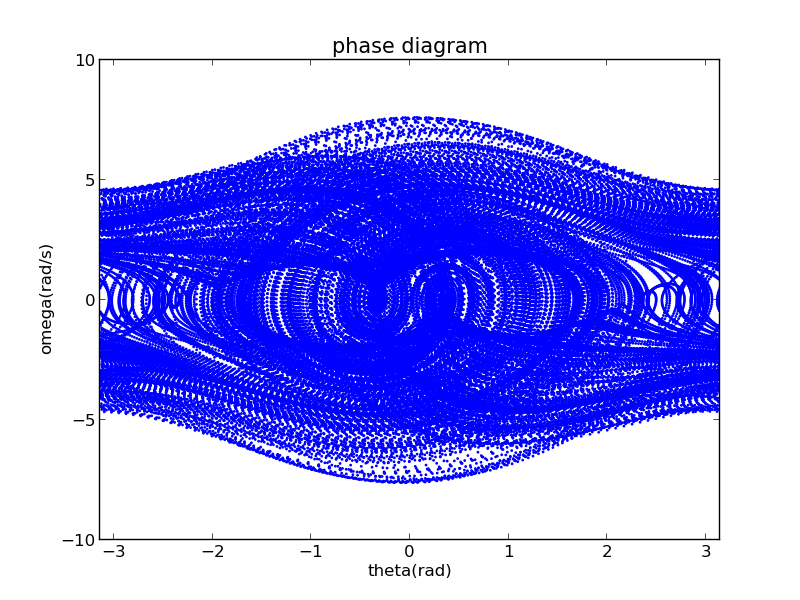
When $F_D$ has other values,its phase diagrams also can be seen from these links:phase diagram of $F_D=10$;phase diagram of $F_D=6.8$and so on.

Bifurcation Diagram of q

Modify anterior program,we can plot the bifurcation diagram of q.
For instance, fix $F_D=9$, change q from 0 to 2,
its bifurcation diagram is

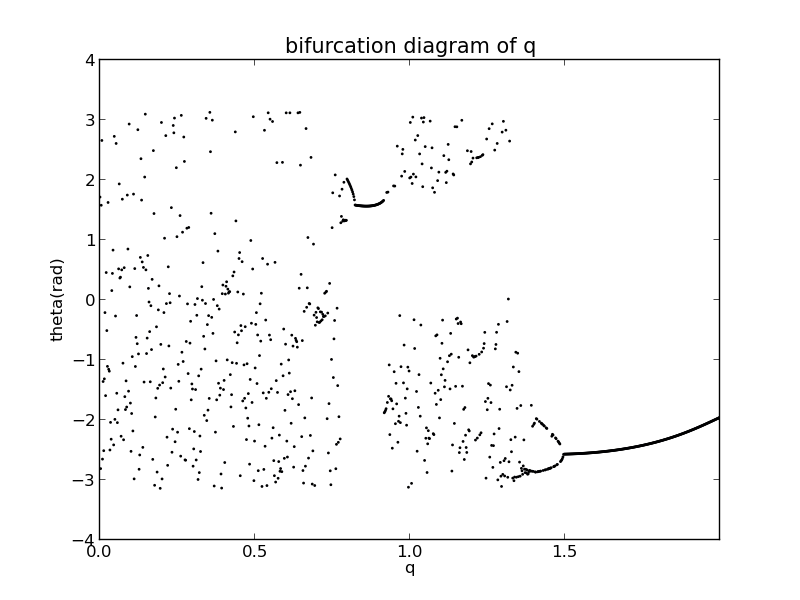
Another example:

Fix $F_D=7.1$, change q from 0 to 10,
its bifurcation diagram is

Magnity its horizontal axis between 0 and 2,

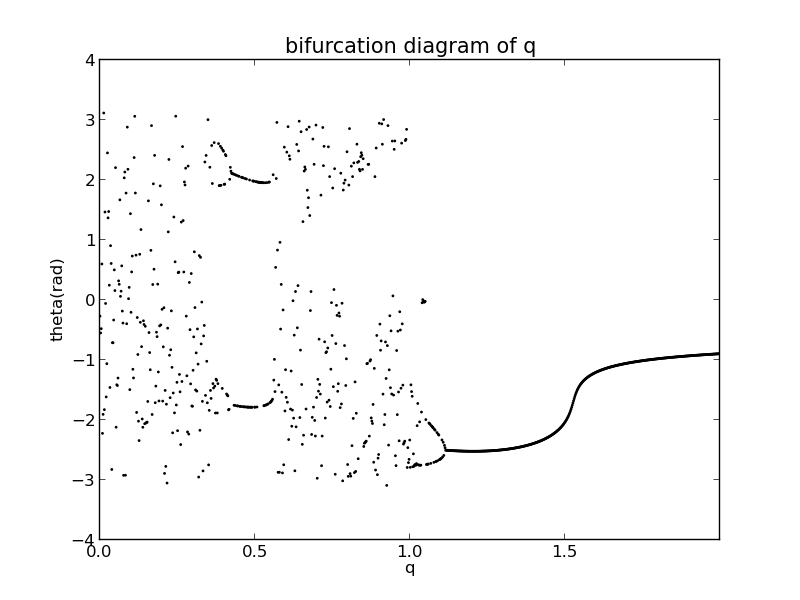
By the way, when $F_D=4$, its bifurcation is only a line without bifurcation.

Conclusions

• 1.Bifurcation diagram can be used to learn about the global chaotic properties of nonliear system.
• 2.Bifurcation diagram has fractal structrues,which is similar under different scales.
• 3.The phase trajectories of chaotic systems are all dense,quasiperiodic.
• 4.Attractors of chaotic states are some almost continuous curves,while attractors of periodic states consist of only several discrete points.
• 5.Generally speaking,chaos tends to happen when the amplitude of driven force is large and frictional coefficient is not too large.

Reference

[1]N.J. Giordano,H.Nakanishi.Computational physics(second edition).Tsinghua University Press.
[2]Z.Zhang.Chaos,fractal and soliton.Wuhan University Press.

Appendix

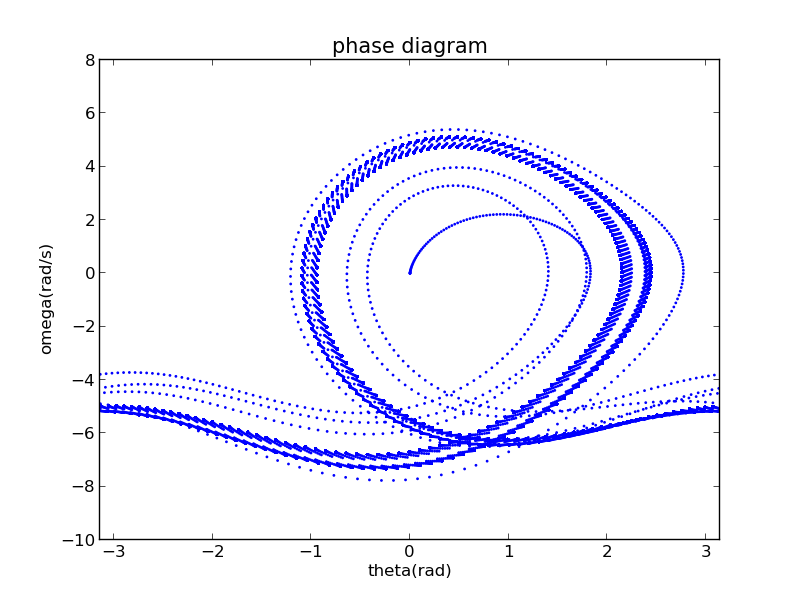
When $F_D=10$,$\omega_D=2$,$q=1$,let 'total time=2000 period of driven force' and 'dt=total time/30000',
the following strange pictures appeared:

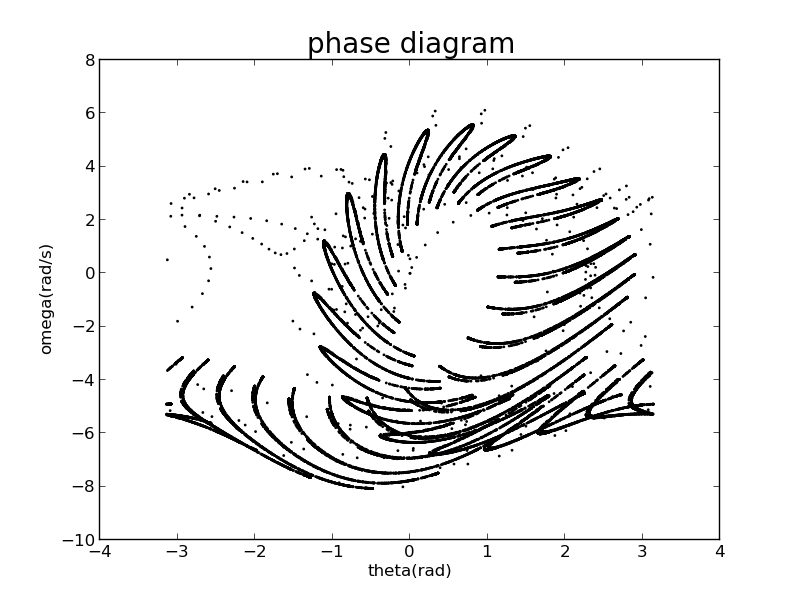
I can't explain it,I can't understand how it forms such figure!
Its normal phase diagram should be