Random System

Random

Abstract

The motion of a particle or molecule in solution can be analogous to a random walk.The article will consider serveral different types of random walks.

Random walk model

Being different from general dynamics systems, random walk model has no dynamics equation. Its motion mechanism can be described by following procedure:
Record the location of it as $x$, firstly, generate a random number $r$ between 0 and 1, then compare the number with another definite number $p_+$ which can determine the probability that it goes right, if $r>p_+$, update $x$ to $x+1$; otherwise to $x-1$.
Average $x^2$ is proportional to time $t$ or say step number $n$.
Because every step length is unity, we have the conclusion $<x^2_n>=n$.

Random walk in 1 dimension

Program code
Random.py
The step length is unity

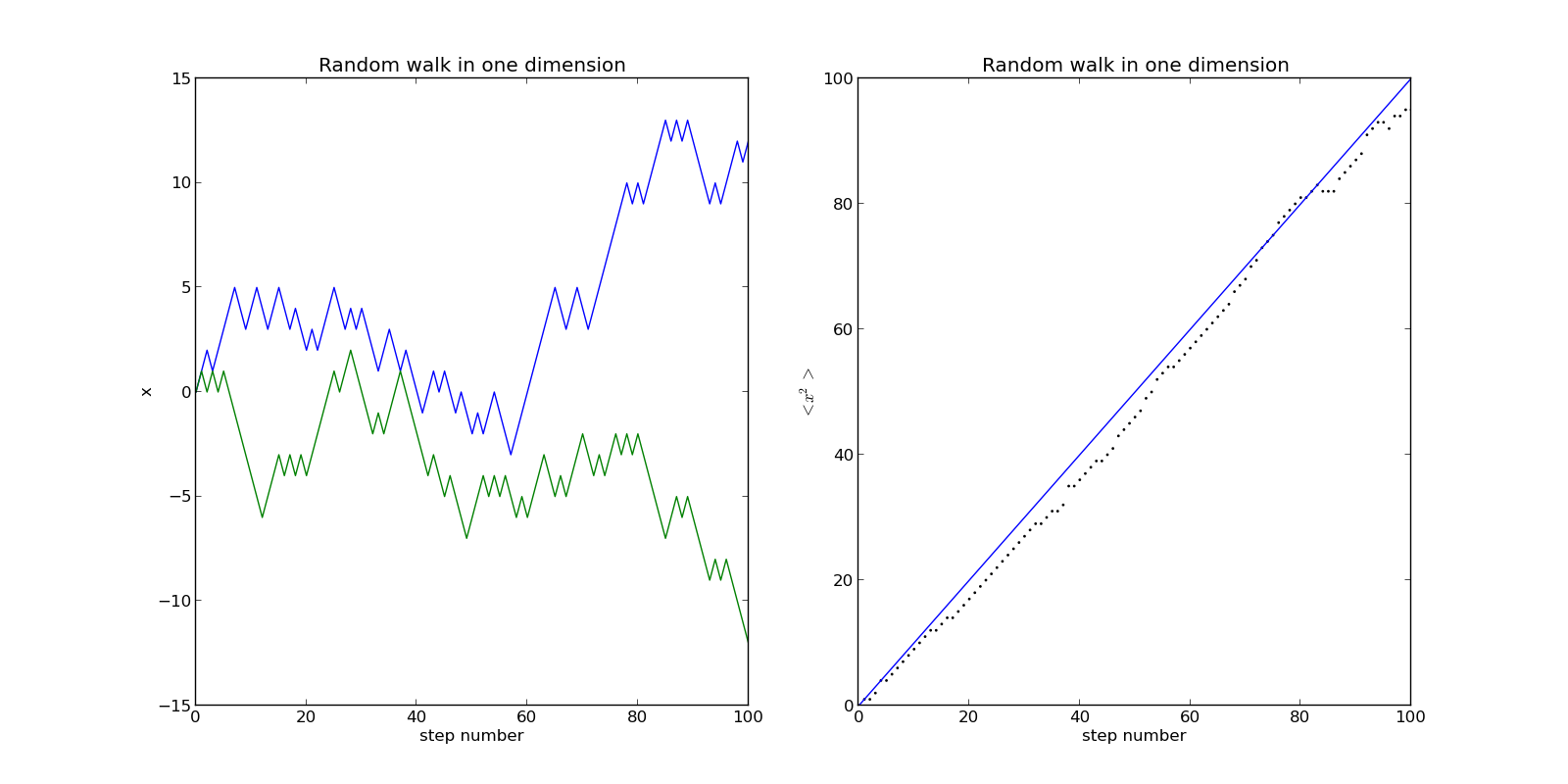
Left: $x$ versus step number, for 2 random walks in 1 dimension.
Right: $<x^2_n>$ as a function of step number (or t) for a collection of 501 random walks.The equation of the straight line is $y=x$(or $<x^2>=t$).
We can find that these points are all around the straight line, which demonstrates they have well proportional relationship $<x^2>=t$.

Problem 7.3

If $p_+=0.25$, let we see what will happen.

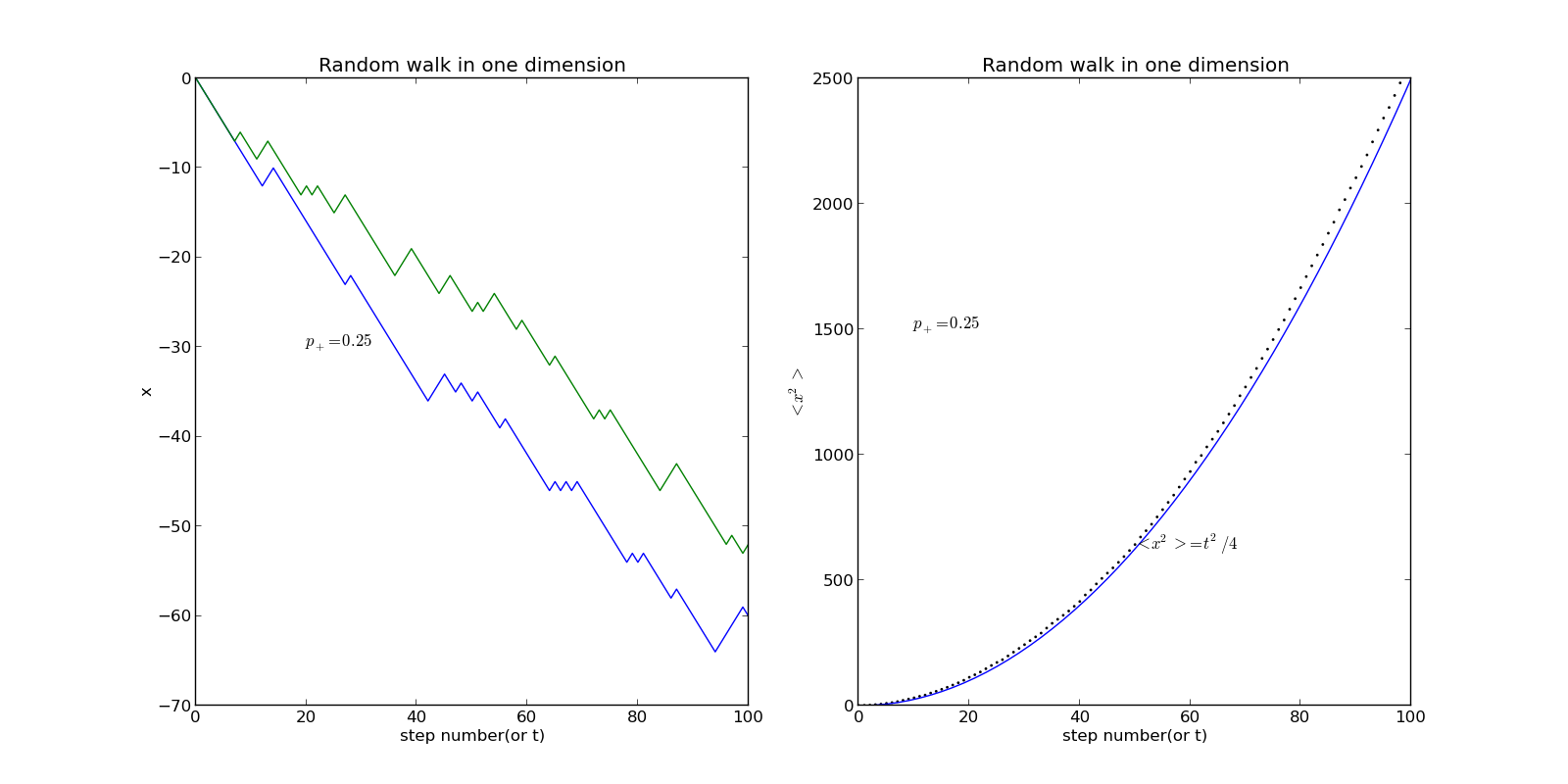
The equation of the curve in right figure is $y=x^2/4$ (or $<x^2>=t^2/4$), NOT a straight line.
It is obvious that the walker tends to go down.
$<x_n>=0.25n-0.75n=-n/2=t/2$
Thus $<x_n^2>=(-n/2)^2=n^2/4=t^2/4$

Random step length

More realistically, if we let $\Delta x=x_{i+1}-x_i$ become a random number between -1 and 1, or say it has random step lengths.

It seems to approach straight line $<x^2>=t/3$.
Average dispacement $<x>=0$, while average squared step length $\bar{L^2}=\int_{-1}^1 x^2f(x)dx=\int_{-1}^1 x^2\frac{1}{2}dx=\frac{1}{3}$
So $<x^2>=n\bar{L^2}=n/3=t/3$

program code
Ran.py

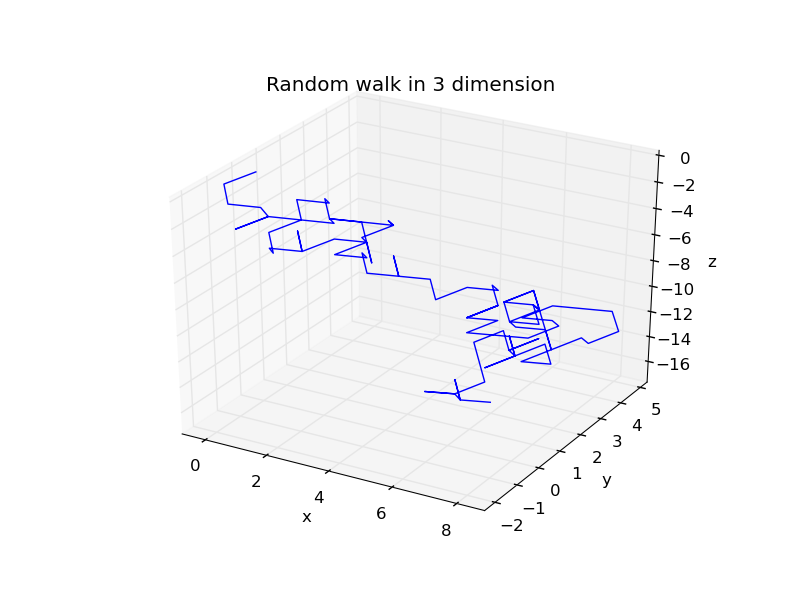
Random walk in 3 dimension

Random3D.py
This is trajectory of a random walk in 3 dimension.Walker started from the origin (0,0,0).

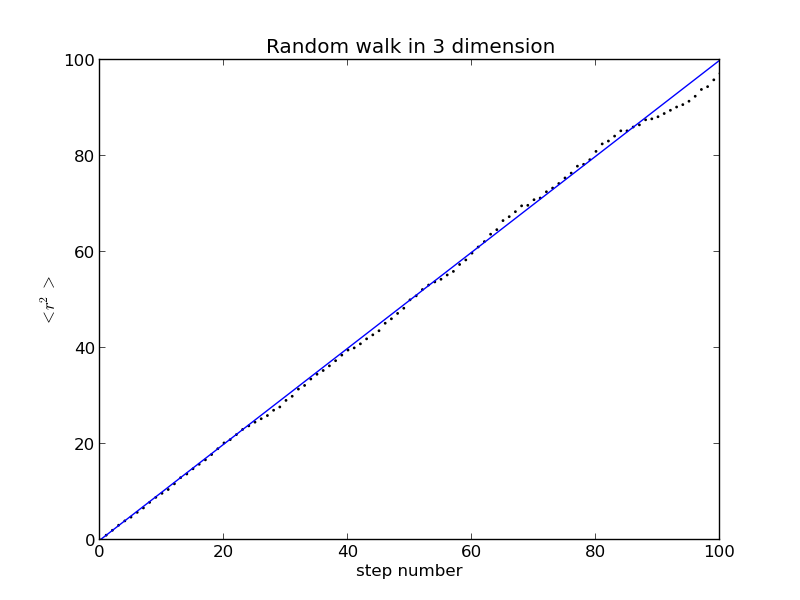
Let $r^2=x^2+y^2+z^2$, similarly, we have $<r^2_n>=n$.

Conclusions

-For 1 dimensional random walk, $<x^2>$ and step number $n$ or time $t$ have this relationship $<x^2_n>=n$
-When $p_+=0.25$, $<x^2>$ satisfies equation $<x^2>=t^2/4$, not straight line;
-For 3 dimensional random walk, similarly, we have $<r^2_n>=n$.