Exercise 06 Trajectory of A Backspined Fastball

（15级物院弘毅 陈亦林 2015301020152）

计算物理作业 Quastion2-19自旋球路径问题

---

【摘 要】 : 由书上内容可知，棒球在空中运动时会受到重力和空气阻力的作用在不考虑空气阻力，只考虑棒球受到重力影响，有初始自旋角速度情况下的运动，棒球还受到Magnus力，使得轨迹变得十分复杂。通过python模拟轨迹，解决题目2-19。
【关键词】: python, Magnus力, 自旋球, 轨迹

I. 问题回顾

Model the effect of backspin on the range of a batted ball. Assume an angular velocity of 2000rpm.

II. 理论推导

首先, 考虑没有空气阻力下棒球运动的Magnus力表达式为：

$$\vec{F}_{M}=S_0（\vec{\omega}×\vec{v}）$$
侧投球的曲线球的方程：
$$\frac{dx}{dt}=v_x, \frac{dv_x}{dt}=-\frac{B_2}{m}vv_x-wv_yS_0$$
$$\frac{dy}{dt}=v_y,\frac{dy}{dt}=-g-\frac{B_2}{m}vv_y+wv_xS_0$$
其中${B_2}$ 满足：
$$\frac{dx}{dt}=v_x, \frac{dv_x}{dt}=-\frac{B_2}{m}vv_x-wv_yS_0$$
代入空气阻力的表达式为：

$$\frac{B_2}{m}=0.0039+\frac{0.0058}{1+exp[(v-v_d)/\delta]}$$
（上式中，取$v_d=35$，$\delta=5 m/s$）

III. 自旋球在空中平抛运动的一般轨迹

为了能先得到较为清晰简洁的物理图像，我们首先以投掷初始速度v=31，初始投掷位置（0，0，1）的平抛抛掷曲线为例
棒球半径为0.1m并且角速度为2000rpm，沿着X轴正方向运动，初速度为31m/s。
运行代码，用matplotlib得到在三维情况下的运行轨迹如图,其中红色为 起始位置，黑色为最终位置
其轨迹图如下：

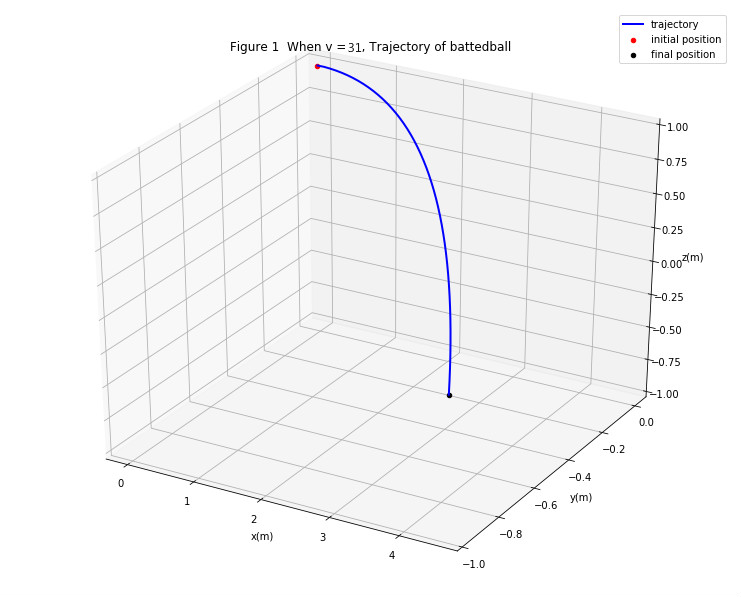
图1 源代码

我们得到了三维空间的自旋球在空中平抛运动的一般轨迹。
从图中可以看出，初始情况存在自旋时，轨迹相对没有自旋时有明显的偏移.

IV. 初始位置相同时，不同初始速度对自旋球在空中平抛运动的轨迹影响

进一步，我们探究投同初始位置相同时，不同初始速度对自旋球在空中平抛运动的轨迹影响。
保持棒球半径为0.1m，角速度为2000rpm，初始沿着X轴正方向运动，初始位置为（0，0，1）不变时，初始速度v=30,35,40,45,50,55m/s时的抛掷曲线。
其轨迹图如下：

图2 源代码

我们得到了三维空间的相同初始位置，不同初始速度时，自旋球在空中平抛运动的轨迹。
从图中可以看出，初始位置相同时，初始速度越大，自旋球在空中平抛运动的轨迹偏移量越大。

Ⅴ.初始速度相同时，不同初始位置对自旋球在空中平抛运动的轨迹影响

再进一步，我们探究初始速度相同时，不同初始位置对自旋球在空中平抛运动的轨迹影响。
保持棒球半径为0.1m，角速度为2000rpm，初始沿着X轴正方向运动，投掷初始速度v=31m/s不变时，初始投掷位置分别为（0，0，1），（0，0，2），（0，0，3），（0，0，4），（0，0，5），（0，0，6）时的抛掷曲线。
其轨迹图如下：

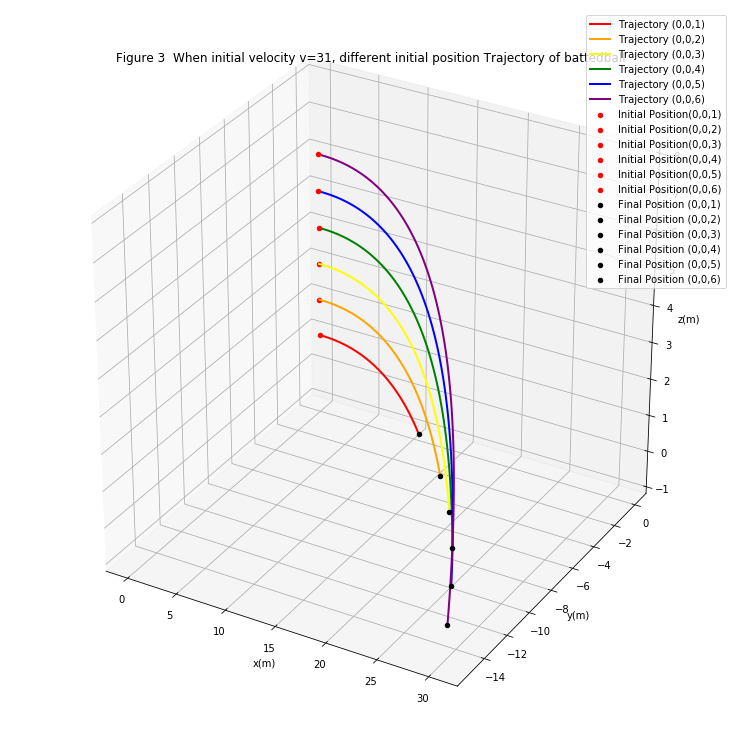
图3 源代码

我们得到了三维空间的相同初始速度，不同初始位置时，自旋球在空中平抛运动的轨迹。
从图中可以看出，初始速度相同时，初始位置越高，自旋球在空中平抛运动的轨迹偏移量越大。

VI. 结论

本次作业主要讨论了棒球的运动问题，模拟了棒球在忽略空气阻力情况下Magnus力对棒球运动的影响，发现棒球初始时自旋对棒球轨迹也有很大影响，棒球旋转方向不同，其偏移也会发生变化。
同时经过探究得知：初始位置相同时，初始速度越大，自旋球在空中平抛运动的轨迹偏移量越大。初始位置相同时，初始速度越大，自旋球在空中平抛运动的轨迹偏移量越大。因此通过控制自旋方向和出手时的自旋速度可以在一定程度上控制棒球运动轨迹。