Exercise 07 Pendulum

（15级物院弘毅 陈亦林 2015301020152）

计算物理作业 Quastion3-11有驱动阻尼摆问题

---

【摘 要】 : 由书上内容可知，对于摆的运动，在考虑了摩擦并加入了强制驱动力等因素后，体系便形成了一个混沌系统。任何轻微的改变都会造成不可预知的影响，使得轨迹变得十分复杂。本次作业使用改进后的Euler-Cromer方法进行计算，并且通过python模拟轨迹，解决题目3-11。
【关键词】: python, 非线性钟摆模型, 摩擦, 驱动

I. 问题回顾

For the three values of $F_{D}$ shown in Figure 3.6, compute and plot the total energy of the system as a function of the time and discuss the results.

II. 理论推导

在考虑了摩擦、重力、驱动力后，摆的受力方程为：

$$\frac{d^2θ}{dt^2}=-\frac{g}{l}sinθ-q\frac{dθ}{dt}+F_Dsin(Ω_Dt)$$

$$\frac{d\omega}{dt}=-\frac{g}{l}sinθ-q\omega+F_Dsin(Ω_Dt)$$

（上式中，取$\frac{g}{l}=1$，q=0.5，$Ω_D=2/3$）

III. 在不同$F_D$情况下，摆的摆动角度随时间的变化关系

1.当$F_D=0$时

以初始运动方向为正向，摆偏离竖直线角度随时间变化如下图：

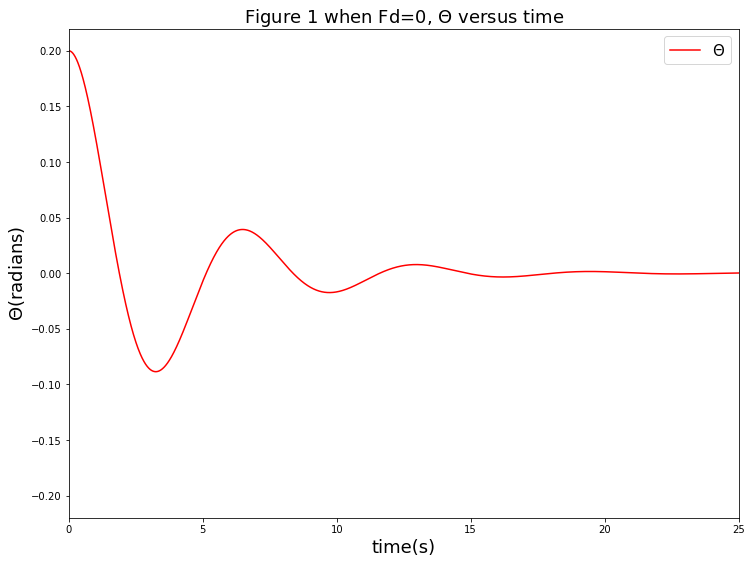
从图中可以看出，在没有驱动力的条件下，摆受摩擦力的影响，其摆角逐渐衰减，最终在20秒左右完全停下.

2.当$F_D=0.5$时

以初始运动方向为正向，摆偏离竖直线角度随时间变化如下图：

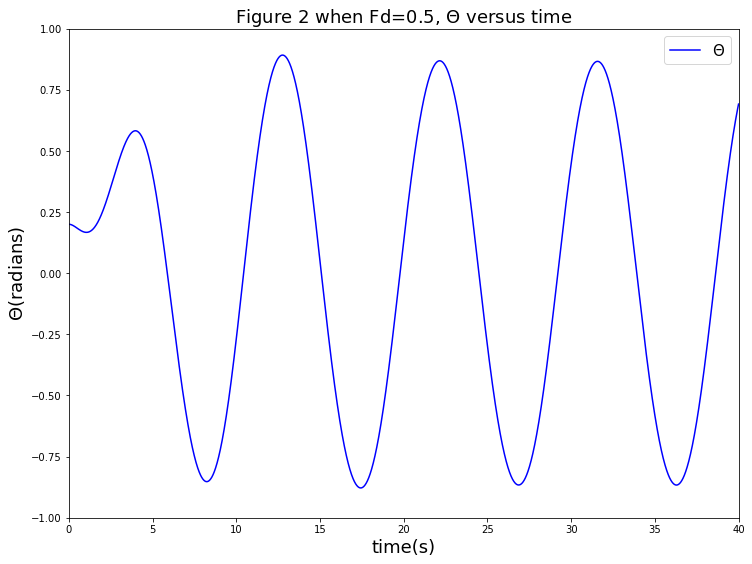
从图中可以看出，在有驱动力，但其大小适宜的条件下，摆同时受摩擦力的影响，其摆角逐渐趋于稳定，发生共振.

3.当$F_D=1.2$时

以初始运动方向为正向，摆偏离竖直线角度随时间变化如下图：

从图中可以看出，在有驱动力，但其过大的条件下，摆同时受摩擦力的影响，其摆角一开始是混沌状态，没有确切的规律，但最后在长时间后趋于稳定.

IV. 在不同$F_D$情况下，摆的总能量，动能，势能随时间的变化关系

进一步，我们探究在不同$F_D$情况下，摆的总能量，动能，势能随时间的变化关系。

1.当$F_D=0$时

首先，考察摆的总能量随时间的变化关系。其曲线如下图：

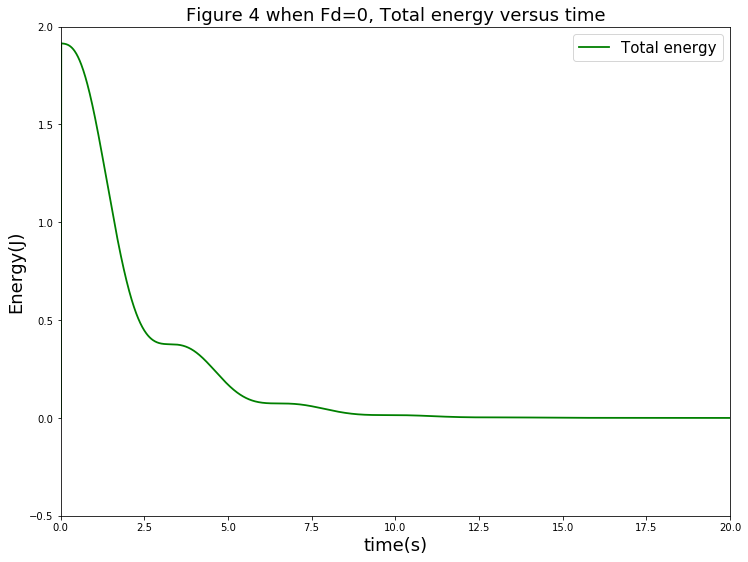
从图中可以看出，在没有驱动力的条件下，摆受摩擦力的影响，其总能量逐渐衰减，最终在20秒左右完全耗散.
其次，考察摆的动能随时间的变化关系。其曲线如下图：

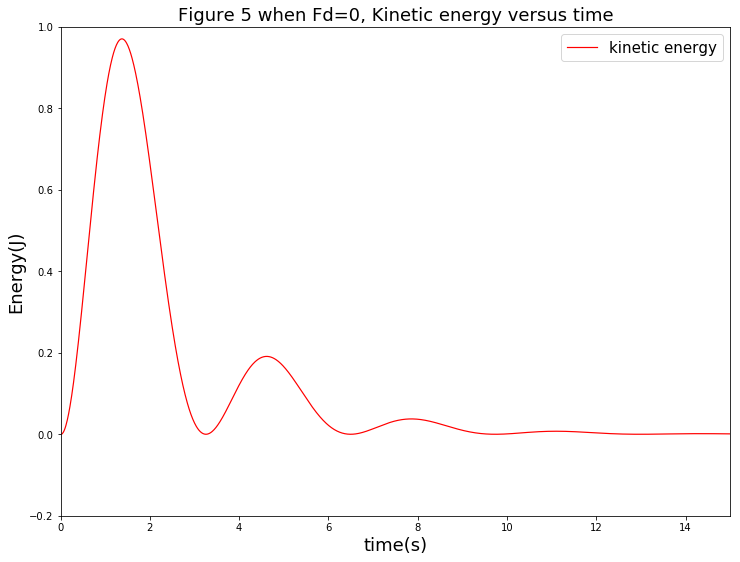
从图中可以看出，其动能现进行了一小段时间的振荡，但是其幅度逐渐衰减，最终在14秒左右完全耗散.
接着，考察摆的势能随时间的变化关系。其曲线如下图：

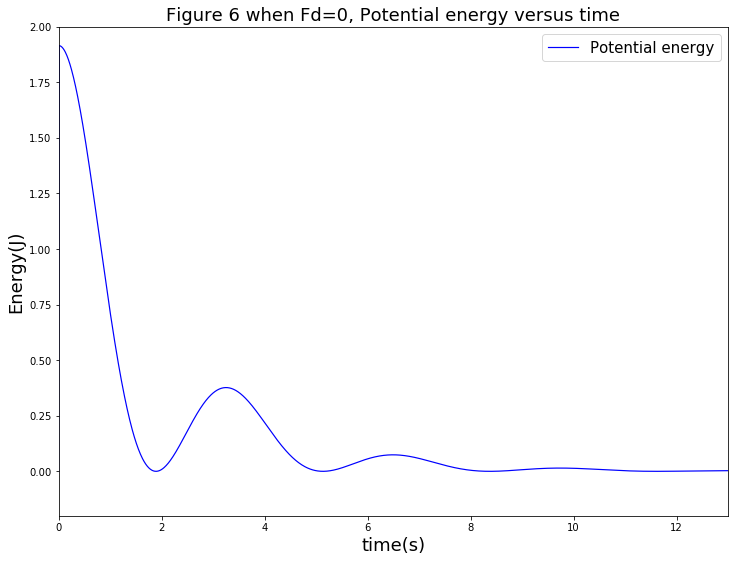
从图中可以看出，其势能逐渐衰减，最终在12秒左右完全耗散.
最后，为了得到一个更清晰地物理图像，我们把三项综合在一张图上，方便观察和比对，如下图：

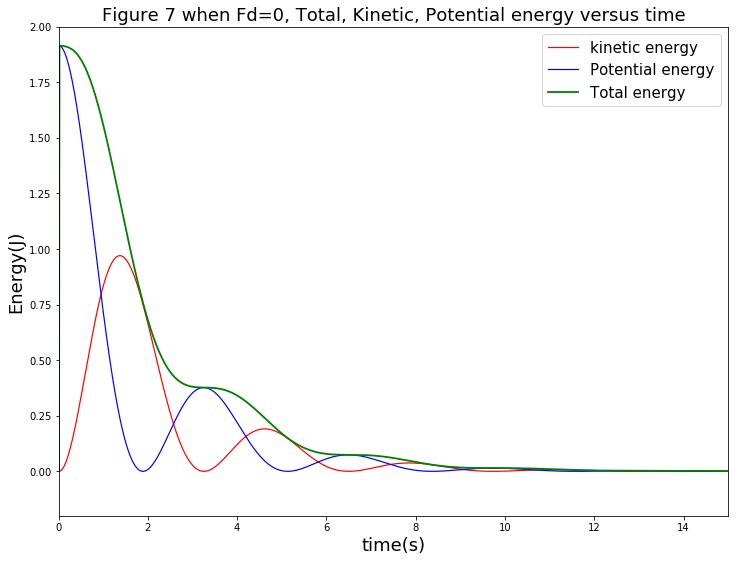
该过程中，图中也可看出能量守恒的体现。

2.当$F_D=0.5$时

同理，先考察摆的总能量随时间的变化关系。其曲线如下图：

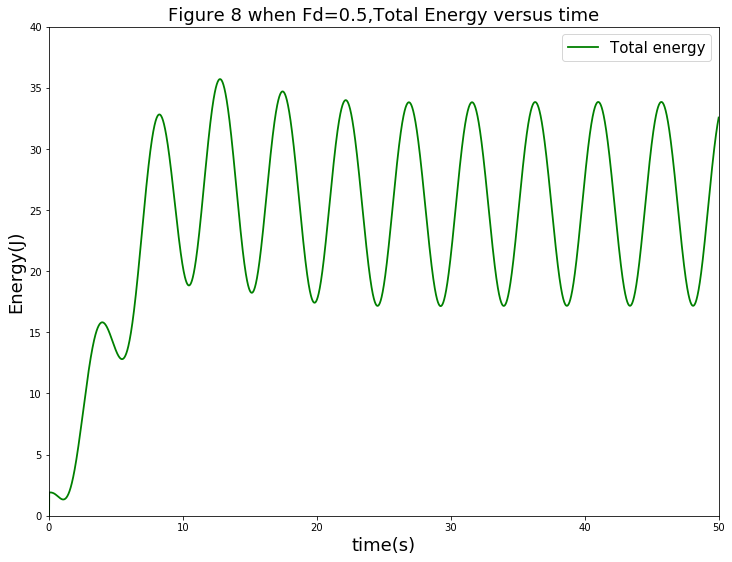
从图中可以看出，在有驱动力，但其大小适宜的条件下，摆受摩擦力的影响，其总能量先升高，并且最终达到一个稳定的振荡状态。
其次，考察摆的动能随时间的变化关系。其曲线如下图：

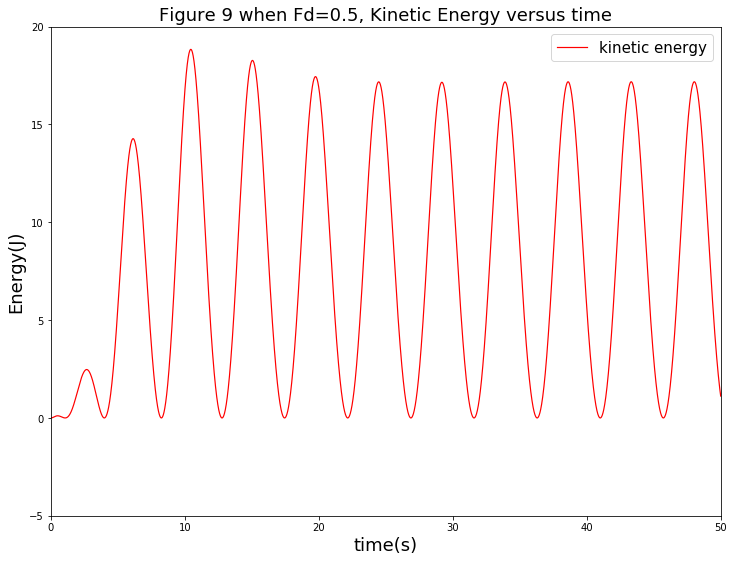
从图中可以看出，其动能先升高，并且最终达到一个稳定的振荡状态。
接着，考察摆的势能随时间的变化关系。其曲线如下图：

从图中可以看出，其势能先升高，并且最终达到一个稳定的振荡状态。
最后，我们把三项综合在一张图上，如下图：

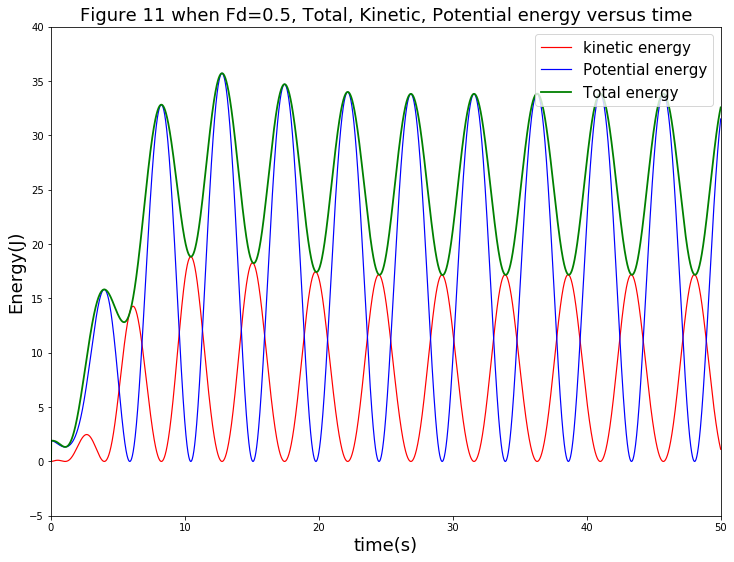
同理，该过程中，图中也可看出能量守恒的体现。

3.当$F_D=1.2$时

同理，先考察摆的总能量随时间的变化关系。其曲线如下图：

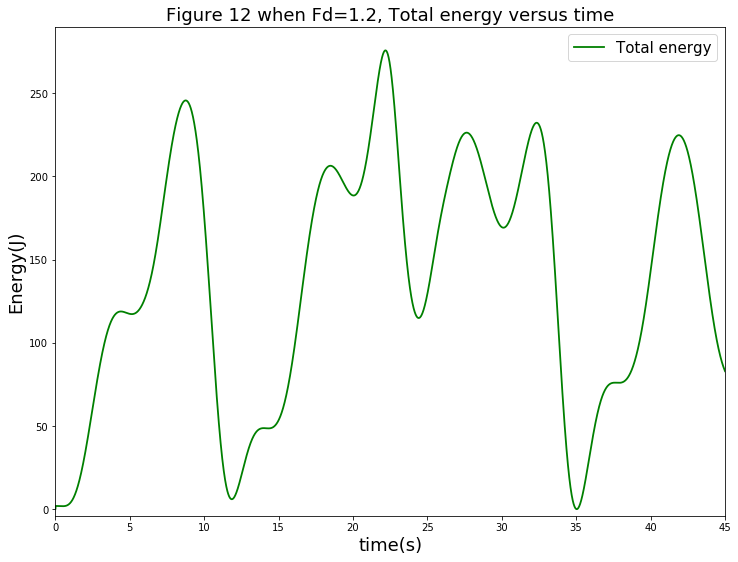
从图中可以看出，在有驱动力，但其过大的条件下，摆同时受摩擦力的影响，其总能量变得不可预测具体规律，陷入混沌。
其次，考察摆的动能随时间的变化关系。其曲线如下图：

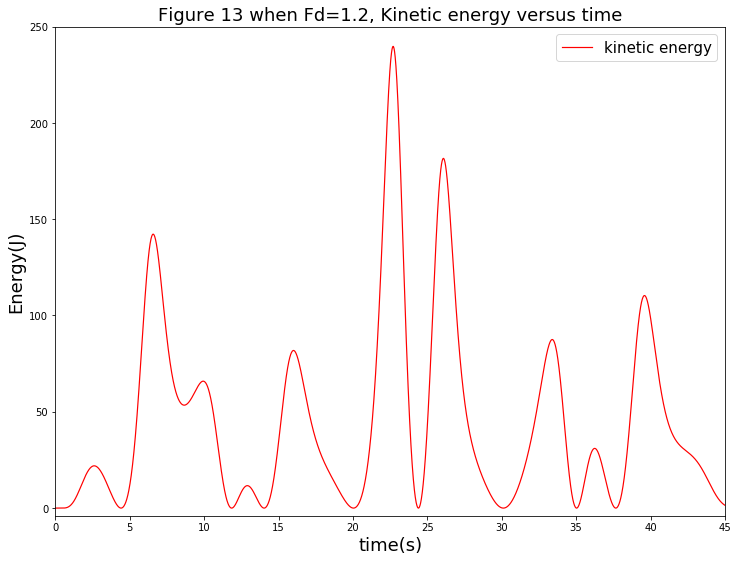
从图中可以看出，其动能同样变得不可预测具体规律，陷入混沌。
接着，考察摆的势能随时间的变化关系。其曲线如下图：

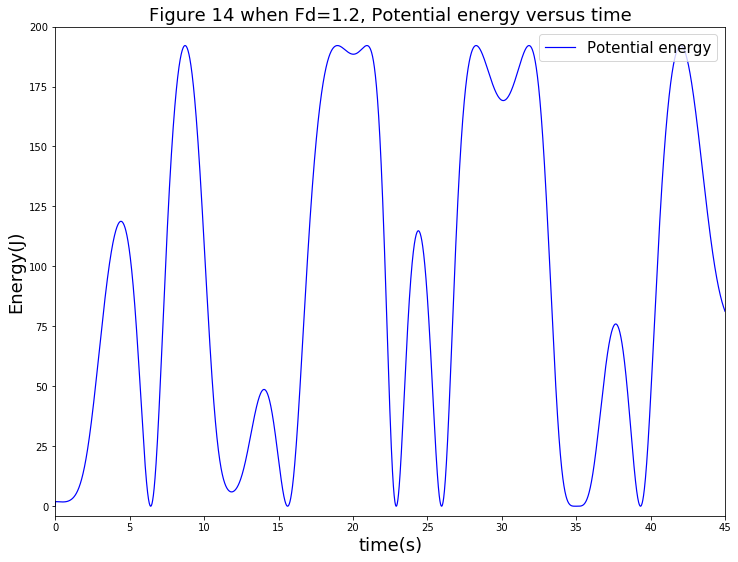
从图中可以看出，其势能同样变得不可预测具体规律，陷入混沌。
最后，我们把三项综合在一张图上，如下图：

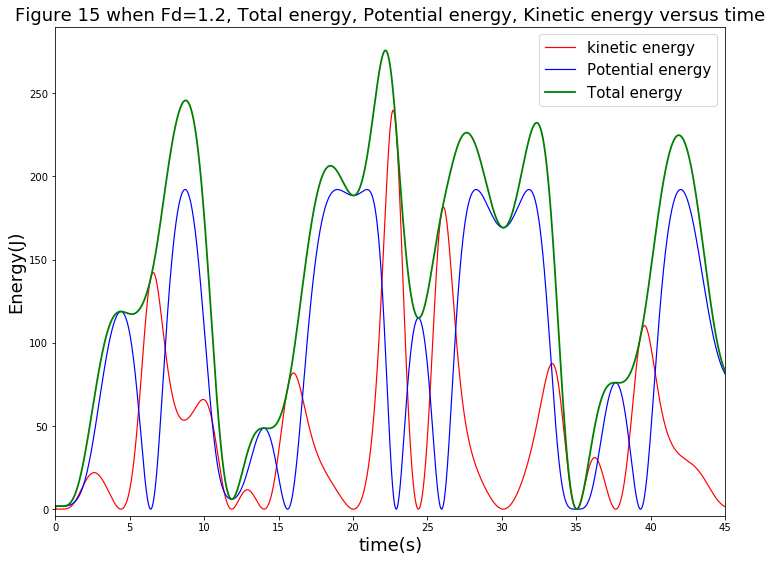
同理，该过程中，图中也可看出能量守恒的体现。

源代码（由于本次作业所有图和计算只需要在该代码上改变Fd的参数，以及对最后输出曲线进行选择哪种曲线输出，所以基本都是完全一样的，这里就是源代码基础）

VI. 结论

本次作业主要讨论了有驱动力和摩擦的摆的运动问题，探究了非线性钟摆模型。
得出驱动力在较小，以及适宜的情况下，都不会出现非线性的混动情况，都是可预测的。可是当驱动力过大时，发生混沌现象，其运动变得不可预测。因为任何一点微小的改变都会带来巨大的差异和影响。

VII . 鸣谢

感谢黄梓宸同学在编程方面的指导！