@Homework-
2016-06-11T12:55:09.000000Z
字数 1111
阅读 453
第四章作业(第一次)
未分类
摘要:
本次完成作业题目chapter4_problem4.7,双星系统在不同质量比的情况下运动轨道的变化。以及非平方反比情形下运动轨迹。
背景介绍:
在地日轨道中,一般认为太阳的质量足够大,往往忽略太阳的运动,但当行星质量不远小于中心天体质量时,中心天体不再能够近似为相对体系质心静止的状态。
利用牛顿第二定律,以及在太阳系中,行星受到太阳的引力作用:
可知:
即行星运动规律。
采用天文学单位,利用Euler-Cromer method:
正文:
Binary
Binary
为了获得简明的双轨道,任意时刻保持系统动量:()
选取初始位置pos_1 =(1.,0.,0.], pos_2 = (-1.,0.,0.),
当双星质量:=1:0.4时:
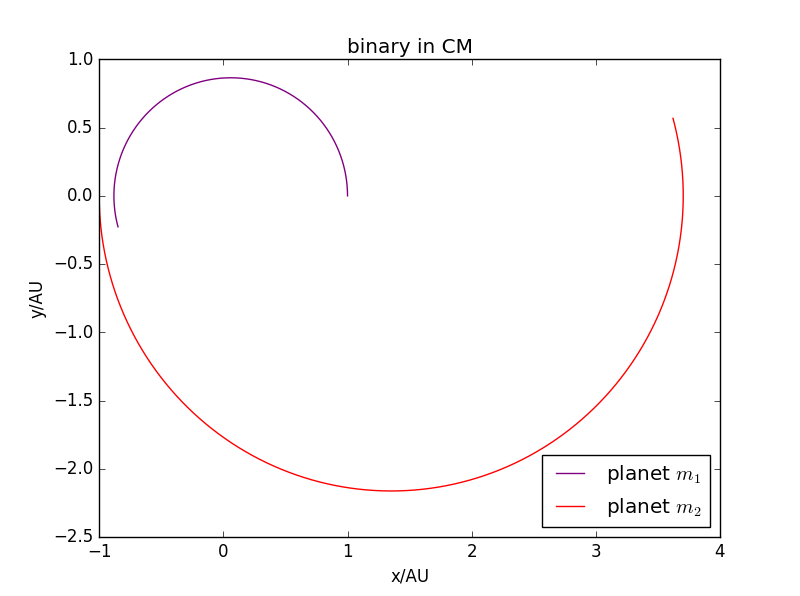
不闭合
当双星质量:=1:0.6时:
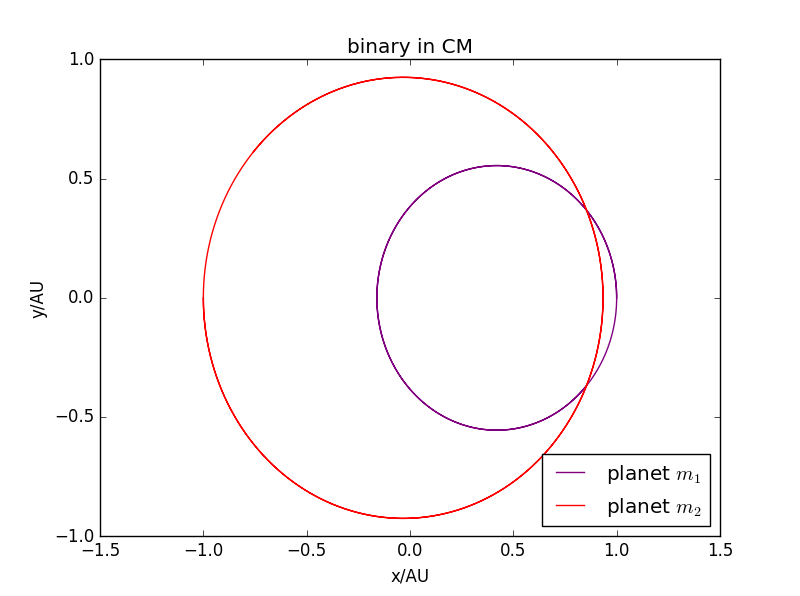
闭合椭圆
当双星质量:=2:1时:
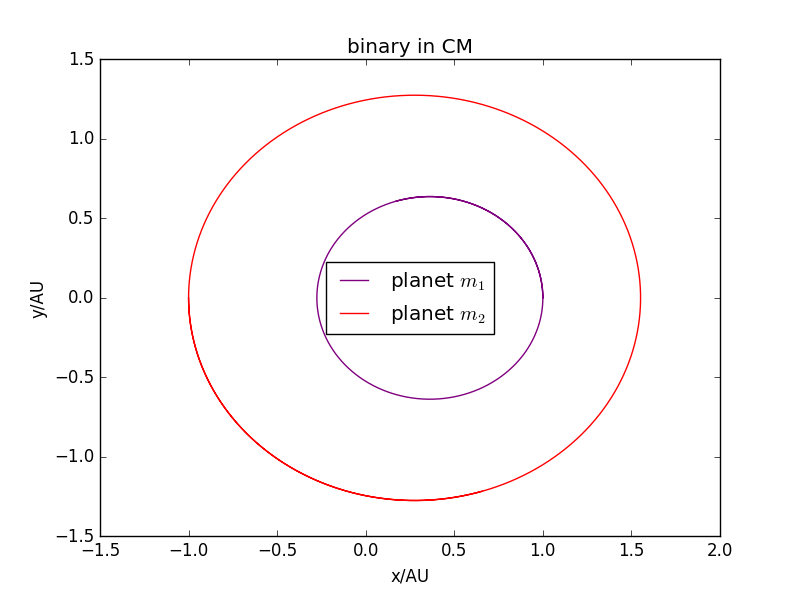
当双星质量:=1:1时:
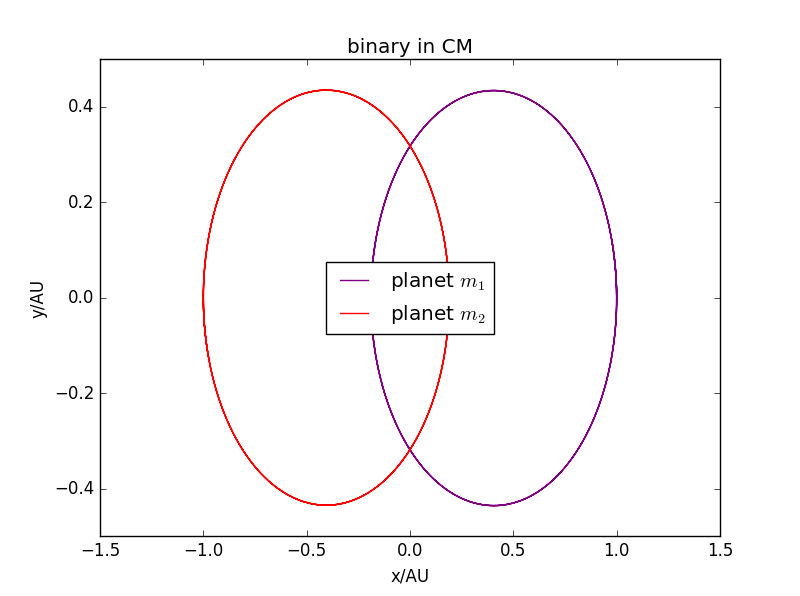
做相同轨迹运动,初始条件影响位置。
当:=1:30时:
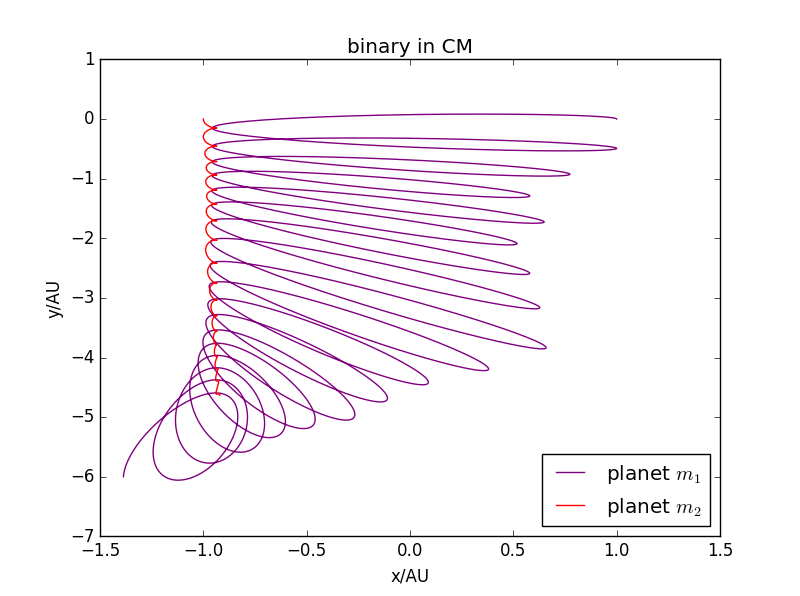
显然质量远大于时:
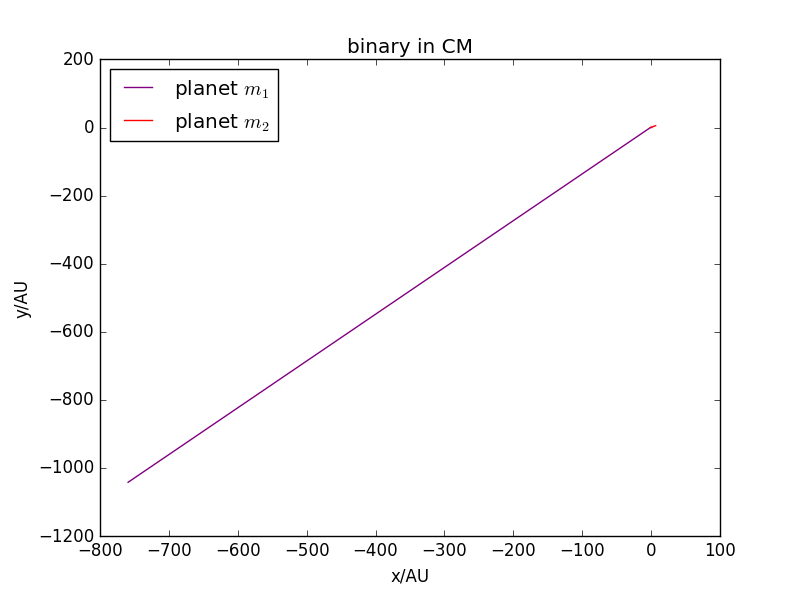
由于保持系统动量为0,此时较大。
静止时:
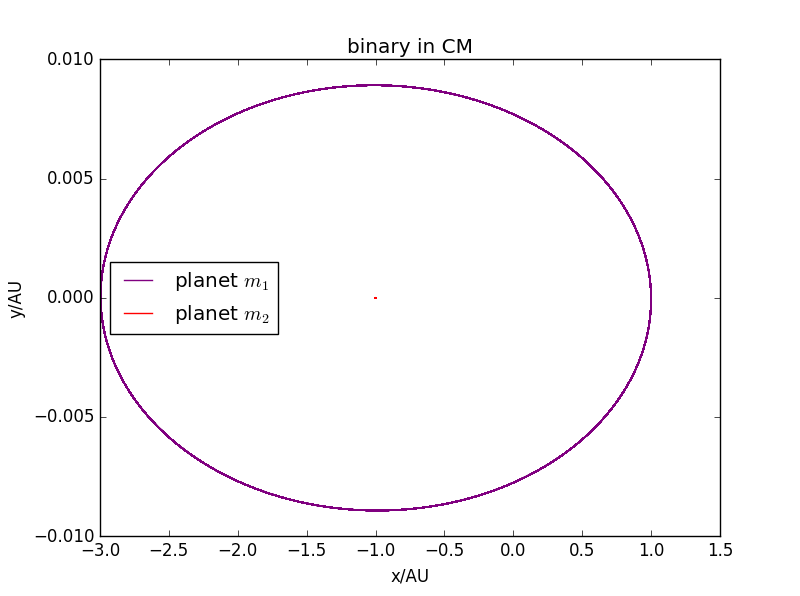
:> 1:0.45时:
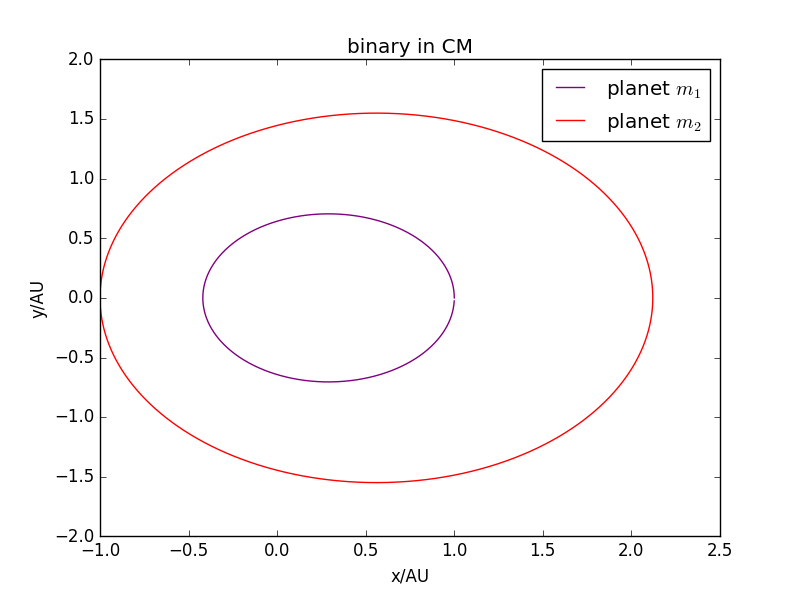
: < 1:4时:
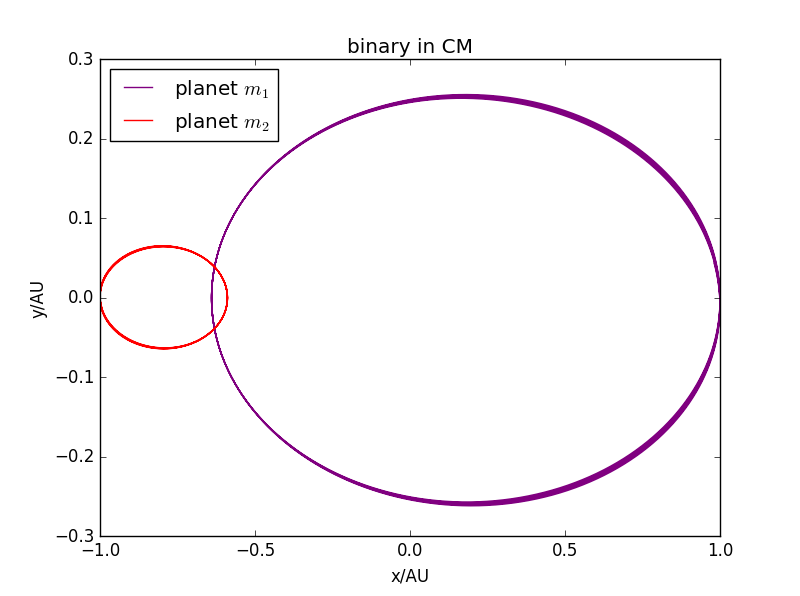
轨道闭合。
非平方反比:代码
当不满足平方反比时,可以发现,轨道不稳定。\

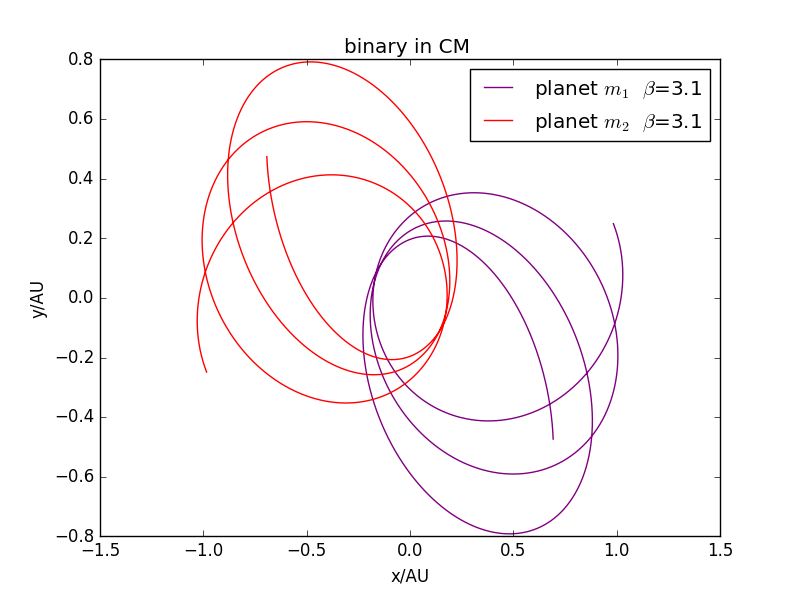
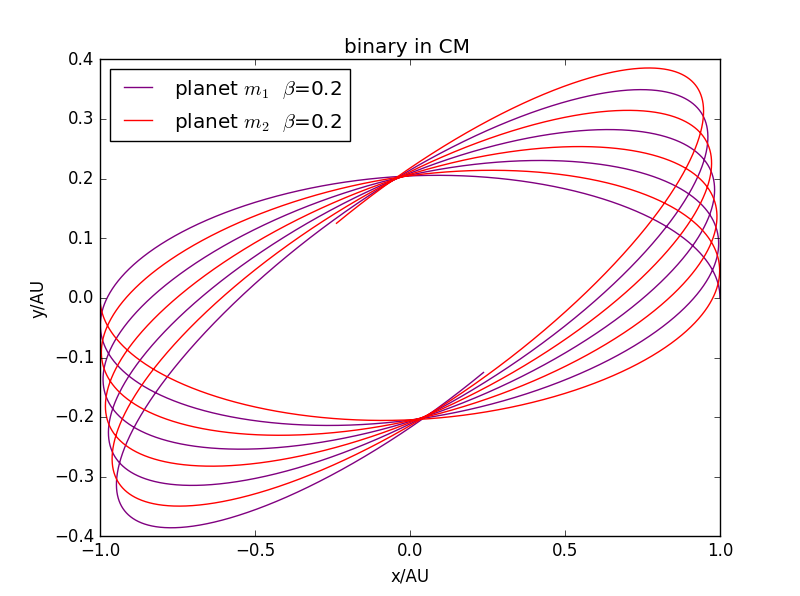
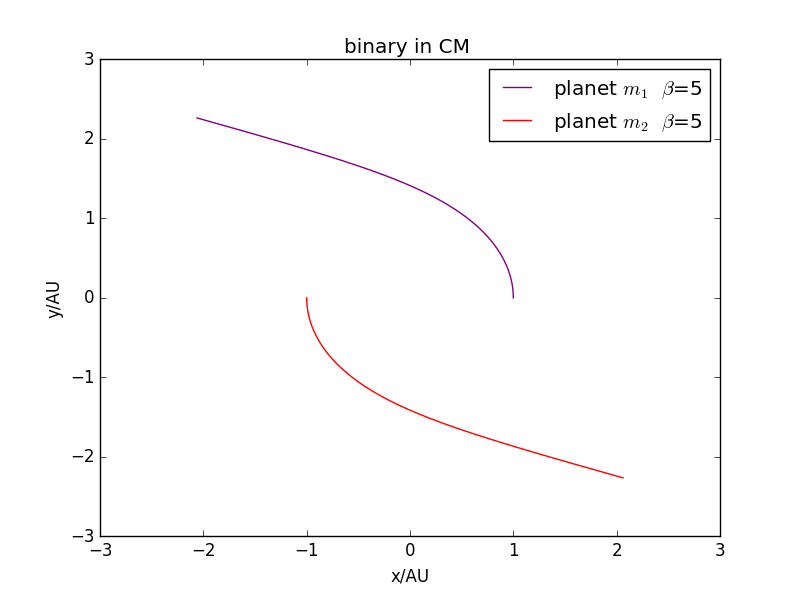
结论:
1.条件合适时,双星轨道为圆形。
2.当质量比在1:0.45---1:4之间时,x-y具有闭合轨道。
3.当不满足平方反比时,可以发现,轨道不稳定
致谢:
[1]N.J. Giordano,H. Nakanishi.Computational Physics(second edition)(影印版).清华大学出版社
