@shaobaobaoer
2018-05-28T00:38:43.000000Z
字数 2383
阅读 1528
快速排序
0x00 题目描述
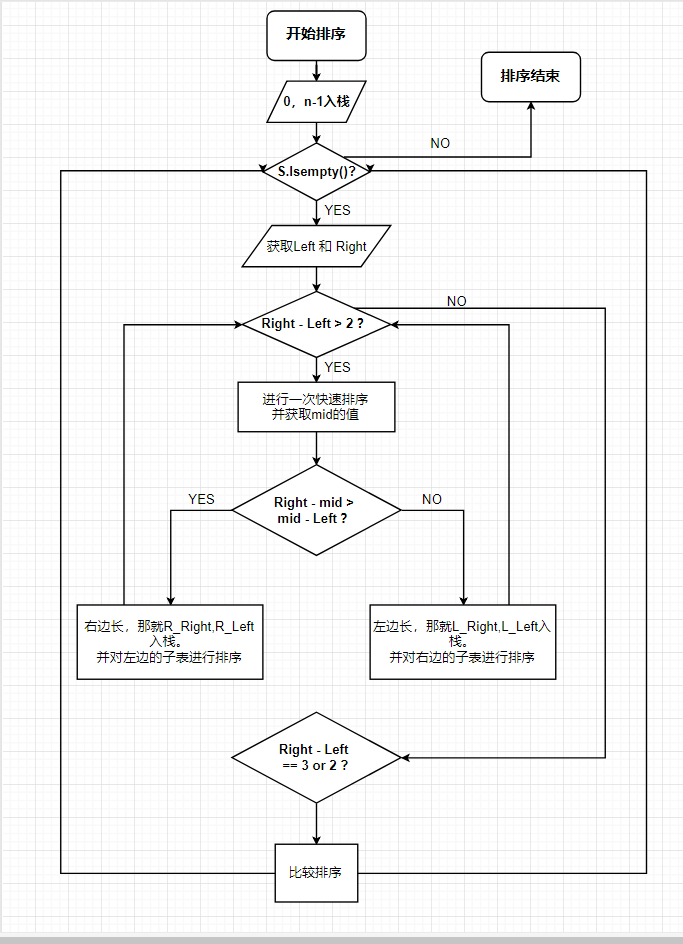
按照下述原则编写快速排序非递归算法:
- 一趟排序后,若子表已经有序(无交换)则不参加排序,否则先对长度较短的子表进行排序,将另一个子表的上下界入栈保存
- 若待排序元素数≤3,则不再进行分割,而是直接进行比较排序。
0x01 实现原理
(以流程图或盒图等形式画出)
快速排序由C. A. R. Hoare在1962年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
至于快速排序算法,会在后面有详细的解释。这边给出的是题目的构造
0x02 实现技术
(可说明如何使用或改进完善教材程序)
快速排序算法介绍
备注: 我这里的快速排序算法和教材上给出的不太一样。该算法来自于 数据结构考研笔记 殷人昆著 。
虽然实现方法不一样,但是基本思想还是一样的。并且按照这个方法完成了作业。
传入参数Right ,Left 。表示需要排序的数组的一部分 (如果要对数组a下标从i到j的部分排序,那就传入的参数为Right=j,Left=i。
并将基准数记为 a[Left]
比如说传入的数组为a[10]={6 1 2 7 8 3 4 5 10 9}
| a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| value | 6 | 1 | 2 | 7 | 8 | 3 | 4 | 5 | 10 | 9 |
对上述数组进行快读排序,传入的参数为Right=j,Left=0
此时 i=0;j=9
| a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| value | 6 | 1 | 2 | 7 | 8 | 3 | 4 | 5 | 10 | 9 |
| I/J | i | j |
哨兵 j 先从左边开始移动,移动到一个比基准数小的位置。这里 j 会移动到 7 的位置。之后开始移动 i 。从右边开始移动,移动到一个比基准数大的位置。第一次移动后结果如下:
| a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| value | 6 | 1 | 2 | 7 | 8 | 3 | 4 | 5 | 10 | 9 |
| I/J | i | j |
然后交换i和j的位置。并再一次进行如上的排序,直到i和j相遇
- 第二次i j 内推。 i 停在了 8 的地方,j 停在了 4 的地方。
| a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| value | 6 | 1 | 2 | 5 | 8 | 3 | 4 | 7 | 10 | 9 |
| I/J | i | j |
- 第三次i j 内推。 i j 在 3 的地方。交换该位置与基准数。本次排序结束。
| a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| value | 6 | 1 | 2 | 5 | 8 | 3 | 4 | 7 | 10 | 9 |
| I/J | i j |
总结来说就是这样:
/* 0 1 2 3 4 5 6 7 8 9* 6 1 2 7 8 3 4 5 10 9* 3 1 2 5 4 6 8 7 10 9* L M R* 较长的序列在前面的情况,长序列上下界入栈,* 下次会对长的序列排序*/
- 之后,得到两个部分,一个是 a[0..4] 与 a[6..9]的部分。再次进行递归。直到i和j相等。
快速排序非递归算法介绍
任何递归算法都可以通过栈来实现。这点毋庸置疑。快速排序算法也可以用非递归算法实现。所需要用到的数据模型是 栈 。
大体的伪代码如下:
int QK_sort_NonRecursion(int Array[]) {LinkStack<int> s;s.Push(0); s.Push(n - 1); //注意压栈顺序,这里先压入的是0<Left>后压入的 n-1<Right>while (!s.IsEmpty()) {s.Pop(Right);s.Pop(Left);//注意出栈顺序while (Right - Left > 2) {///当子序列长度大于三的时候,那就没有排序完毕mid = QK_sort_Partition(Array, Left , Right ); //先将表进行一次排序///按照题目要求,先对长度短的子表进行排序,并将另一子表的上下界入栈保存if (Right - mid > mid - Left) {//右边长,那就R_Right,R_Left入栈。并对左边的子表进行排序} else {//左边长,那就L_Right,L_Left入栈。并对右边的子表进行排序}if (Right - Left == 2) 比较排序if (Right - Left == 3) 比较排序}}
这点和教材上的代码较为类似。
0x03 文件结构说明
(说明工程所含有的所有源代码文件和支持文件(如输入输出的文本文件)及其功能)
| 文件名 | 文件类型 | 功能简介 | 备注 |
|---|---|---|---|
| Node.h | head file | 节点类 | 来自 沈俊老师的代码 |
| LinkStack.h | head file | 栈类 | 来自 沈俊老师的代码 |
| Assistance.h | head file | 辅助程序 | 来自 沈俊老师的代码 |
| main.cpp | cpp file | 主程序 | QK_sort_Recursion 快速排序递归算法 QK_sort_Partition 完成一趟快速排序的过程 QK_sort_NonRecursion 快速排序非递归算法 |
| CMakeLists.txt | CMAKE file | CMAKE | Clion 辅助文件 |
| cmake-build-debug | Document | 编译程序的文件夹 | Clion 生成的编译程序 |
0x04 实测试数据和输出结果
(要求几组具有代表性的数据,要求附如下所示的运行效果图, 或是实际运行的输入输出文件)
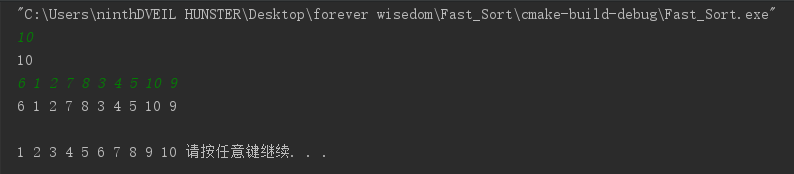
- 测试数据 1
- 例题中的 6 1 2 7 8 3 4 5 10 9
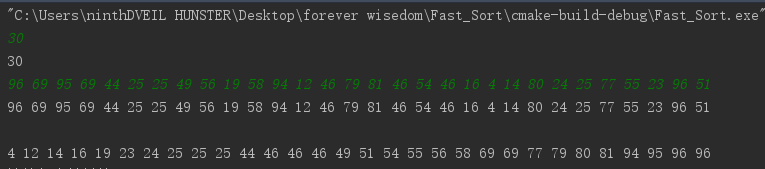
- 测试数据 2
- 1-100 中 的 30 个随机数
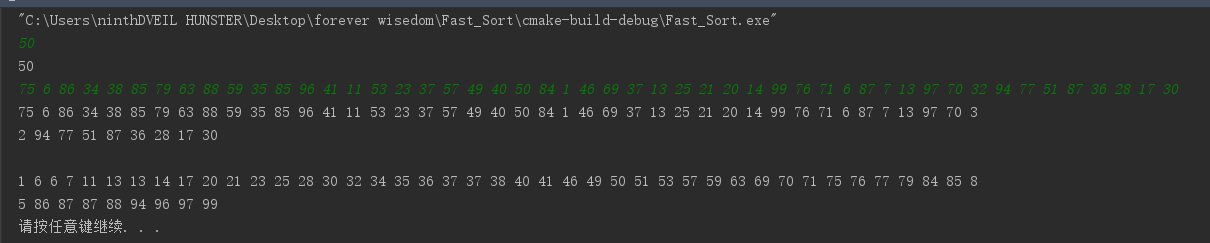
- 测试数据 3
- 1-100 中 的 50 个随机数
- 测试数据 4
- -100-100 中 的 20 个随机数
- 测试数据 5
- -100-100 中 的 41 个随机数

0x05 个人体会
5.(包括题目的难易、调试过程等)
5.1 题目评价
我觉得这道题目出题的角度很新颖。从某种程度上来说,这种结合比较排序算法的快速排序。从某种程度上比原本的快速排序算法更加优秀一些。
总之,觉得这道题目挺不错的。让我对快速排序算法有了新的理解和认识。
5.2 做题过程与感受
另外,教材中学习到的算法和我以前看到的快速排序算法有些不太一样。但是整体的思路还是一样的。我把教材中的代码仔细看了看,发现确实教材代码和我的代码有些不太一样,具体表现在 I 和 J 的位置调度上。最终两者的结果是一样的。(一开始看到我第一次排序和参考代码对比不一样的时候有点愣住,才发现自己掌握的快排和老师的有点不太一样)
总之,条条大路通罗马,尽管方法不一样,但是思路正确,最终自己经过调试DEBUG后还是能够实现的。
