@shaobaobaoer
2019-03-17T07:22:10.000000Z
字数 12753
阅读 1827
数据结构复习笔记(二)
数据结构 SHU
作者 0 ShaoBaoBaoEr
个人网站 shaobaobaoer.cn
QQ 2454225341
参考书目:# 数据结构高分笔记# 数据结构————C++s实现⌈ ⌉ 上取整⌊ ⌋ 下取整
0x02 森林与并查集
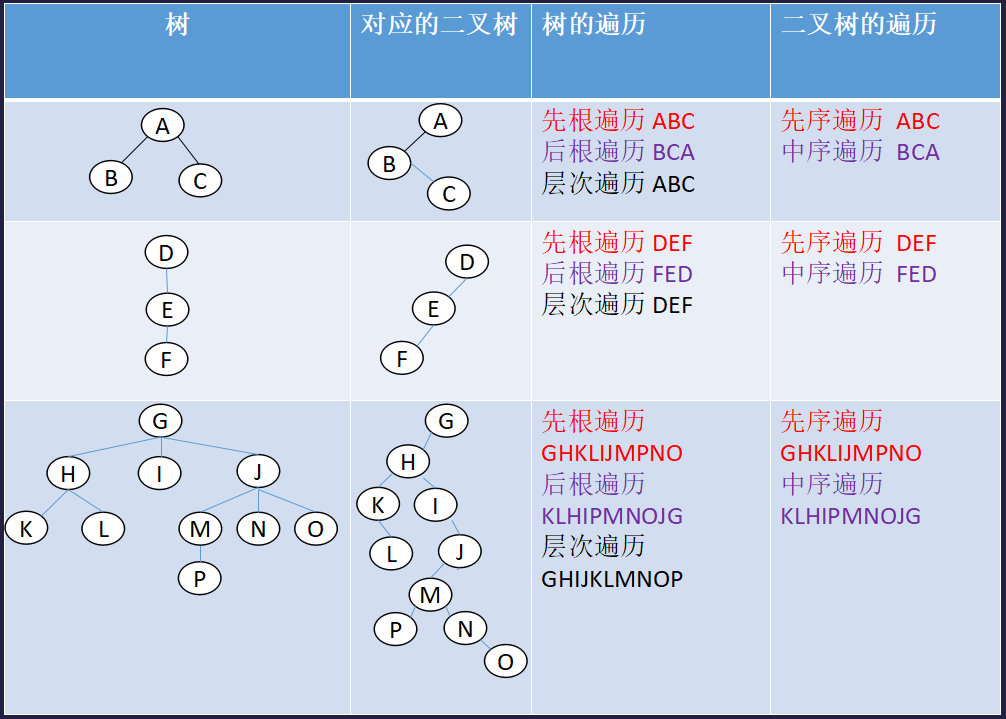
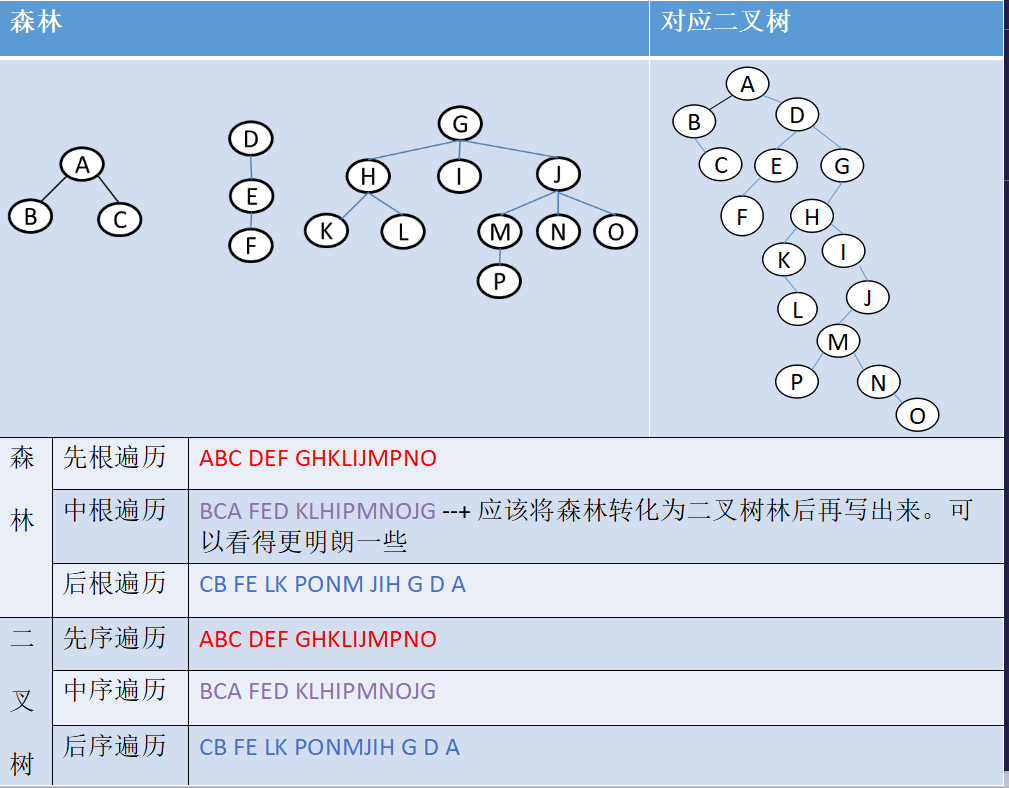
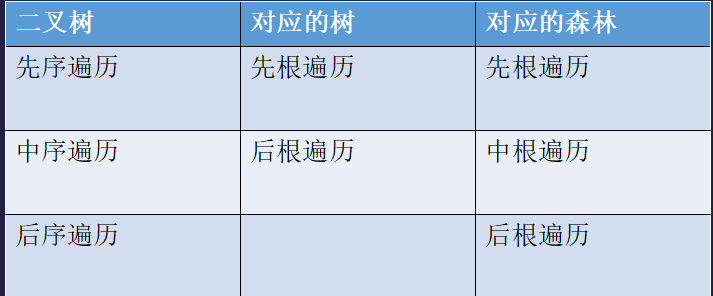
关于树,森林,二叉树的一些结论
把研讨的表格贴上来了。
0x01 图论
1. 概念梳理
图的存储结构
pass
DFS与BFS
- DFS 类似于二叉树的先序遍历。遍历一个点v后选择一个未被访问的点w,依次进行下去之后,再退回。
- BFS 类似于二叉树的层序遍历。遍历一个点v后选择所有与它临接的点访问,之后再访问它邻接点的所有点。
普利姆算法
关键思想:
从图中任意取出一个顶点,把它当成一棵树。从这棵树相接的边中选取一个权值最小的边,把这个边与连着的点加入树中。
- 建立数组 vset[] && lowcost[]
- vset[i]=0 表示顶点i没有并入树中
- lowcos存放当前生成树剩余各顶点最短边的权值。
- 选择v0,到其他边的边为候选边
- 重复以下步骤n-1次
- 从侯选边中跳出权值最小的边,将与其相连的v并入树中,更新vset[]
- 考察所有点,更新lowcost
算法分析:
- 复杂度
- 与图中顶点有关,与边无关。适用于稠密图
克鲁斯卡尔算法
关键思想:
每次找出侯选边中权值最小的边,将该边并入树中。重复直到所有边检测完。
- 将权值从大到小排列
- 从最小边开始扫描当前便会为侯选边(是否会形成回路),如果是,则加入。
算法分析:
- 可以很快将两个有很多元素的集合合并为一个(找到一棵树的树根并加入另一颗树中)
- 可以方便判断两个元素是否为一个集合。(如果有相同的根,那就是一个集合的)
- 复杂度 由边数e决定,适用于稀疏图
克鲁斯卡尔和普利姆都适用于无向图
迪杰斯特拉算法
关键思想:
设有有两个顶点集合S&T,S存放图中已经找到的最短路径的顶点
- T存放图中剩余的顶点。
- S只包含原点
- 不断从集合T中选取到顶点路径长度最短的顶点并入中。
集合S每并入一个新的顶点,都要修改顶点到集合T中顶点的最短路径长度
不断重复直到T的顶点都并入S
这看上去有点难。
实现步骤:
- 设置初始数组dist,path,set
- dist初始化,0对应0,0连出去的边设置为它的权值,无法连接到的边设置为
- path初始化,0对应-1,0连出去的边设置为0,其余设置为-1
- set初始化,0对应1表示已经妥当。
- 之后开始重复下列过程知道set全部为1
- 从dist中选择一个最小的权值,记其下标为j。然后把它连出去。并修改对应set的值。
- 对dist数组进行遍历。更新dist与path的值。伪代码如下
GET jfor i in range(len(dist)):if dist[i] > dist[j] + g[j][i]:path[i] = jdist[i] = dist[i] + g[i][j]
核心代码就是如此,这边附上完整的py代码。
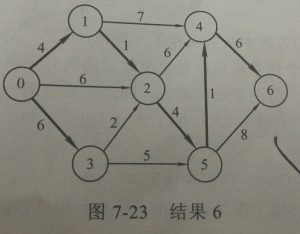
NaN = 0xFFFFdef Dist(G):''':param G: 邻接矩阵:return:dist & path'''dist = []path = []set = []for i in range(len(G)):path.append(-1)set.append(0)dist.append(NaN)set[0] = 1for i in range(len(G)):if G[0][i] == NaN:passelse:path[i] = 0dist[i] = G[0][i]i = 0while (i < len(G)):min = NaNfor j in range(0, len(G)):if set[j] == 0 and dist[j] < min:u = jmin = dist[j]set[u] = 1for j in range(0, len(G)):if dist[j] > dist[u] + G[u][j] and set[j] == 0:path[j] = udist[j] = dist[u] + G[u][j]i += 1return dist,pathif __name__ == '__main__':Graph = [# 0 1 2 3 4 5 6[NaN, 4, 6, 6, NaN, NaN, NaN],[NaN, NaN, 1, NaN, 7, NaN, NaN],[NaN, NaN, NaN, NaN, 6, 4, NaN],[NaN, NaN, 2, NaN, NaN, 5, NaN],[NaN, NaN, NaN, NaN, NaN,NaN, 6],[NaN, NaN, NaN, NaN, 1, NaN, 8],[NaN, NaN, NaN, NaN, NaN, NaN, NaN]]print(Graph[0][0] == NaN)Dist(Graph)
返回的数组为
dist = [0, 4, 5, 6, 10, 9, 16]# dist 放得是0的点到其余顶点最短路径的长度path = [-1, 0, 1, 0, 5, 2, 4]# path 放得是0的点到其余各顶点的最短路径# 比如 6 。其路径为 4 , 4需要通过 5到达,5需要通过2到达,2需要通过1到达,1需要通过0到达# 综上就是 0 -> 1 -> 2 -> 5 -> 4 -> 6
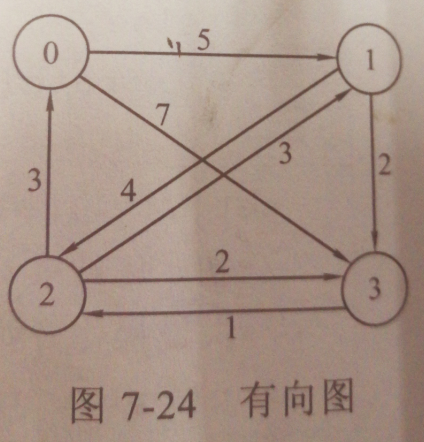
附上该题目的图片:
性能分析:
- 某一顶点到其余各顶点的最短路径
- 复杂度
弗洛伊德算法
如果求途中任意一对顶点间的最短路径,那就要用弗洛伊德算法
弗洛伊算法很麻烦,但是程序却很简单。主要思想就是
监测 k = ,如果 A[i][j] > A[i][] + A[][j] 则将A[][j] 改为这个值,并将PATH[i][j] 置为
实现步骤
- 设置矩阵A和Path,A为传入的邻接矩阵。Path全-1且与A的阶数相同。
- 监测 k = ,如果 A[i][j] > A[i][] + A[][j] 则将A[][j] 改为这个值,并将PATH[i][j] 置为
程序代码
这个我们还做了研讨来着。弗洛伊德算法的python程序如下:
class MGragph:def __init__(self, edges):self.edge = edgesself.n = len(edges)self.e = 0def __str__(self):return str(self.edge)def fuluoyide(self):Path = full((self.n, self.n), -1)# print(Path)A = self.edgeprint("A = \n", mat(A))print("PATH = \n", Path)for k in range(0, self.n):print("##################")print("目前监测 k = %s,如果 A[i][j] > A[i][%s] + A[%s][j] 则将A[i][j] 改为这个值,并将PATH[i][j] 置为 %s" % (k, k, k, k))for i in range(0, self.n):for j in range(0, self.n):if A[i][j] > A[i][k] + A[k][j]:A[i][j] = A[i][k] + A[k][j]Path[i][j] = kprint("A = \n", mat(A))print("PATH = \n", Path)return A, Pathstate2 = [[0, 5, inf, 7],[inf, 0, 4, 2],[3, 3, 0, 2],[inf, inf, 1, 0]]G = MGragph(state2)A, Path = G.fuluoyide()
最后返回的数组是
A =[[0 5 8 7][6 0 3 2][3 3 0 2][4 4 1 0]]PATH =[[-1 -1 3 -1][ 3 -1 3 -1][-1 -1 -1 -1][ 2 2 -1 -1]]# 矩阵A 代表 任意两点的最短路径长度# 矩阵PATH 代表 任意两点之间最短路径# 比如求 1 到 3 的路径与长度# 查表 A[1][5] = 2# 查表path的 PATH[1][6] = -1 表示直接相连# 比如求 1 到 0 的路径与长度# 查表 A[1][0] = 6# 查表path的 PATH[1][0] = 3 则3作为下一步起点# PATH[3][0] = 2 则2作为下一步的起点# PATH[2][0] = -1 查找结束 最终路径为 1 -> 3 -> 2 -> 0
附上该题目的图片
性能分析
- 复杂度
贝尔曼福特算法
http://www.cnblogs.com/gaochundong/p/bellman_ford_algorithm.html
http://www.wutianqi.com/?p=1912
算法思想:
Bellman-Ford算法能在更普遍的情况下(存在负权边)解决单源点最短路径问题。对于给定的带权(有向或无向)图 G=(V,E),其源点为s,加权函数 w是 边集 E 的映射。对图G运行Bellman-Ford算法的结果是一个布尔值,表明图中是否存在着一个从源点s可达的负权回路。若不存在这样的回路,算法将给出从源点s到 图G的任意顶点v的最短路径d[v]。
算法流程:
1. 初始化:将除源点外的所有顶点的最短距离估计值 d[v] ←+∞, d[s] ←0;
2. 迭代求解:反复对边集E中的每条边进行松弛操作,使得顶点集V中的每个顶点v的最短距离估计值逐步逼近其最短距离;(运行|v|-1次)
3. 检验负权回路:判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false,表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在 d[v]中。
核心算法就是
- 对于一个包含n个顶点,m条边的图, 计算源点到任意点的最短距离
- 循环n-1轮,每轮对m条边进行一次松弛操作
算法实现
G = {1: {1: 0, 2: -3, 5: 5},2: {2: 0, 3: 2},3: {3: 0, 4: 3},4: {4: 0, 5: 2},5: {5: 0}}def getEdges(G):""" 输入图G,返回其边与端点的列表 """v1 = [] # 出发点v2 = [] # 对应的相邻到达点w = [] # 顶点v1到顶点v2的边的权值for i in G:for j in G[i]:if G[i][j] != 0:w.append(G[i][j])v1.append(i)v2.append(j)return v1, v2, wclass CycleError(Exception):passdef Bellman_Ford(G, v0, INF=999):v1, v2, w = getEdges(G)# 初始化源点与所有点之间的最短距离dis = dict((k, INF) for k in G.keys())dis[v0] = 0# 核心算法for k in range(len(G) - 1): # 循环 n-1轮check = 0 # 用于标记本轮松弛中dis是否发生更新for i in range(len(w)): # 对每条边进行一次松弛操作if dis[v1[i]] + w[i] < dis[v2[i]]:dis[v2[i]] = dis[v1[i]] + w[i]check = 1if check == 0: break# 检测负权回路# 如果在 n-1 次松弛之后,最短路径依然发生变化,则该图必然存在负权回路flag = 0for i in range(len(w)): # 对每条边再尝试进行一次松弛操作if dis[v1[i]] + w[i] < dis[v2[i]]:flag = 1breakif flag == 1:# raise CycleError()return Falsereturn disv0 = 1dis = Bellman_Ford(G, v0)print(dis.values())
拓扑排序与AOV
算法思想:
AOV网是一种以顶点表示活动,以边表示先后次序且没有回路的有向图。
算法流程:
- 从有向图中选择一个没有前驱(入度为0)的顶点输出。
- 删除之前选择的顶点,并删除这个点出发的边
- 重复上述过程,直到不存在没有前驱的顶点为止
算法分析:
- 拓扑排序结果可能不止一个
- 当有向图无环的时候,还可以用DFS进出栈的过程模拟拓扑排序。 这个很有意思
- 时间复杂度
关键路径与AOE
与AOV的对比
- 同
- 两者都是无环图
- 异
- AOE的边表示活动,有权,代表活动持续时间
- AOV的边代表活动,无权
对于一个工程的AOE网,只存在一个入度为0的点,成为源点。也只存在一个出度为0的点,表示汇点
2. 错题摘录
DFS好像有点糊涂,到时候问问室友
- 图中有关路径的定义: 由相邻顶点序偶所形成的序列。
- DFS和BFS对于所有图都使用
- 当各边的权值均相等的时候,可以用BFS算法来解决最短路径问题(可以自己想一下为啥)
- 有向图G拓扑序列。如果顶点在之前,那么G中不可能有一条从到的回路。
- 如果一个图从任意一个顶点出发,用DFS可以遍历所有节点,那么这个图一定是连通图。
- 尽管对于一个图而言,可能DFS的访问序列有多个,但是如果是用邻接表表示这个图的话,DFS的遍历序列只可能有一个。(邻接表访问是有顺序的)
- 利用DFS或者拓扑排序可以判断出一个有向图是不是有环。
- 为啥?
- 对于拓扑排序,如果最后删得剩下的不止一个顶点,那么就有环了。
- 对于DFS,如果从某个顶点v出发,在dfs(v)结束前出现了一条从j指向v的路径,那么就必然存在环
- 若路径中除了开始点和结束点可以相同外,其他的顶点均不相同,则称这条路径为简单路径。很明显的是,回路和简单路径的概念完全不同
- 在用邻接矩阵代表无向图的时候,各顶点纵向与横向非零元素和尾顶点的度。不要傻不拉几的画个图
- ...
3. 总结
到时候需要做的事情
- AOE 找个题目做一做
- DFS 有点迷糊,找人问懂
- 书上好像没有贝尔曼福特,到时候再看看
- 找个时间手写一下各个算法的过程。要求无误。
0x02 查找
1. 概念梳理
直接插入排序
每一趟将待排序的关键字插入已经排好的部分序列上的合适位置上
- 时间复杂度 最好情况为 (序列完全有序)
- 时间复杂度
折半插入排序
和直接插排相比,插入的时候按照折半查找的方法进行。(mid为low+high除以2向下取整),要修改high则为high=m-1,要修改low则为low=m+1
- 时间复杂度(平均) 最好情况
- 时间复杂度
希尔排序
将待排序序列切成若干个子序列,并设定增量。比如说d = 5,则将下标为的分为一组,的分为一组,如此类推。然后对各个子序列进行排序。然后再缩小增量进行排序,以此类推。
- 时间复杂度
- Shell 提出的:每次增量除以2向下取整,时间复杂度为
- 实际上时间复杂度的计算巨复杂,人家考研书上都说了不考,留给别人折腾去吧
- 增量序列的最后一个值一定是1
- 增量序列的值尽量没有除了1以外的公因子
- 空间复杂度
- 希尔排序是不稳定的
冒泡儿排序
- 时间复杂度(平均) 最好情况
- 空间复杂度
快速排序
以前写过一个,不过方法和书上不太一样。我还是按照课本上说的来,具体如何实现的,这边不赘述了。
https://www.zybuluo.com/shaobaobaoer/note/1151376
- 时间复杂度(平均) 最坏情况(序列完全有序)为
- 空间复杂度 需要栈来辅助
简单选择排序
将序列切割成有序和无序两个部分,从无序的部分中选择出一个最小的(最大的)
- 时间复杂度
- 空间复杂度
堆排序
参考 https://www.cnblogs.com/chengxiao/p/6129630.html
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
堆
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
堆的定义
- 大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
- 小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
【升序大顶堆,降序小顶堆】
堆还是上个学习学的东西,总之,调整是从第一个非叶子节点开始,从左到右,从下到上调整。第一趟调整完后,将第一个元素和最后一个元素互换,并将最后一个元素弹出并压栈,第一趟堆排完成。
之后将剩余元素继续重复上述步骤,直到就剩下一个元素的时候,排序结束。最后把栈中元素弹出。得到升序序列。
总结来说,就是这样的:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
- 时间复杂度
- 空间复杂度
- 适用场合 从 1000 个中选出前5个最小的。
二路归并排序
- 对于有n个元素的序列,先把它看成有n个关键字的子序列,显然这些都是有序的
- 之后两两归并,这样就有了 个子序列,(最后一个序列可能只有1个元素),并对他们排序
- 继续两两归并,可以得到若干有序的四元组,依次递归,直到排序完成
- 时间复杂度 与初始序列无关,平均情况(也是最好和最坏的情况)
- 空间复杂度
基数排序
这个玩意儿比较魔幻,稍微多写点。
基数排序的思想是多关键字排序,又称为桶排序,通过使用对多关键字进行排序的分配与收集。将无序序列排列成有序序列。
e.g
初始序列:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 278 | 109 | 063 | 930 | 589 | 184 | 505 | 269 | 008 | 083 |
对于数字而言,需要十个桶,代表关键字0-9,第一趟排序,将序列按照最低位入桶。
注意
数字要有序放入,放入方式就像是入栈一样,这也是为啥109在最下面,269在最上面
出桶的顺序和出栈顺序相反,按照桶的次序从桶下方依次取出。桶是一个队列
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 930 | 083 063 |
184 | 505 | 008 278 |
269 589 109 |
得到序列如下:
930 063 083 184 505 278 008 109 589 269
然后对上述序列按照中间位入桶,得到的序列如下:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 109 008 505 |
930 | 269 063 |
278 | 589 184 083 |
出桶得序列如下:
505 008 109 930 063 269 278 083 184 589
最后对上述序列按照最高位入桶,得到的序列如下:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 083 063 008 |
184 109 |
278 269 |
589 505 |
930 |
出桶得序列如下:排序完成
008 083 063 109 184 269 278 505 589 930
- 序列中的关键字字数 (序列长度)
- 序列中关键字的位数 (排几次)
- 关键字基的个数 (就是有几个桶)
- 时间复杂度 平均和最坏情况
- 空间复杂度
--*--
- 外部排序 <这个以后有空再看>
- 选择置换排序
- 最佳归并树
- 败者树
关于时间与空间复杂度的问题
先附上PPT
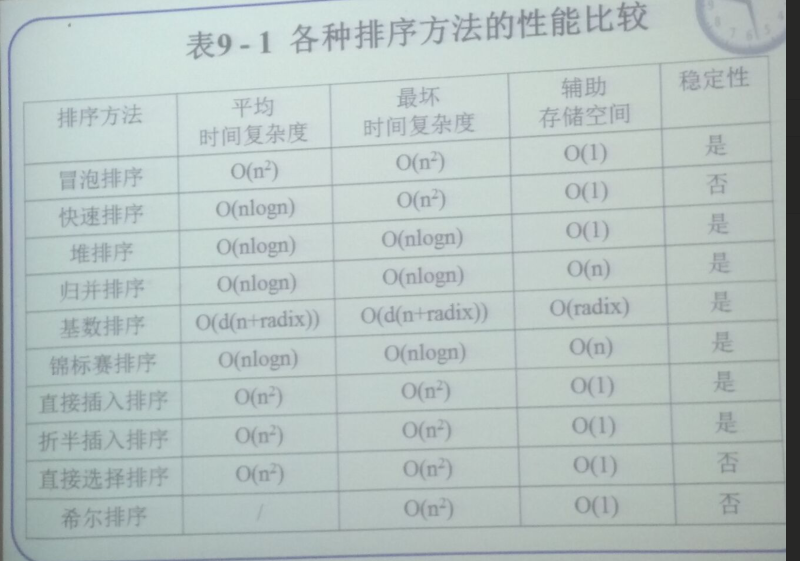
相当重要[1]
- 时间复杂度
- 快
<快排>些<希尔>以的速度归<归并>队<堆排> - 这四个都是别的都是
- 只有快排有最坏情况,为 4
- (序列完全有序的情况)
- 快
- 空间复杂度 快排 归并 基数 别的都是O(1)
- 稳定
- 数据结构复习好痛苦,情绪不稳定,快
<快排>些<希尔>选<选择>一堆<堆排>好友聊天
- 数据结构复习好痛苦,情绪不稳定,快
- 排序算法的关键字比较次数与原始序列无关的 ———— 简单选择排序和折半插入排序(考卷上还遇到了基数排序)
- 排序算法的排序趟数和原始序列有关的 ———— 交换类排序
- 经过一趟排序,能够保证一个关键字到达最终位置,这样的排序是交换类的冒泡和快速,以及选择类的简单选择与堆排
2. 错题摘录
- 选择排序和插入排序的区别。
- 插入排序和选择排序都有两层循环,外循环遍历整个数组,内循环稍有区别:
- 选择排序 的内循环是遍历一组未排过序的数组,
- 插入排序 的内循环是遍历一组已排过序的数组,
- 希尔排序与归并排序的区别:
- 主要体现在切割方法上
- 希尔排序 是按照增量来切割序列,然后会这些子序列进行排序,然后再把排序号的子序列合并成朱序列。接着,按照来切割序列,对这些子序列排序
- 二路归并排序 是按照2,4,6,...,n的顺序把主序列分成若干组,然后对这些组排序。
- 主要体现在切割方法上
- 冒泡儿和直接选择排序,在序列完全有序的时候时间复杂度为 但是,当序列完全有序的时候,快排的空间复杂度最高,为
- 希尔排序不能保证每趟排序至少能够将一个关键字放到其最终位置上。
- 在堆排序插入的时候,当问及关键字的比价次数,那么只要数被影响的部分的比较次数就行。
- e.g. 已知大顶堆 25,13,19,12,9 插入18,再次调整为大顶堆,调整过程中关键字之间的比较次数为 2 次。
- 快排的递归次数与每次划分后得到的分区的处理顺序无关,这意味着快排的最下面两个递归的位置可以互换,不会影响结果。
3. 总结
To be continue
0x03 排序
1. 概念梳理
概念,顺序与折半
顺序查找 && 折半查找
- 顺序查找的
- 折半查找的 近似。 其实求折半查找的ASL的应该建立折半查找树,然后进行精确的运算才行。如果要取整数的话,已知折半查找树的高度不大于[上取整]。所以平均查找长度为
折半查找树
二叉排序树与平衡二叉树
二叉排序树
- BST定义
- 左子树不空,则左子树上所有关键字的值均小于根关键字的值
- 右子树不空,则右子树上所有关键字的值均大于根关键字的值
- 左右子树又是一颗BST
- BST 的插入,查找 略
- BST 的删除
- 如果p是叶子节点直接删了就行
- 如果p只有左子树或者只有右子树,那就把p删了,把其子树连上去
- 如果p 既有左子树,又有右子树 那就沿着p的左子树的右指针一直往右走。找到节点r,把p的关键字用节点r的关键字代替,并判断r的情况,用上述两种方法中的一种删除r。
- 其实往右子树的左指针一直往左走也是可以的,但是为了规范,记忆的时候采取上述方法
平衡二叉树
- AVL 定义
- 特殊的二叉排序树,左右子树高度之差的绝对值不超过1
- 平衡因子 左子树高度减去右子树高度的差,对于平衡二叉树,平衡因子的取值只能是-1 0 1
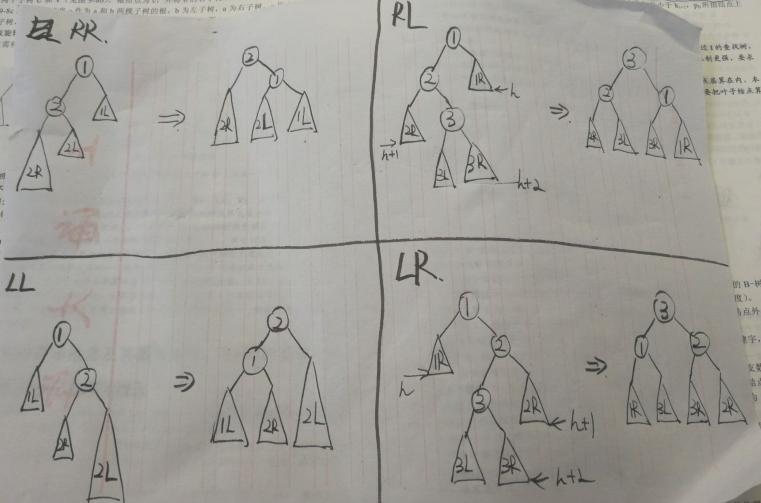
- 平衡调整 重点!!!
- LL
- RR
- LR
- RL
- 具体如何实现,看图[emmm 将就着看吧 LL 和 RR 写反了]
- 冷门知识:平衡二叉树至少有几个节点。
- 平衡二叉树的最少节点类似菲波那切数列,也就是:
- 平衡二叉树的最少节点类似菲波那切数列,也就是:
B+ 与 B- 树
B+树似乎不考
B-树
具体看书吧,我这边写的不是很全,动手画一画,把删除,插入,建立的操作都画一遍,会有新的感悟!
- B-T 定义
- 满足以下要求的 m 叉树
- 每个节点最多有m个分支。根节点且不是叶子节点,那就至少要有两个分支,非根非叶节点,至少有[m/2<上取整>]个分支
- 如果B-T的阶数为m 那么节点的关键字个数的范围是 ⌈m/2⌉ -1 ~ m-1 分支数S的范围是 ⌈m/2⌉ ~ m
- B-T 建立
- B-T 删除
- 向兄弟借关键字。当删除关键字后,该节点所在的关键字个数小于[m/2],需要向旁边的兄弟借关键字。采用不同的合并方法将产生不同的B-T
- 如果删除的关键字不在终端节点上,要把它转化为终端节点
- B-T 插入
- 插入位置一定出现在终端节点上,插入只会让树变高,而不会改变叶子节点在同一层的特性。
B+树
B+ 树n个关键字有n个分支,比B-T少一个
散列表
哈希表查找不成功和成功的ASL 如何计算?
https://blog.csdn.net/u013806583/article/details/52643541
概念
根据给定关键字来计算出关键字的地址。(python的字典2333)
装填因子与确定表长
- 装填因子 a
- 通过装填因子可以确定表长。公式为
- 如果Hash函数的值没有给出,一般取不大于表长的最大素数。
常见的Hash函数构造方法
- 直接定址
- 数字分析
- 平方区中
- 除留余数法
常见冲突的解决方法
- 开放地址法
- 线性探测,有冲突了就用递推公式解决问题,容易产生堆积问题。公式为
- 平方探查,有冲突了就,不能探查到所有元素,但是能够探查到至少一半的单元。
- 双Hash 算两次哈希函数
- 线性探测,有冲突了就用递推公式解决问题,容易产生堆积问题。公式为
- 链地址法
- 二次探测法(某大学书上介绍的一种野路子) 其实这玩意就是平方探查法
- 当发生冲突的时候,寻找下一个元素的公式为
- 其中
- 其中 为表的大小(长度)
2. 错题摘录
- Hash函数有一个共同的性质:函数值应当以同等概率取其值域的每一个值
- 平衡二叉树的最少节点类似菲波那切数列,也就是:
- 这就意味着,在平衡二叉树,如果给定了节点数,那就可以确定平衡二叉树的高度
- 哈希查找的时间复杂度为 因为这个是散列表
0x04 考卷陌生题解析
并查集
- 每个等价类用一棵树表示,用树的根节点来代表相应的等价类。等价类树用双亲表示法表示。
上学期的一些比较有用的结论
含有n个节点的二叉树的高度范围在 之间
在插入排序的时候,元素是从后往前比较,而不是从前往后比较
https://www.nowcoder.com/questionTerminal/22576bafa4d64135a5ace210bfad2c92
(12-13.三.10) 对一组记录(54,38,106,21,15,72,60,45,83)进行直接插入排序时,当把第7个记录60插入到有序表时,为寻找插入位置需比较(3)次
在插入第7个数,说明前面的数字已经有序了。
即数字为[15--- 21---38---54----72---106--]--60---45---83
现在对第7个数字60进行插入,需要向前找到插入点。依次比较,96,72,54.最后插入在54后面。
所以比较3次。
(12-13.一.1) 不是每一棵二叉树都可以转化成树表示
(12-13.一.4) B-树删除某一关键字值时候,不会引起节点的分裂
(12-13.二.1) 分块查找,既能较快查找,又能适应动态变化
(15-16.一.9) 了解一下临接多重表的画法等,之前没有复习到
(15-16.一.2) 带权连通图G,权值最小的边一定包含在最小生成树中
(15-16.一.4) 

- 一个节点一个入度,那么,现在总节点个数为 。已知现在共有 个节点已经分配到了一个入度,那么剩下的节点就都是根节点了,一共
- 还有一种方法,就是一步步推,把四叉树每一层有多少个节点推算出来。也是一种方法。
(15-16.三.2) 希尔排序的时间复杂度与增量的选取有关。希尔提出的增量复杂度为,增量选取公式为 后俩又有两个大大提出了一种的增量序列,其十几件时间复杂度为。希尔排序的时间复杂度算起来很麻烦,不要求掌握,知道即可。
(15-16.三.5) 无论是DFS还是BFS,都不能完全遍历无向图中的所有顶点。很简单,如果这个无向图的连通分量大于等于2的话,就只能遍历一部分了。
(15-16.四) 已知Hash = key mod 9 ;二次探测(平方)探测。求 成功和失败的ASL

- 求失败的时候,需要知道key从0-8的查找长度。可以求得如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 2 | 1 | 2 | 1 | 3 | 4 | 10 | 4 | 2 |
- 这里说一下5咋算的,其余类似
5 mod 10 = 5 ;a[5]!=NULL;value=1;5 + 1^2 = 6 ;a[6]!=NULL;value=2;5 - 1^2 = 4 ;a[4]!=NULL;value=3;(5 + 4) mod 10 = 9;a[9]==NULL;OUTPUT value=4;
0x05 算法设计题
我一个搞信安的。做算法填空设计啥的真是头大。这里给菜鸡的自己记录一些小技巧。ACM大佬们不要喷我。以下模板基本上都是我YY出来的,有啥错的还请指正。
邻接矩阵,邻接表,邻接多重表
> 自己看书
这边说一个很恐怖的事情,根据SJ的模板,他对这三个词语的英文称呼如下;严版的英文称呼在后头
- 邻接矩阵 Adj_Matrix_Undir(Dir)_Graph | MGraph
- 邻接表 Adj_List_Dir(Undir)_Network(Graph) | AGraph
- 邻接多重表 ...
邻接矩阵封装的方法
我乖乖看sj的书还不行么...
| vertexes | tag | arcs | vexNum | vexMaxNum | arcNum |
|---|---|---|---|---|---|
| 图中顶点信息<Array[]> | 访问情况<Array[]> | 二维矩阵 <Array[ ][ ]> |
//
邻接表封装的方法
我乖乖看sj的书还不行么...
| data | firstarc |
|---|---|
| 顶点的值 | 指向边节点 |
| adjvex | (weight) | nextarc |
|---|---|---|
| 顶点 | 权 | 指向下一个边节点 |
二叉树先序遍历模板
为啥写这个呢?因为把二叉树的遍历延伸出去,就是DFS(先序),也可以是二叉排序树的遍历
void preorder(btnode *p){if(p!=NULL){visit(p);preorder(p->left);preorder(p->right);}}
DFS
\\ 强行按照sj的封装函数魔改了一波void DFS(AGraph &g, int v){visit(v);g.SetTag(v, VISITED);for (int w = g.FirstAdjVex(v); w != -1; w = g.NextAdjVex(v, w))if (g.GetTag(w) == UNVISITED) DFS(g, w);}
扩展DFS检测环
能够检测出一个有向图是否存在环,除却利用拓扑排序(最后删得剩下两个入度为0的顶点且无关联)外,还可以用魔改的DFS算法,在该DFS中,需要对回边进行检测,如果回边为VISITED,那么就检测到环。
\\ 我按照自己的想法写的,如果有问题还请大神指正。bool Cycle_DFS(AGraph &g, int v,int pre){// visit(v);// ifg.SetTag(v, VISITED);for (int w = g.FirstAdjVex(v); w != -1; w = g.NextAdjVex(v, w))if (g.GetTag(w) == UNVISITED) Cycle_DFS(g, w);}
二叉树层序遍历模板
为啥要写这个呢? BFS的思路就是层序遍历。延伸出去,也可能是B-树或者B+树的遍历。
void layorder(btnode *p){if (p==NULL) return ;Queue<Type> Q;btnode *m;Q.enqueue(p);while(!Q.empty()){m=Q.dequeue();visit(m);if(m->left!=NULL)Q.enqueue(m->left);if(m->right!=NULL)Q.enqueue(m->right);}}
BFS
\\ 强行按照sj的封装函数魔改了一波;行...一切按大哥的来void BFS(AGraph &g, int v){Queue<Type> Q;int m;g.SetTag(v, VISITED);visit(v->data);Q.enqueue(v);While(!Q.empty()){m = Q.dequeue();for (w = g.FirstAdjVex(m); w != -1; w = g.NextAdjVex(m, w)){g.SetTag(w, VISITED);g.GetElem(w, e);Visit(e);Q.EnQueue(w);}}}
