根据上市公司若干财务指标,分析是否存在风险

DM

01.data_190317.xlsx 是原始数据. 样本数为$N=502$.

实验一,二,三

预处理:

选取了除两个分类以外的所有特征列. 特征数$M=18$. 则所有特征数据记为$X\in \Re^{N \times M}$. $x_{ij}$表示第i个样本的第j个特征.
特征的顺序为: 'X20', 'X1', 'X2', 'X3', 'X4', 'X5', 'X6', 'X7', 'X8', 'X9', 'X10', 'X11', 'X12', 'X13', 'X14', 'X15', 'X16', 'X17'.
$X=(x_1, x_2,...,x_m)$, 其中每个$x_j$为一个N维列向量.
首先对每个$x_j$做中心化处理: $x_j \Leftarrow x_j-\frac 1 N\sum_{i=1}^N x_{ij}$
中心化后的$X$记为$XC$

计算$XC$的相关系数矩阵

02.cor1.xlsx

对相关系数矩阵做kmo检验值, bartlett检验值, levene检验值

03.各种因子检验-ALL.txt

kmo: 0.6548698404468887
bartlett: statistic=49182.35560796065, p==0.0
levene: statistic=23.074111365187676, p==3.5517548881872756e-71

对$XC$做PCA分解, 得到各主成分的方差和方差占比

04.pca_var-ALL.xlsx
第一列是主成分序号, 第二列是各主成分的方差, 第三列是方差占比
各成分方差碎石图:

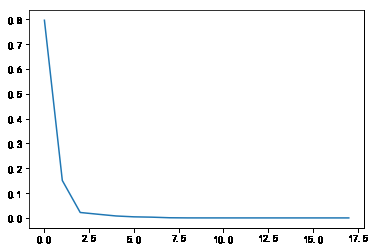
05.pca-碎石图-ALL.png

各主成分的特征向量如下:

06.pca_cmpts-ALL.xlsx
每行是一个主成分, 列是主成分中每个原始特征的权重. 颜色越红越正相关, 越绿越负相关.
可以用这个对每个主成分做一定的解读.

逻辑回归

由于样品偏斜很严重(正样品22个, 负样本480个), 因此为正样本($Y=1$)设置了$502/(2\times22)$, 为负样本($Y=0$)设置了$502/(2\times480)$
正则项强度设置为0.001. 这一点不一定要在论文里提到, 这是因为反正不做交叉验证, 所以不必考虑训练集以外的表现, 所以正则强度设置的非常小.

实验一

选取前9个主成分, 使用liblinear库训练, 使用L2损失函数. 迭代21次后收敛.
9个成分的权重如下:
07.COE B=22-480C=1000PCA=9.xlsx

将分类阈值从0到1, 以0.01为单位步进, 分别测量查准率, 召回率, $F_\beta$, 准确率.

$F_\beta$的$\beta$的经验值定为: $\log(480/22)\approx3.08$. 下同

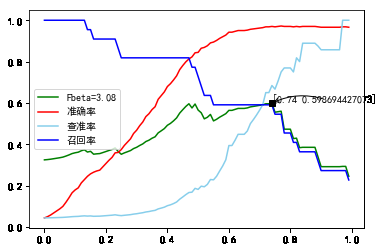
08.B=22-480C=1000PCA=9.png
取$F_\beta$最大处, 分类阈值为0.74. 详细预测结果如下:
09.B=22-480C=1000HC=0.74PCA=9.xlsx

查准率: 0.684211, 召回率: 0.590910, $F_\beta$: 0.598694, 准确率: 0.970120

实验二

选取前14个主成分, 使用liblinear库训练, 使用L2损失函数. 迭代24次后收敛.
14个成分的权重如下:
10.COE B=22-480C=1000PCA=14.xlsx

将分类阈值从0到1, 以0.01为单位步进, 分别测量查准率, 召回率, $F_\beta$, 准确率.

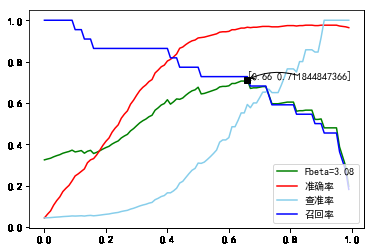
11.B=22-480C=1000PCA=14.png
取$F_\beta$最大处, 分类阈值为0.66. 详细预测结果如下:
12.B=22-480C=1000HC=0.66PCA=14.xlsx

查准率:0.592593, 召回率: 0.727273, $F_\beta$: 0.711845, 准确率: 0.966135

实验三

选取所有主成分, 使用liblinear库训练, 使用L2损失函数. 迭代43次后收敛.
所有成分的权重如下:
13.COE B=22-480C=1000PCA=ALL.xlsx

将分类阈值从0到1, 以0.01为单位步进, 分别测量查准率, 召回率, $F_\beta$, 准确率.

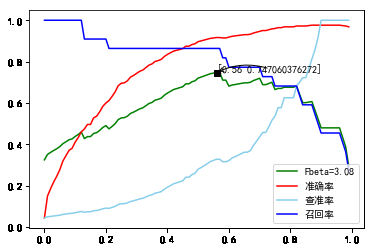
14.B=22-480C=1000PCA=All.png
取$F_\beta$最大处, 分类阈值为0.56. 详细预测结果如下:
15.B=22-480C=1000HC=0.56PCA=All.xlsx

查准率:0.327586, 召回率: 0.863636, $F_\beta$: 0.747060, 准确率: 0.916335

以上对比实现可以看出, 对以上数据来说, 逻辑回归模型已有足够的表达能力, 无需使用PCA降维, PCA的作用仅在于加快训练阶段的速度. 这个要不要写进论文不好说....

实验四,五

数据预处理.

在以上实验数据的基础上, 加入两个分类特征, 使用one-hot编码后, 中心化.

16.data2.xlsx
相关系数矩阵
17.cor2.xlsx

球形检验, levene检验:

bartlett: statistic=98081.56759920045, p==0.0
levene: statistic=25.493861566441822, p==2.085507891134541e-124

PCA分解, 主成分方差和占比:
18.d2_pca_var.xlsx
碎石图

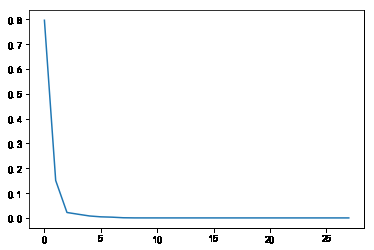
19.d2-pca-碎石图-ALL.png

各主成分中原始特征权重
20.d2_pca_cmpts.xlsx

前12个主成分中, 两个分类相关的字段权重十分小, 说明行业和性质分类对总体方差贡献相对较小, 重点使用其他指标是对的. 但这仅仅是从数据本身的角度看, 如果有标签的话, 就是另外一回事了.

实验四

选取所有主成分, 使用liblinear库训练, 使用L2损失函数. 迭代51次后收敛.
所有成分的权重如下:
21.d2 COE B=22-480C=1000PCA=ALL.xlsx

将分类阈值从0到1, 以0.01为单位步进, 分别测量查准率, 召回率, $F_\beta$, 准确率.

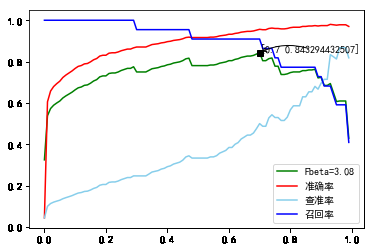
22.d2 B=22-480C=1000PCA=All.png
取$F_\beta$最大处, 分类阈值为0.7. 详细预测结果如下:
23.d2 B=22-480C=1000HC=0.7PCA=All.xlsx

查准率:0.5, 召回率: 0.909091, $F_\beta$: 0.843294, 准确率: 0.956175

增加类型信息后, 各个指标均有一定的提高

实验五

选取前18个主成分, 使用liblinear库训练, 使用L2损失函数. 迭代33次后收敛.
所有成分的权重如下:
24.d2 COE B=22-480C=1000PCA=18.xlsx

将分类阈值从0到1, 以0.01为单位步进, 分别测量查准率, 召回率, $F_\beta$, 准确率.

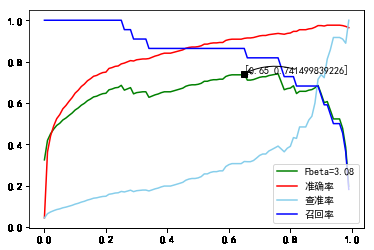
25.d2 B=22-480C=1000PCA=18.png
取$F_\beta$最大处, 分类阈值为0.65. 详细预测结果如下:
26.d2 B=22-480C=1000HC=0.65PCA=18.xlsx

查准率:0.316667, 召回率: 0.863636, $F_\beta$: 0.7415, 准确率: 0.912351