第四次作业

计算物理作业 人口增长模型

一、题目选择

• 选择的题目为第一章课后题第六题“人口增长模型”
• Population growth problems often give rise to rate equations that are first order.For example,the equation
  $$\frac{dN}{dt}=aN-bN^2$$ might describe how the number of individuals in a population,N,varies with time.Here the first term $aN$ correspond to the birth of new members,while the second term $-bN^2$ corresponds to deaths.The death term is proportional to $N^2$ to allow for the fact that food will become harder to find when the population $N$ becomes large.

二、欧拉法推导算法

• 由题目给的微分方程可知：
  $$\frac{N(t+\Delta t)-N(t)}{\Delta t}\approx [aN(t)-bN^{2}(t)]$$ 由欧拉方法可近似： $$N(t+\Delta t)\approx [aN(t)-bN^{2}(t)]\times \Delta t+N(t)$$
• 同时我希望能得到人口增长的速率，从数学上这是人口数$N(t)$的导函数，我将它定义为 $p$，有 $$p(t)=aN(t)-bN^{2}(t)$$

三、程序模拟

• 首先我模拟了人口的增长模型，假设初始时 $N(0)=1$，运行程序得到图像

代码链接

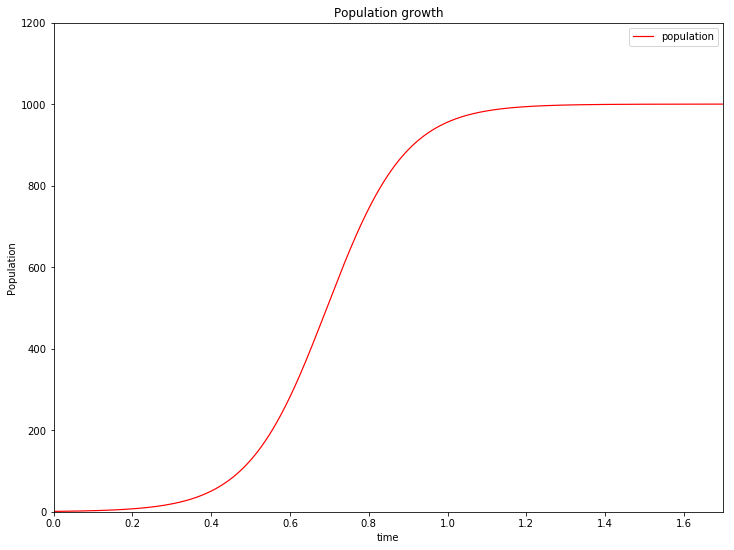
可见，人口数量经过了一个由缓慢、快速、再到缓慢，最后趋于稳定值 1000 的图像，惊奇的发现这就是高中生物书上的马尔萨斯模型！

接着我又计算了人口的增长速率，只需要在源代码中加入一个初值为 0 的变量稍加修改就可以了

代码链接

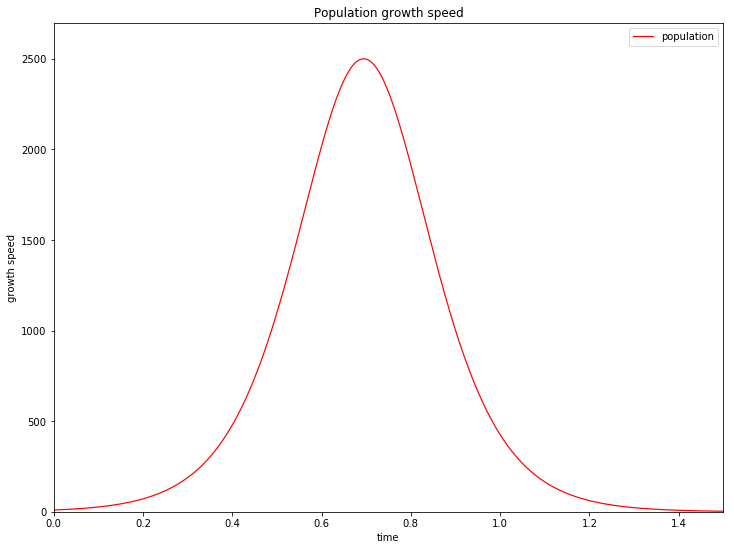
上图反应的特点可以这样解释：开始时由于环境广阔、食物充裕，人口快速增长，同时由于人变多了增长速率进一步加快，很快达到速率峰值。但随着人口不断增加，生存空间越来越小，使的人口增长速率变缓，最后趋于 0，此时人口数量也趋于稳定。

• 接下来我计算了人口减少的衰退型模型，假设初始人口 $N(0)=2000$ ,此时的人口大大的超过了环境的承受量，于是得到了如下图像

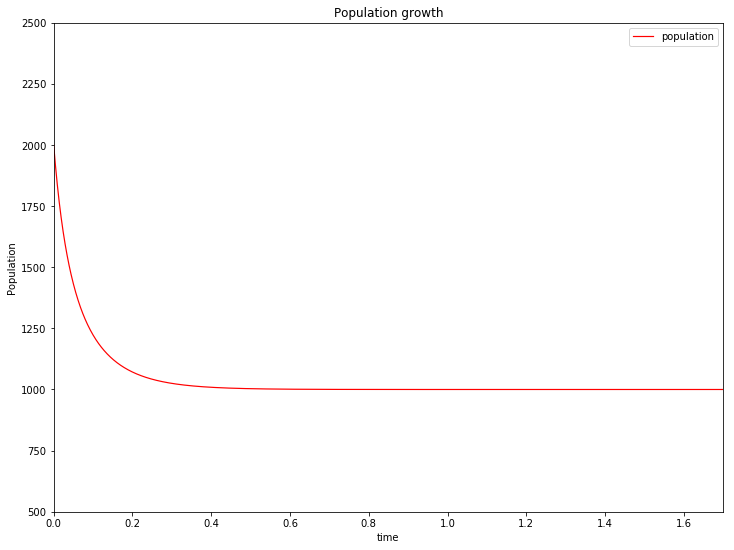
人口在开始时迅速下降，并最终趋于稳定值1000

四、问题及讨论

在运行人口减少的程序时，中途出现了这样一个图像

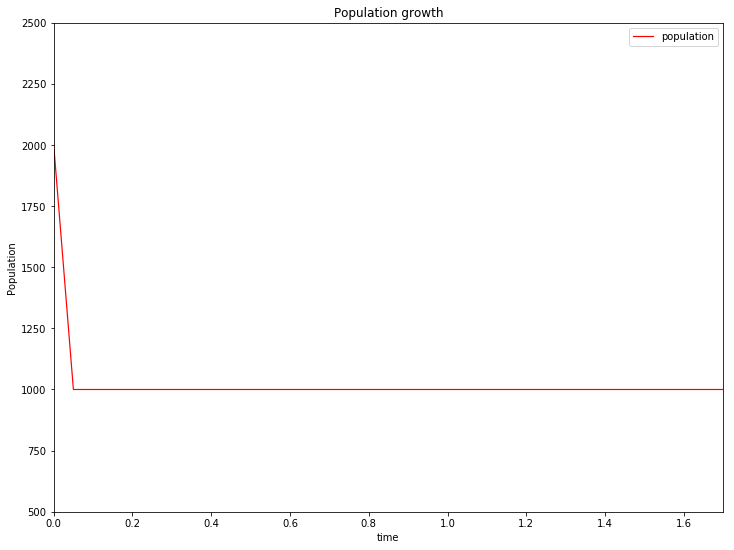
人口数量曲线并不平滑，出现了非常生硬的折线。经过分析我找到了原因

N=[]            #population
t=[]            #time
a=10            #assign a value to a
b=0.01          #assign a value to b
det_t=0.5     #time step
N.append(1)     #assign a value to first item of v[]
t.append(0)     #assign a value to first item of t[]
end_time=2      #total time

注意代码中的det_t=0.5，这个时间间隔太大了，由于初始时$N=2000$，所以初始时人口下降速度非常快，如果此时时间间隔太大，人口数量将缺少一个缓缓平稳的过程。所以欧拉方法也有它的弊端：所取时间间隔的大小直接决定了方程拟合的准确性，并且当函数的变化率非常大时对时间间隔的要求就更高了。

• 助教老师，由于我给蔡浩老师的软件池地址输错了一个字母，直到上周一我才更改过来，可能前几次作业您没能及时看到，希望您能补上成绩。