第六次作业

计算物理作业 棒球轨迹

一、摘要

• Problem 2.19:
  Model the effect of backspin on the range of a batted ball.Assume an angular velocity of 2000 rpm.
• 在考虑棒球自旋的情况下，计算击球的轨迹。本次作业原则上还是使用了欧拉法，因此在方法上没有创新，但第一次使用了Matplotlib的3D绘图功能。

二、棒球自旋对的受力分析

• 球的自旋会产生Magnus作用力，力的矢量量表达式为：
  $$\vec{F}_{M}=S_0\vec{\omega }\times \vec{v}$$
  现假设$\vec{\omega }$方向朝上，并考虑空气阻力，因此总微分方程为：
  $$\frac{dv_{x}}{dt}=-\frac{B_{2}}{m}vv_{x}$$
  $$\frac{dv_{y}}{dt}=-g$$
  $$\frac{dv_{z}}{dt}=-\frac{S_{0}v_{x}\omega }{m}$$
  由此可以很方便的由欧拉法模拟轨迹。

三、高远球的轨迹预测

• 在棒球运动中，使用球棒击球时可以打出高远球，假设击球角度为45°，为了探究球的自旋对轨迹的影响，我们使用计算机分别模拟了考虑自旋、不考虑自旋两种情况：
  代码链接
  

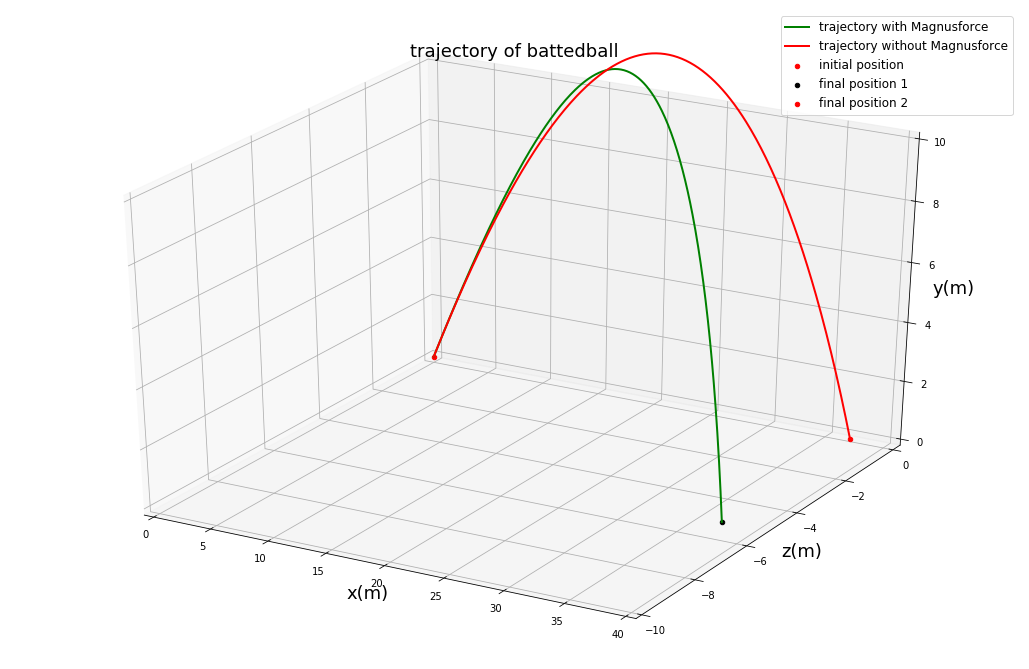
可以看到，相比没有自旋的球，有自旋的球在z方向可以产生明显偏差，为了更直接的看到两者的区别，我们取上方的俯视图：

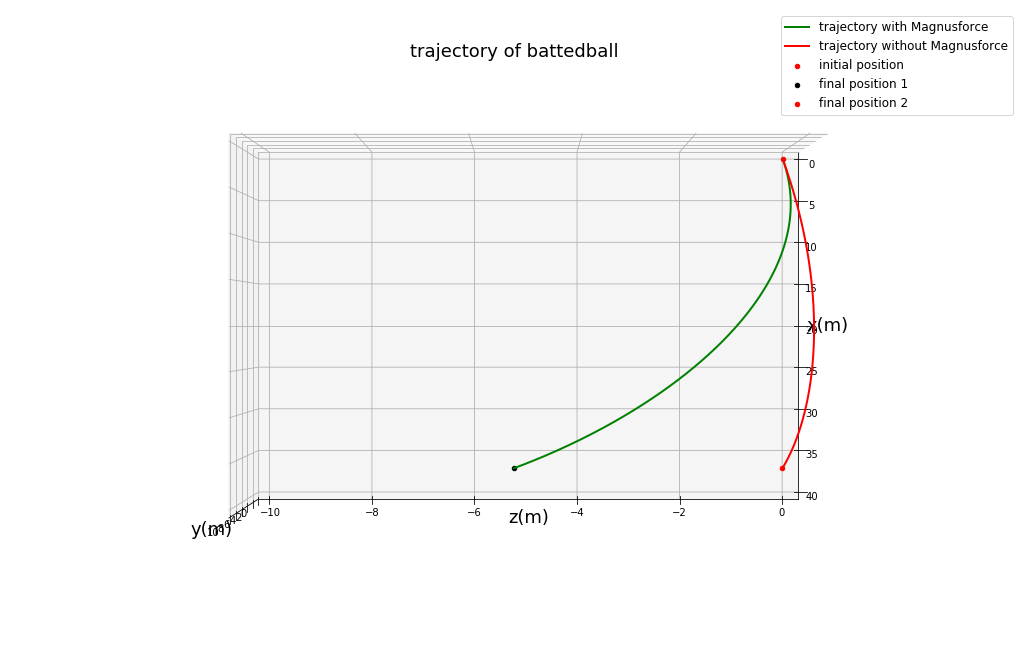
两者在z方向的落点偏差可以达到惊人的5米！这在棒球比赛中是十分客观的距离。

四、投掷球的轨迹预测

• 为了模拟棒球比赛中投球手的投球轨迹，我们又作了模拟。为了模拟投球的特点，我们设透出的球只有水平方向的速度，并且投球的位置有1米的高度。（因为此时的代码相比上面只是修改了速度数据，就不给出了）

同样给出俯视图：

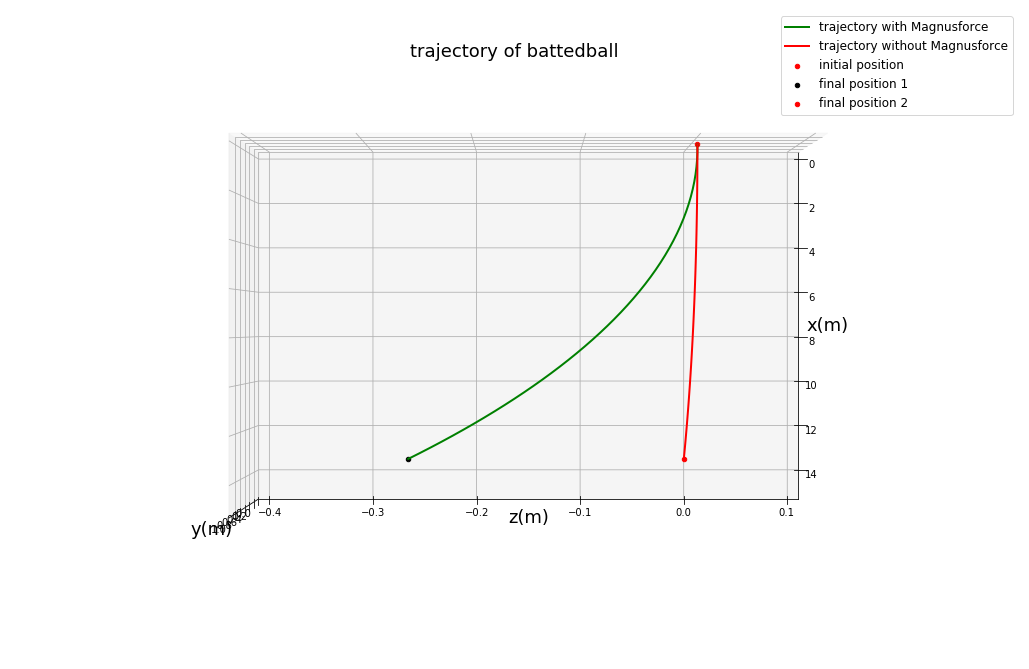
可以看到，对于水平投出的球，在z方向因为自旋引起的偏差并没有高远球那么大，大概在2.6米，但考虑到击球手离投球手的距离很近，适当的旋球可以对击球手造成威胁。

五、总结

• 从我们上面的讨论可以看到，自旋所带来的效应对棒球的轨迹影响非常大，同样的情形也可以用到乒乓球、炮弹的上。这是第一次3D制图，与制作2D的图像并无太大区别，可以看出Matplotlib功能的强大
  （感谢武汉理工大学的张志鹏为我提供技术支持！）