第四次作业——统计物理

热统 郭忠智2014301020087

---

4.1. Simple example
（a）在这个问题中，每一个微观态的概率相同，概率为$P_s=\cfrac{1}{\Omega},$ 又有$s_2=\pm1.$所以

$$\begin{align} \bar s_2&=\sum_{i=1}^{10}P_is_{2,i}\\&=\cfrac 1{10}[6(+1)+4(-1)] \\&=\cfrac 15 \end{align}$$
因为5个自旋的总能量应为$E=-\mu B.$而可达到的每一个微观态是等概率的，所以这5个自旋的均值应相同，均为1/5.
（b）只有一个自旋朝上，相应的总能量为$E'=3\mu B$,这和题中给的能量条件不符，所以这个微观态到达的概率为0.
（c）自旋1和自旋2均朝上，要使总能量为$E=-\mu B$,其他三个自旋必须为2个朝上，1个朝下，书橱满足条件的微观态共有3个，所以这个事件的概率为3/10.

4.2. Counting microstates
（a）4个无相互作用的自旋，即$N=4$,总能量为$E= -2\mu B$,只能是其中一个自旋朝下，其他3个自旋朝上，所以可达到的微观态共有$C_4^3=4$个;如果其中某一个特定自旋朝上，那其他3个必须是1个朝下2个朝上，其概率为3/4，某一个自旋特定朝下的的概率为1/4.
（b）$N=9，E=-\mu B$.则其中必须为5个自旋朝上，可达到的微观态数量为$C_9^4=126$，某一个自旋特定为朝上的概率为$\cfrac{C_8^4}{C_9^4}=70/126=5/9.$

4.3.Probability of particles moving in the sane direction
N=5,对于其中的某一个粒子而言，它网一个特定方向运动的概率为1/2，而这5个粒子相互不干扰，运动独立，所以他们共同朝一个方向运动的概率为$(\cfrac 12)^5=\cfrac 1{32}.$

4.4.An Einstein solid
（a）对于N=3，E=3的爱因斯坦固体，其可达到的微观态可以直接数出来，如下表所示：

microstate	red	white	blue
1	1	1	1
2	2	0	1
3	2	1	0
4	1	0	2
5	1	2	0
6	0	1	2
7	0	2	1
8	3	0	0
9	0	3	0
10	0	0	3

可见，共有10种，
利用式（7.3）：

$$\Omega=\cfrac{(E+N-1)!}{E!(N-1)!}\tag{7.3}$$
对于E=3，N=3有： $$\Omega(E=3,N=3)=\cfrac{5!}{3!2!}=10.$$
得证。
（b） $$\Omega(E=6,N=4)=\cfrac{9!}{6!3!}=84.$$
（c）由（a）中的表可知，红色粒子能量为1的概率为3/10.
（d）给定红色粒子能量为1，蓝色粒子能量为2的概率为1/3.

4.5.

$$\begin{align} \sigma^2&=\overline{(E_A-\overline E_A)^2}\\&=\overline{E_A^2}-\overline{E_A}^2\\&=(0\times \cfrac{7}{84})+(1\times \cfrac{12}{84})+(4\times \cfrac{15}{84})+\\&(9\times \cfrac{16}{84})+(25\times \cfrac{12}{84})+(36\times \cfrac{7}{84})-3^2\\&=\cfrac{84}{7}-9\\&=3. \end{align}$$
所以$\sigma=\sqrt{3}.$

4.6. Two Einstein solids in the contact
$N_A=4,E_A=10,N_B=4,E_B=2.$
于是有：

$$\begin{align} \Omega_A&=\cfrac{(10+4-1)!}{10!(4-1)!}\\&=286\\ \Omega_B&=\cfrac{(4+2-1)!}{(4-1)!2!}\\&=10 \end{align}$$
初始时刻的微观态数量为： $$\begin{align} \Omega_{tot}&=\Omega_A \times \Omega_B\\&=2860. \end{align}$$
（a）$P(E_A)=\cfrac{\Omega_A(E_A) \Omega_B(E-E_A)}{\Omega_{tot}}$
The probable values of $E_A$ are 12,11,10,9,8,7,6,5,4,3,2,1,0.
we have known
$$\Omega=\cfrac{(E+N-1)!}{E!(N-1)!}\tag{7.3}\\ \Omega_{tot}=\sum_{E_A}\Omega_A(E_A) \Omega_B(E_{tot}-E_A)$$
then we can caculate the value of $P(E_A)$ representively.
plot $P(E_A)$versus $E_A$:

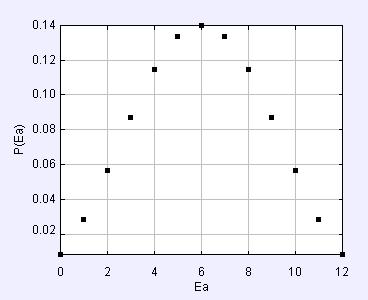
(b)The probability that the energy is transferred from system A to system B is $$P_1=0.9053,$$ from B to A it is $$P_2=0.0379.$$
And from the hotter to the colder system the probability is P1=0.9053，which is bigger than the smaller subsystems in Table4.3.
This system is hotter.
（c） $$\begin{align} \Omega_{tot}&=\sum_{E_A}\Omega_A(E_A) \Omega_B(E_{tot}-E_A)\\&=2\times[(455\times1)+(364\times4)+\\&(286\times10)+(220\times20)+(165\times35)+\\&(120\times56)]+(84\times84)\\&=50388 \end{align}$$
the initial entropy $$S_{init}=k\ln2860$$
when remove the internal constraint the entropy becomes
$$S_{latter}=k\ln50388$$
since $k=1$,the change in total entropy of the system is $$\Delta S=\ln{\cfrac{50388}{2860}}=2.8689$$
(d)
$P(E_A=12)=P(E_A=0)=\cfrac{455}{50388}=0.0903$
$P(E_A=11)=P(E_A=1)=\cfrac{364\times4}{50388}=0.0289$
$P(E_A=10)=P(E_A=2)=\cfrac{286\times10}{50388}=0.0568$
$P(E_A=9)=P(E_A=3)=\cfrac{220\times20}{50388}=0.0873$
$P(E_A=8)=P(E_A=4)=\cfrac{165\times35}{50388}=0.1146$
$P(E_A=7)=P(E_A=5)=\cfrac{120\times56}{50388}=0.1334$
$P(E_A=6)=P(E_A=6)=\cfrac{84\times84}{50388}=0.1400$
Then we get $$\overline{E_A}=6$$
and the most probable energy $$\hat E_A=6$$
the standard deviation $$\begin{align} \sigma_A&=\sqrt{\overline{(E_A-\overline E_A)^2}}\\&=\sqrt{\overline{E_A^2}-\overline{E_A}^2}\\&=\sqrt{54.3628-36}\\&=4.2852 \end{align}$$
$$\sigma_B=\sigma_A=4.2852$$
and the relevant fluctuations $$\cfrac{\sigma_A}{\overline{E_A}}=0.714$$
In the Table4.3 $\cfrac{\sigma_A}{\overline{E_A}}=\cfrac{\sqrt 3} {3}=0.577$.
In this case the ratio is larger.
(e)The entropy of the system when each sudsystem is in its most probable macrostate is $$S=\ln\Omega_A(\hat E_A) \Omega_B(E_{tot}-\hat E_A)=8.8616,$$
and it is smaller than the total entropy 10.8177 caculated in part(c).
(f)
The lager the system is,the bigger the probability that energy goes from the hotter to the colder subsystem becomes,and the smaller the relative fluctuations gets.

4.7.More on tow Einstein solids in thermal contact
(a)
如果固定$N_B，E_{tot}$，改变$N_A$,则随着$N_A$增大，$S_{tot}$的最大值会发生改变，其随着$E_A$变化曲线的最大值的位置也会发生改变，$N_A$越大，最可几处的$E_A$越大；若固定$N_A，N_B$，则随着$E_{tot}$的增大，$S_{tot}$也会随着增大。

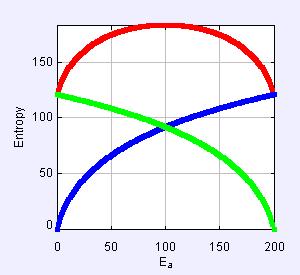
As the figure shows,if $N_A$ and $N_B$ are fixed,$S_A$ will increase as $E_A$ becomes bigger and bigger,since the bigger $E_A$ is,the bigger the number of accesible microstates of subsystem A gets.
$S_B$ is a decreasing function of $E_A$ because $E_B=E_{tot}-E_A$,when $E_A$ is a bigger value ,$E_B$ becomes a less one.
Given this dependence of $S_A$ and $S_B$ on $E_A$,$S_{tot}$ have a maximum at a particular value of $E_A$,since at this value the accesible microstats $\Omega=\Omega_A\Omega_B$ gets its maximum.
(b)
温度和曲线斜率的关系为：

$$\cfrac 1{T(E)}\approx\cfrac{S(E+\Delta E)-S(E-\Delta E)}{2\Delta E}.$$
当$N_A=N_B=50,E_{tot}=200$,如上图所示，我们可以得到：
当$E_A=100$时，$\cfrac{dS_A}{dE_A}=\cfrac{dS_B}{dE_B}$，并且此时$S_{tot}$达到最大值。
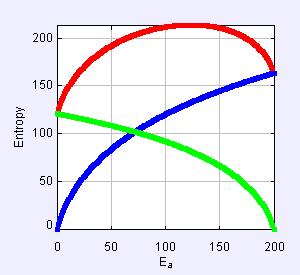改变$N_A,N_B$的值，使$N_A=80,N_B=50,E_{tot}=200$,结果如图所示：，可以得到：当$\cfrac{dS_A}{dE_A}=\cfrac{dS_B}{dE_B}$时，$S_{tot}$达到最大值。

4.8.More on Einstein solids
（a）
$E=200,N_A=N_B=4$,$P_A(E_A)$的宽度约为100;
$E=200,N_A=N_B=16$,$P_A(E_A)$的宽度约为44;
$E=200,N_A=N_B=64$,$P_A(E_A)$的宽度约为26;
可以看到，当每样粒子数各为原来粒子数的平方倍时，$P_A(E_A)$的宽度相应地变为原来的一半。
（b）
$E=20,N_A=N_B=4$,$P_A(E_A)$的宽度约为10;
$E=20,N_A=N_B=16$,$P_A(E_A)$的宽度约为7;
$E=20,N_A=N_B=64$,$P_A(E_A)$的宽度约为6;
此时没有得与（a）中相同的结论，因为此时能量太小，曲线连续性很差，估算宽度时误差太大。
（c）$P_A(E_A)$的本质是子系统A中的那个粒子能量取$E_A$的概率，曲线之所以会是$E_A$的减函数，是因为随着$E_A$增大，$E_B$减小，子系统B中的可达到的微观态数量减少，而子系统A只有一个微观态，所以总的可以达到的微观态数量减少，所以曲线为下降趋势。

4.9.Qualitative behavior of the probabilities
(a)将A和B一起考虑，系统达到某一个特定微观态的概率为1/84，现在只考虑A子系统，由Table4.3可以得到：
$E_A=6$的各微观态{（6,0），（0,6），（5,1），（1,5），（4,2），（2,4），（3,3）}达到的概率均为1/84；
$E_A=5$的各微观态{（5,0），（0,5），（4,1），（1,4），（3,2），（2,3）}达到的概率均为2/84=1/42；
$E_A=4$的各微观态{（4,0），（0,4），（3,1），（1,3），（2,2）}达到的概率均为3/84=1/26；
$E_A=3$的各微观态{（3,0），（0,3），（2,1），（1,2）}达到的概率均为4/84=1/21；
$E_A=2$各微观态{（2,0），（0,2），（1,1）}达到的概率均为5/84；
$E_A=1$的各微观态{（1,0），（0,1）}达到的概率均为6/84=1/13；
$E_A=0$的微观态（0,0）达到的概率为7/84=1/12；

（b）$N_A=4,N_B=12,E_{tot}=3$.

$E_A$	$P(E_A)$
0.0	0.44607843137254904
1.0	0.38235294117647056
2.0	0.14705882352941177
3.0	0.024509803921568627

(c)

$E_A=E_s$	$P(E_A)$	number of microstates of A	$P_s(E_s)$
0.0	0.446	1	0.446
1.0	0.3823529	4	0.096
2.0	0.1477	10	0.0147
3.0	0.0245	20	0.001125

(d)
$P_s$和$P_A(E_A)$不相等，是因为子系统A的粒子数不唯一，因为它们不是全同粒子，当给定子系统A一个特定的能量时，会在各粒子有不同的分布，造成不同的微观态，而$P_A(E_A)$还要涉及到子系统B的微观态数量，因而微观态的概率和给定能量的概率有所不同。
$P_s(E_s)$是$E_s$的单调递减函数，因为随着$E_s$的增大，A可达到的微观态的数量越来越多，子系统B会抑制子系统A的能量上升。$P_A(E_A)$随着$E_A$的变化会出现一个最大值，如果能量和粒子数比较到大，这个分布会趋近于一个高斯分布。

4.10.Rapid increase in the number of states
(a)由

$$\Omega=\cfrac{(E+N-1)!}{E!(N-1)!}\tag{7.3}$$
当$N=20$时，
$E=10,\Omega=\cfrac{(10+20-1)!}{10!(20-1)!}=20030010$
$E=10^2,\Omega=\cfrac{(10^2+20-1)!}{10^2!(20-1)!}=4.91037\times10^{21}$
$E=10^3,\Omega=\cfrac{(10^3+20-1)!}{10^3!(20-1)!}=9.928647\times10^{39}$
.....
可以看到，固定N，增大E可以使$\Omega(E)$迅速增大。
（b）考虑$E=20$,
$N=10,\Omega=\cfrac{(20+10-1)!}{20!(10-1)!}=10015005$
$N=100,\Omega=\cfrac{(20+100-1)!}{20!(100-1)!}=2.4551856\times10^{22}$
$N=1000,\Omega=\cfrac{(20+1000-1)!}{20!(1000-1)!}=4.96\times10^{41}$
......
可以看到，固定E，增大N可以使$\Omega(E)$迅速增大.

4.11.
给定一维无限深势阱中运动的粒子的能量$E=144(\cfrac{h^2}{8mL^2})$,由

$$\Gamma(E)=n=\cfrac{2L}{h}(2mE)^{1/2}$$
得到能量小于或等于E的微观态的数量为： $$n=6.$$

4.12
R较小时$\Gamma=\pi R^2/4$比精确值要大，当R增大时，$\Gamma=\pi R^2/4$不断逼近精确值，通过浏览程序运行出来的数据表可以得到如下结果，即R=118是$\Gamma=\pi R^2/4$和精确值相对误差不超过1%的最小值。

R	$\Gamma=\pi R^2/4$	微观态精确值	相对误差
117.0	10859.0	10751.31545874767	1.0015984%
118.0	11044.0	10935.88402714607	0.988635%

4.13
逼近情况和二维时类似，观察数据表可以得到结论：
R=225是$\Gamma=\pi R^2/4$和精确值相对误差不超过1%的最小值。

R	$\Gamma=\pi R^3/6$	微观态精确值	相对误差
224.0	5943946.0	5884948.644830135	1.0025%
225.0	6023512.0	5964117.303299373	0.99587%

4.14
由（4.17）能量在E和$\Delta E$之间的微观态的数量为

$$g(E)\Delta E=\Gamma(E+\Delta E)-\Gamma(E)\approx\cfrac{d\Gamma(E)}{dE}\Delta E\tag{4.17}$$
和（4.42） $$\Gamma(E)=\cfrac{4\pi}{3}\cfrac{L^3}{h^3}(2mE)^{3/2}\tag{4.42}$$
对于室温下的氮气$E=3kT/2=3/2\times1.38\times300K\times10^{-23}J/K=6.21\times10^{-20}J$
所以S室温时能量在$\Delta E=10^{-27}J$的V=1L氮气的微观态数量为 $$\begin{align} g(E)\Delta E&=\cfrac{d\Gamma(E)}{dE}\Delta E\\&=\cfrac{2\pi V}{h^3}(2m)^{3/2}E^{1/2}\Delta E\\&=\cfrac{2\pi \times 1\times10^{-3}m^3}{(6.626\times10^{-34}J·s)^3}\times\\&(2\times(14.0037\times1.66053886\times10^{-27}kg))^{3/2}\\&\times(6.21\times10^{-20}J)^{1/2}\times10^{-27}J\\&=5.398\times10^{25}. \end{align}$$

4.15.Approximate expression for $\Gamma(E,V,N)$
对于三维无限深势阱里的单粒子有能量小于或等于E的微观态数量为$\Gamma(E)=\cfrac{4\pi}{3}\cfrac{V}{h^3}(2mE)^{3/2}$,考虑N个无相互作用粒子，有

$$\begin{align}\Gamma(E,V,N)&=\cfrac 1{N!}\Gamma_1(\cfrac{E}{N},V)^N\\&=\cfrac 1{N!}(\cfrac{4\pi}{3})^N(\cfrac{V}{h^3})^N(2m\cfrac EN)^{3N/2}. \end{align}$$
在这种简单考虑下$\Gamma(E,V,N)$和$E^{3N/2},V^N$成正比（当N固定）；这和4.49式给出的是相同的。

4.16.Density of statesof an ideal gas

$$\Gamma(E,V,N)=\cfrac{1}{N!}(\cfrac{V}{h^3})^N\cfrac{(2\pi mE)^{3N/2}}{(3N/2)!}$$
$$\ln \Gamma(E,V,N)=N\ln{\cfrac{V}{N}}+\cfrac 32 N\ln{\cfrac{mE}{3N\pi \hbar^2}}+\cfrac 52N$$
$$\begin{align}g(E,V,N)&=\cfrac{d\Gamma}{dE}\\&=\Gamma(E,V,N)\cfrac{d\ln{\Gamma}}{dE}\\&=\cfrac{1}{N!}(\cfrac{V}{h^3})^N\cfrac{(2\pi m)^{3N/2}E^{3N/2-1}}{(3N/2-1)!} \end{align}$$
因为$\cfrac{d\ln{\Gamma}(E,V,N)}{dE}=\cfrac{3N}{2E}>0$,所以$\Gamma(E,V,N)$是E的递增函数，且增长速度很快；
$\cfrac{d\ln{\Gamma}(E,V,N)}{dV}=\cfrac{V}{N}>0$,所以$\Gamma(E,V,N)$是V的递增函数，且增长速度很快；
$\cfrac{d\ln{\Gamma}(E,V,N)}{dN}=-\cfrac{5}{2}\ln N<0$,所以$\Gamma(E,V,N)$是N的递减函数；
$\begin{align} \ln g(E,V,N)&=\ln{\Gamma(E,V,N)}+\ln{\cfrac{3N}{2E}} \\&=N\ln{\cfrac{V}{N}}+\cfrac 32 N\ln{\cfrac{mE}{3N\pi \hbar^2}}\\&+\cfrac 52N+\ln{\cfrac{3N}{2E}} \end{align}$
所以$\cfrac{d\ln g(E,V,N)}{dE}=\cfrac{3N-2}{2E}>0$,所以$g(E,V,N)$是E快速递增函数；
$\cfrac{d\ln g(E,V,N)}{dV}=\cfrac{N}{V}>0$,所以$g(E,V,N)$是V快速递增函数；
$\cfrac{d\ln g(E,V,N)}{dN}=\cfrac{1}{N}-\cfrac{5}{2}\ln N<0$,所以$g(E,V,N)$是N递减函数.

4.17
式4.63中有

$$S(E,V,N)=Nk[\ln{\cfrac VN}+\cfrac 32\ln{\cfrac{mE}{3N\pi \hbar^2}}+\cfrac 52]\tag{4.63}$$
考虑$N\to \infty,$所以有 $$dS=Nk(\cfrac{dV}{V}+\cfrac 32 \cfrac{dE}{E}),$$
此式即为2.19节中的式（2.131）式，可见（4.63）中的熵的形式与热学中的定义相符。

4.18
由定义

$$S=k\ln g(E)\Delta E\tag{4.62a}$$
又有 $$\begin{align}\ln g(E)\Delta E&=\ln g(E)+\ln\Delta E\\&=\ln \Gamma(E)+\cfrac{3N}{2E}+\ln\Delta E\\&=\ln \Gamma(E)+\ln\cfrac{3N\Delta E}{2E} \end{align}$$
因为$N\to \infty,\cfrac{\Delta E}{E}\to 0$,所以$\ln\cfrac{3N\Delta E}{2E}\approx 0.$
即（6.62a)和（6.62b）可以近似等效。
由 $$\ln \Gamma(E,V,N)=N\ln{\cfrac{V}{N}}+\cfrac 32 N\ln{\cfrac{mE}{3N\pi \hbar^2}}+\cfrac 52N$$
所以 $$\begin{align} S(E,V,N)&=k\ln g(E)\Delta E\\&=Nk[\ln{\cfrac VN}+\cfrac 32\ln{\cfrac{mE}{3N\pi \hbar^2}}+\cfrac 52].\tag{4.63} \end{align}$$

4.19
由$E=\cfrac 32 NkT\to \cfrac EN=\cfrac 32kT,$将之带入（6.63）可得：

$$\begin{align} S(E,V,N)&=k\ln g(E)\Delta E\\&=Nk[\ln{\cfrac VN}+\cfrac 32\ln{\cfrac{mE}{3N\pi \hbar^2}}+\cfrac 52]\\&=Nk[\ln{\cfrac VN}+\cfrac 32\ln{\cfrac{mkT}{2\pi \hbar^2}}+\cfrac 52]. \end{align}$$

4.20
由

$$\cfrac{\mu}{T}=-(\cfrac{\partial S}{\partial N})_{E,V}$$
得到 $$\begin{align} \mu&=-T(\cfrac{\partial S}{\partial N})_{E,V}\\&=\cfrac{5}{2}kTN\ln N \end{align}$$
又有$E=\cfrac 32 NkT\to T=\cfrac 23\cfrac{E}{Nk},$所以
$$\begin{align} \mu&=\cfrac{5}{2}kTN\ln N\\&=\cfrac 53E\ln N. \end{align}$$

4.21
由

$$\cfrac 1T=-k\cfrac 1{2\mu B}\ln{\cfrac{N-n}{n}}\tag{4.72}$$
得到 $$\cfrac{2\mu B}{kT}=\ln{\cfrac{n/N}{1-n/N}}$$
得到 $$e^{\frac{2\mu B}{kT}}=\cfrac{n/N}{1-n/N}$$
所以 $$\begin{align} p=\cfrac nN&=\cfrac 1{1+e^{-\frac{2\mu B}{kT}}}\\&=\cfrac{e^{\mu B/kT}}{e^{-\mu B/kT}+e^{\mu B/kT}}\\&=\cfrac{e^{\beta\mu B}}{e^{-\beta\mu B}+e^{\beta\mu B}}.\tag{4.74} \end{align}$$
把上式代入$E=-(2n-N)\mu B$得 $$\begin{align} E&=-(2\cfrac{Ne^{\beta\mu B}}{e^{-\beta\mu B}+e^{\beta\mu B}}-N)\mu B\\&=-N\mu B\cfrac{e^{\beta\mu B}-e^{-\beta\mu B}}{e^{-\beta\mu B}+e^{\beta\mu B}}\\&=-N\mu B \tanh{\beta \mu B}.\tag{4.73} \end{align}$$
其中$\beta=1/kT.$

4.22
这些一维谐振子满足爱因斯坦固体模型，所以N个谐振子可达到的微观态的数量为

$$\Omega=\cfrac{(Q+N-1)!}{Q!(N-1)!}$$
所以 $$S=k\ln\Omega=\ln(Q+N-1)!-\ln Q!-\ln(N-1)!$$
$$\cfrac{dS}{dQ}=k\ln(Q+N-1)-k\ln Q$$
又由$E=(Q+\cfrac 12 N)\hbar w \implies Q=\cfrac{E}{\hbar w}-\cfrac 12 N \implies \cfrac{dQ}{dE}=\cfrac{1}{\hbar w}$
所以 $$\begin{align}\cfrac 1T=(\cfrac{\partial S}{\partial E})_{V,N}&=\cfrac{dS}{dQ}\cfrac{dQ}{dE}\\&=\cfrac{1}{\hbar w}[k\ln(Q+N-1)-k\ln Q]\\&=\cfrac{k}{\hbar w}\ln[1+(N-1)\cfrac{\hbar w}{E}]. \end{align}$$
所以 $$E(T)=\cfrac{(N-1)\hbar w}{e^{\hbar w/kT}-1}.$$

4.23
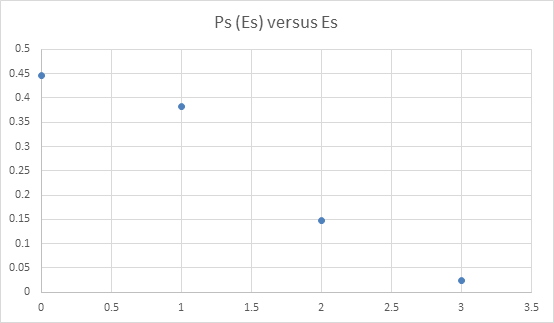
从表格4.6中我们总结出Ps是Es的单调递减函数，现在分析波尔兹曼分布

$$P_s=\cfrac 1Z e^{-\beta E_s}\tag{4.79}$$
它是系统和恒温热源达到热力学平衡时微观态s的概率，它也是一个递减函数。
而表格4.6中的子系统B不是恒温热源，但其和A组成的组合系统达到微观态S的概率依旧为减函数。
这两种情况有一个共同点，那就是我们研究的都是一个很小的系统和与之相比很大的系统，以至于感兴趣的系统的微观态数量仅为1，所以当它的微观态的能量高时，另外的那个子系统的能量降低，导致系统的总微观态数量降低，随着Es的增大呈递减函数。

4.24
假设这是一个两个同分异构体的多个粒子组成的组合系统，并假设其中有n个trans-2丁烯，N-n个cis-2丁烯，系统总能量为$E=n\Delta E+NE_{trans-2}$
得到$\cfrac{dn}{dE}=\cfrac{1}{\Delta E},$
系统总微观态数量为

$$\Omega=\cfrac{N!}{n!(N-n)!}$$
所以$S=k\ln \Omega$,得到 $$\cfrac{dS(n)}{dn}=k[-\ln n+\ln(N-n)],$$
$$\begin{align}\cfrac 1T=(\cfrac{\partial S}{\partial E})_{V,N}&=\cfrac{dS}{dn}\cfrac{dn}{dE}\\&=\cfrac{k}{\Delta E}\ln\cfrac{N-n}{n}\end{align}$$
所以得到系统中有n个trans-2丁烯的概率为 $$p=\cfrac nN=\cfrac{1}{1+e^{\Delta E/kT}}$$
相对丰度为 $$\cfrac{N-n}{n}=e^{\Delta E/kT}$$
T=300K时 $$\cfrac{N-n}{n}=e^{\Delta E/kT}=e^{4180/300}=1125044.7080,$$
T=1000K时 $$\cfrac{N-n}{n}=e^{\Delta E/kT}=e^{4180/1000}=65.366.$$

4.25

4.26

4.27
T=0的基态下，在没有外加磁场的情况下，一个电子自旋仍有两种取向，概率相同，对于N个电子，总共有$2^N$种配置的方式，即微观态的数量为$\Omega=2^N$,所以系统的熵为$S=k\ln\Omega=kN\ln2.$

4.28
(a)在例4.3中得到一个一维谐振子的配分函数为$Z_1=\cfrac{e^{-\beta \hbar w/2}}{1-e^{-\beta \hbar w}}, \ln Z_1=-\cfrac 12 \beta \hbar w-\ln(1-e^{-\beta \hbar w}),$
所以

$$f=-kT\ln Z_1=\cfrac 12\hbar w+kT\ln(1-e^{-\beta \hbar w})$$
$$\bar e=-\cfrac{\partial}{\partial \beta}\ln Z_1=\hbar w[\cfrac 12+\cfrac{1}{e^{\beta \hbar w}-1}]\tag{4.132}$$
所以 $$s=\cfrac{e-f}{T}=\cfrac{\hbar w}{T(e^{\beta \hbar w}-1)}-k\ln(1-e^{-\beta \hbar w})\\=k[\cfrac{\beta\hbar w}{e^{\beta \hbar w}-1}-\ln(1-e^{-\beta \hbar w})].$$
(b)
给定4.132式，则N个谐振子和温度为T的热缸达到热力学平衡时的平均能量为 $$\overline E =N\bar e=N\hbar w[\cfrac 12+\cfrac{1}{e^{\beta \hbar w}-1}].$$
(c)
在4.22中得到 $$E(T)=\cfrac{(N-1)\hbar w}{e^{\hbar w/kT}-1}，$$
这和在正则系综中得到的结果并不一样。

5.1
(a)
由式5.6知正则系综下$\overline E=-N\mu B\tanh{\beta \mu B},$在问题4.21中得到在微正则系综下的能量为$E==-N\mu B \tanh{\beta \mu B}.$可见二者是相等的。
(b)
因为在正则系综情况下，我们可以先考虑一个粒子的情况，N个粒子的情况只需要对一个粒子时的情况重复N次，而微正则系综需要同时考虑N个粒子的情况，计算时微观态的数量比较庞大。
(c)
正则系综下，由$Z_1=e^{\beta \mu B}+e^{-\beta \mu B}$,自旋和外磁场平行的概率为$p=\cfrac{e^{\beta \mu B}}{e^{\beta \mu B}+e^{-\beta \mu B}}.$这和微正则系综时给出的结果一样。
(d)
两种情况得出的结果一样。

5.2
由$\begin{align} \overline M&=\cfrac 1Z\sum_s M_se^{-\beta(E_{0,s}-M_{s}B)}\tag{5.15a}\\&=\cfrac 1{\beta Z}\cfrac{\partial Z}{\partial B}\tag{5.15b} \end{align}$
且

$$\cfrac{\partial^2Z}{\partial B^2}=\sum_s \beta^2M_s^2e^{-\beta(E_{0,s}-M_{s}B)}=\beta^2\overline{M^2}Z$$
所以 $$\begin{align}\chi=\cfrac{\partial M}{\partial B}&=\cfrac{\partial }{\partial B}(\cfrac 1{\beta Z})\cfrac{\partial Z}{\partial B}+\cfrac 1{\beta Z}\cfrac{\partial^2 Z}{\partial B^2}\\&=\cfrac 1{\beta}(-\cfrac 1{\beta Z^2})(\cfrac{\partial Z}{\partial B})^2+\cfrac 1{\beta Z}\cfrac{\partial^2 Z}{\partial B^2}\\&=-\beta \overline M^2+\beta \overline{M^2}\\&=\cfrac 1{kT}[\overline{M^2}-\overline M^2]. \end{align}$$

5.3
(c)
对于N个无相互作用的自旋，其能量平均值和亥姆霍兹自由能均已求出，分别为

$$\overline E=-N\mu B\tanh \beta \mu B$$
$$F=-NkT\ln (2\cosh\beta \mu B)$$
所以熵为 $$S=\cfrac{\overline E-F}{T}=Nk\ln (2\cosh\beta \mu B)-\cfrac{N\mu B}T\tanh \beta \mu B$$
当$kT<<\mu B$时，$S\to 0$;
当$kT>>\mu B$时，$S\to 0$.
S以来于$kT$和$\mu B$的比值。
5.4
(a)
75%的原子自旋朝上，则系统的平均能量为$\overline E=0.75N(-\mu B)+0.25N\mu B=-\cfrac N2 \mu B.$
和一个热缸达到热力学平衡时属于正则系综的情况，此时的配分函数已由前面求得，$Z_N=(2\cosh \beta \mu B)^N$,系统的平均能量为$\overline E =-N\mu B\tanh \beta \mu B.$
所以有 $$-N\mu B\tanh \beta \mu B=-\cfrac N2 \mu B$$
解得 $$T=\cfrac{\mu B}{k\ln3}=2.446K.$$
(b)
由$E=E_0-MB$,则 $$dE=-d(MB)$$ 因为是B的准静态改变，所以 $$d(MB)=MdB$$
$$\begin{align} \Delta E&=-\int_1^{10}N\mu B\tanh(\beta \mu B)dB\\&=-NkT\ln(2\cosh \beta \mu B)|_1^{10}\\&\approx-8.027. \end{align}$$
(c)
绝热过程，系统总能量不会改变，即在B=10T和B=1T时系统具有相同的能量，所以有 $$\overline E(B_1=10)=-N\mu B_1\tanh \beta_1 \mu B_1=\\\overline E(B_2=1)=-N\mu B_2\tanh \beta_2 \mu B_2$$
解得 $$T_2=$$