期末作业——Ising model

材料班 郭忠智 2014301020087

---

1 前言

在本文中展示了用蒙特卡洛方法去对正则系综下的$10\times10$格点的伊辛模型进行模拟，给出模拟得到的结果，其包括平均分子磁矩，平均分子能量，有外场作用下分子磁矩随外磁场强度的变化情况。

2 背景

伊辛模型(Ising model)多粒子系统中具有代表性的模型，它用来处理一个由有相互作用多个自旋子构成的多粒子系统，其中每个自旋的位置被固定在一个格点上，每个自旋和它最相邻的自旋之间有相互作用。

3 正文

3.1 原理

考虑在二维平面内的位置固定于$10\times10$格点上的自旋，其相互之间有相互作用，我们只考虑最邻近的自旋之间的相互作用以及每个自旋和外磁场之间的相互作用，对于某一个自旋，其自旋方向有两种情况，即朝上和朝下。整个系统的能量由下式表出：

$$E=J\sum_{<ij>}s_is_j-\mu H\sum_i s_i\tag{1}$$
其中，$J$为交换常数，表示两个粒子的相互作用能的大小，$\mu$为自旋的磁动量，$H$为外加磁场强度，$s_i、s_j$表示第i个粒子和第j个粒子的自旋的大小，在这里我们假设：
$$s_i=\begin{cases}1,自旋朝上\\-1, 自旋朝下\end{cases}$$

对于N个自旋，在温度为T时的磁化强度为：

$$M=\sum_i<s_i>=N<s_i>\tag{2}$$
此处考虑理想化情况：假设系统无限大，我们考虑的系统离边界很远，于是我们忽略边界效应系统中每个粒子的平均自旋相等。
假设没有外场作用，则系统的能量为： $$E=-J\sum_{<ij>}s_is_j=-\left(J\sum_{<ij>}s_j\right)s_i\tag{3}$$
将括号中的因子视为一个等效的外场： $$\mu H_{eff}=J\sum_{<ij>}s_j\tag{4}$$
记离一个自旋最近的自旋数量为z，则有：
$$H_{eff}=\cfrac{J}{\mu}\sum s_j=\cfrac{zJ}{\mu}<s>\tag{5}$$
在正则系综下，微观态的分布遵循波尔兹曼分布， 考虑系统中的某一自旋$s_i$，其取值如(2)式所述，其平均值为：
$$<s_i>=\sum_{s_i=\pm1}s_i P_{\pm}=P_{+}-P_{-}=\tanh (\mu H/k_B T)\tag{6}$$
将（5）式代入（6）中得到：
$$<s>=\tanh(zJ<s>/k_B T)\tag{7}$$
这个方程描述了在温度T下系统的平均自旋，对应不同的温度，每个粒子的平均自旋有不同的取值。
但是(7)式是一个超越方程，一般情况其没有解析解，只能用模拟进行求解。

3.2 蒙特卡洛方法模拟

蒙特卡洛方法用随机方法，模拟系统中的自旋子和外界热源交换的能量。
(1) 选择一个自旋，假设其原先的能量为E，可由（1）式计算得到，计算其反转所需要的能量：

$$E_{flip}=-2E$$
(2) 当$E_{flip}<0$，反转自旋；
当$E_{flip}>0$，将波尔兹曼因子$\exp(-E_{flip}/k_BT)$与一个在0和1之间均匀分布的随机数比较，如果波尔兹曼因子比随机数大，将自旋反转，反之则让自旋保持原状态。

3.3 蒙特卡洛方法的有效性

蒙特卡洛自旋反转联系着两个状态：记为$1，2$，并假设它们的能量满足$E_1>E_2$.如果系统处于态1，在一个蒙特卡洛步中从态1转变到态2的速率为$E_1>E_2$，并且因为$E_1>E_2$，所以$W(1\to2)=1$，因为这样使系统能量更低；如果系统处于态2，则其转变到态1的速率为$W(1\to2)=\exp[-(E_1-E_2)/k_BT]$。
转变状态的粒子数和转变速率与粒子处在的微观态的概率$P_i$的乘积成正比，如果将两种转变的数量相等，意味着系统和热源达到热力学平衡：

$$P_1W(1\to2)=P_2W(2\to1)$$
得到： $$\cfrac{P_1}{P_2}=\exp[-(E_1-E_2)/k_BT]$$
即粒子在某个态的概率遵循波尔兹曼分布，这和统计物理给出的结果相符合，所以用蒙特卡洛方法模拟是正确的。

3.4 程序模拟

考虑二维平面，$10\times10$的格点，以及周期性边界条件。

3.4.1 无外场作用的情况

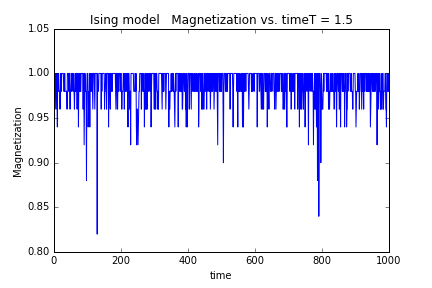
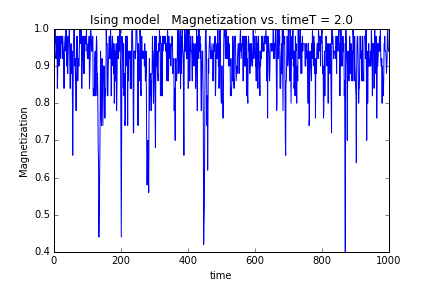
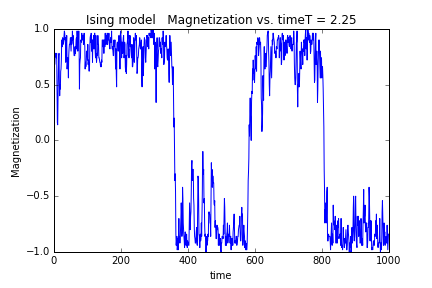
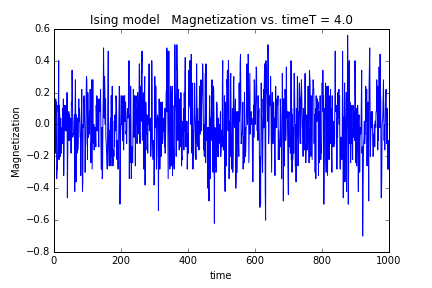
（1）模拟热接触，从初态达到平衡态，观察不同wen平均磁矩随时间的变化
代码
结果如图：

（2） 各个热力学量随温度的变化关系
以下是模拟中各个热力学量的计算
能量随温度的变化：

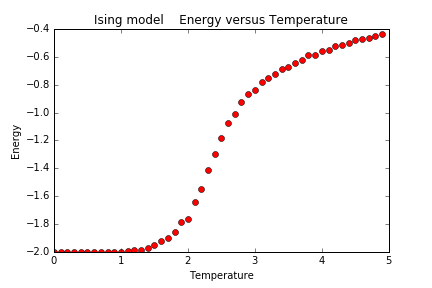
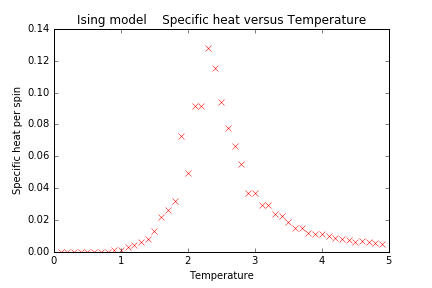
热容随温度的变化：

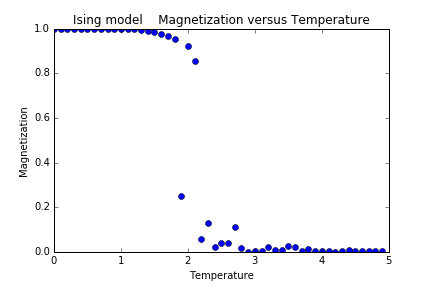
平均磁矩随温度的变化：

磁化率随温度的变化：

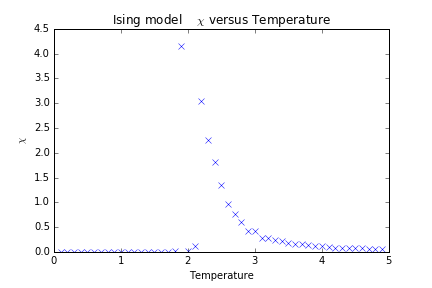
从以上四个热力学量随温度的变化情况来看，在T=2.25附近确实发生了相变，这种相变是二级相变。

3.4.2 有外磁场作用的情况

当外场不为零时，观察特定温度下，磁矩随磁场强度的变化情况：

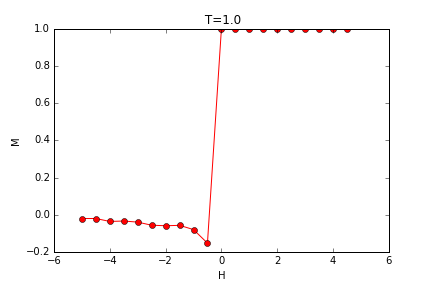
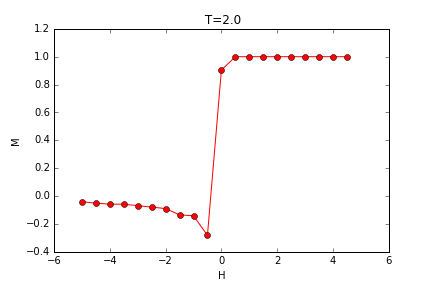
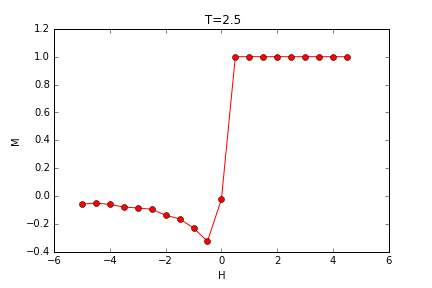
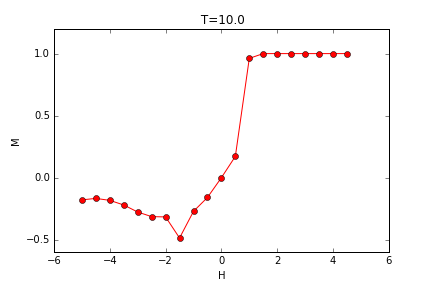
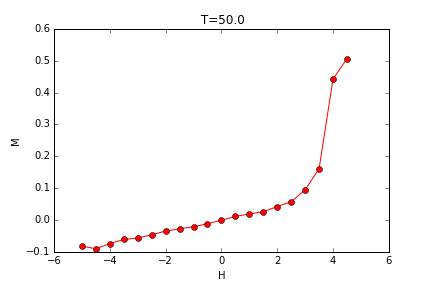
可以观察到，在低温时，外场从变化方向时对应着大量自旋的反转，发生相变，此时对应的是一级相变，而当温度增大，磁矩的变化变得连续，需要更大的外磁场才能引发相变。

3.5 代码

作业代码 Ising model

4 结论

通过用蒙特卡洛方法对伊辛模型进行模拟，得到了有关相变的各个热力学量包括能量，磁化强度，热容，磁化率等，从这些热力学量随温度的变化关系可以知道，当无外磁场作用时，在某个特定温度下会发生相变，这种相变就是顺磁相变，它是一种二级相变；而当有外磁场作用时，当磁场变化方向时，系统热会发生相变，只不过此时对应的是一种一级相变，温度的作用变得更小了，而在高温时，温度和外磁场的共同作用使得相变又发生了变化，使磁化强度的变化变得连续，而非之前的突然跳变。

5 致谢

参考书目：Computational Physics, Nicholas J. Giordano & Hisao Nakanishi