第十三次作业

计算物理 郭忠智2014301020087

---

1 摘要

本次作业完成了第六章两端固定的弦的波动问题，在先假设弦的振动没有耗散以及弦是理想的，不受材料性质的约束的情况下，进一步加入了因为材料引起的僵硬的弦（非理想情况），给其一个打击使其发生振动，画图研究波在弦上的传播情况，以及在某一固定点的振动情况及其能谱。

2 背景

Problem6.16
Perform the caculations described in this section.

正文

（1）理想情况
波动方程为：

$$\cfrac{\partial^2 y}{\partial t^2}=c^2 \cfrac{\partial^2 y}{\partial x^2}\tag{1}$$
对波动的弦坐划分，考虑其中的某一小段，受力分析有,由牛顿第二定律：
$$(\mu \Delta x)\cfrac{\partial^2 y_i}{\partial t^2}=T\sin\theta_{i+1}-T\sin\theta_{i}$$
其中$\theta_i$是第i段微元受到其左边的微元的作用力与水平方向的夹角。
在位置为$x_i$处的微元离开平衡位置的距离为$y_i$,则有：
$$\sin\theta_i\approx\cfrac{y_i-y_{i-1}}{\Delta x}$$
然后得到： $$\cfrac{d^2 y_i}{d t^2}\approx(\cfrac T{\mu} )\cfrac{y_{i+1}-2y_i+y_{i-1}}{(\Delta x)^2}$$
令$x=i\Delta x, t=n\Delta t$
得到： $$y(i,n+1)=2[1-r^2]y(i,n)-y(i,n-1)\\+r^2[y(i+1,n)+y(i-1,n)]\tag{2}$$
(2)考虑材料的僵硬带来的影响
这个影响因子在波动方程里是一个四阶偏导数的项，此时波动方程写为：
$$\cfrac{\partial^2 y}{\partial t^2}=c^2( \cfrac{\partial^2 y}{\partial x^2}-\epsilon L^2)\cfrac{\partial^4 y}{\partial x^4}\tag{3}$$
根据导数的定义，最后可得到：
$$y(i,n+1)=2[1-r^2-3\epsilon r^2M^2]y(i,n)-y(i,n-1)\\+r^2[1+4\epsilon M^2][y(i+1,n)+y(i-1,n)]\\-\epsilon r^2 M^2[y(i+2,n)+y(i-2,n)]\tag{4}$$
在(2)(4)两式中，$r=c\Delta t/\Delta x,M=L/\Delta x$,L为弦的长度。
（3）初始条件和边界条件
初始条件，给定一个高斯分布的波形去扰动弦：
$$y_0(x)=\exp[-k(x-x_0)^2]$$
其中x属于[0,1]，$k=1000m^{-2}$
边界条件为$y(0,n)=y(M,n)=0$.

程序代码如下：
Fixed string

运行程序的结果：
理想情况在左边，考虑材料硬度的影响后的结果在右边



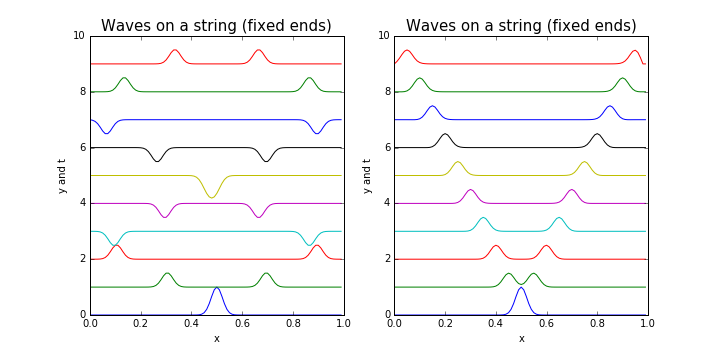
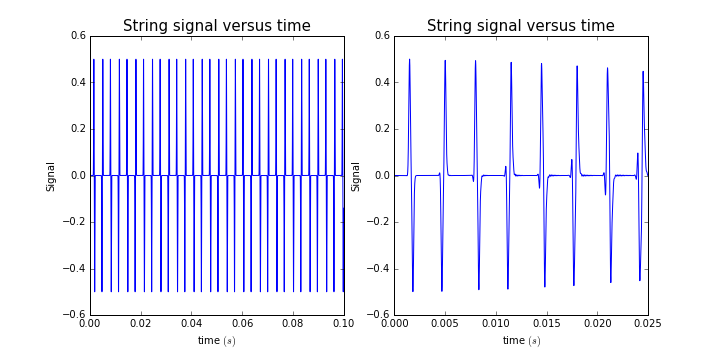
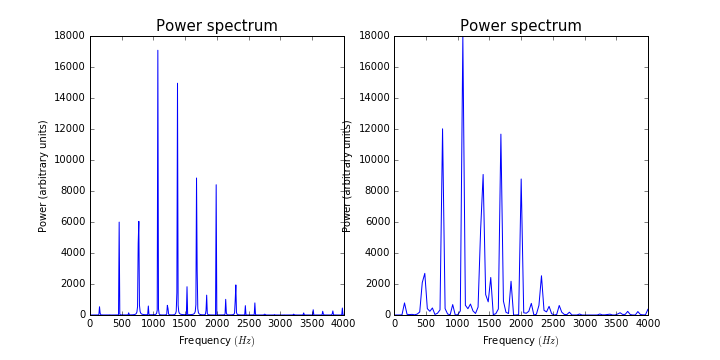
当取不同的$\epsilon$的值时，其能谱有一定的差别：

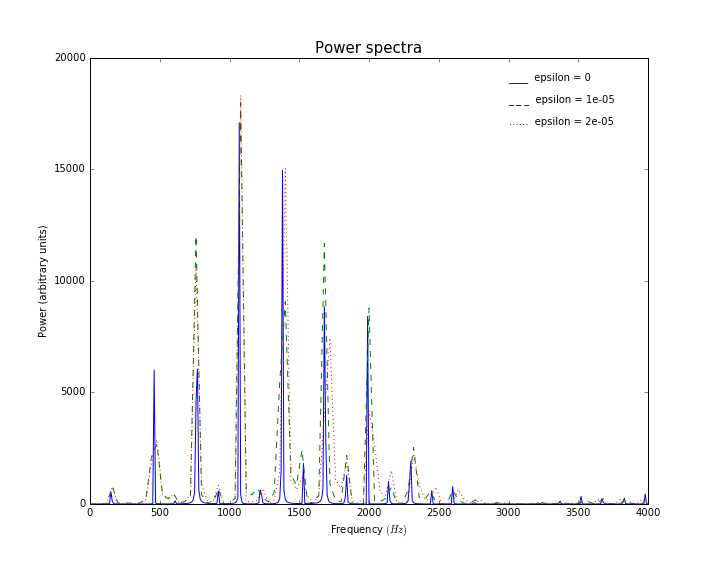
4 结论

通过计算，画图，可以看到考虑实际的材料的影响后，弦的振动变得不一样了，波形，每个弦上的点的运动，伯德能谱均会发生变化。

5 致谢

参考资料：computational physics by Nicholas J.Giordano,Hisao Nakanishi.