第六次作业 chapter2 exercise2.9

朱楚楚 材料物理 2013301510058
computationalphysics chapter2

---

摘要

抛体运动问题；最大发射角度；空气阻力（随高度变化）；欧拉法；

背景

　　本文以炮弹为例讨论抛体运动中蕴含的物理问题。
　　不考虑空气阻力对物体的影响时，抛体运动方程可分解成两个垂直方向的二阶常微分方程，求解简单。理想情况下最大发射角度为$45^\circ$。
　　考虑空气阻力并进一步认为空气密度会随高度变化时，抛体运动问题变得十分复杂、不易求精确解，本文从欧拉方法出发对各种考虑下的抛体运动问题进行求解，用图像进行分析并给出实际情况下的最大发射角度。

正文

在所有的考虑情况中，$初始速度v_0=700m/s，重力加速度g=9.8m/s$。

不考虑空气阻力

• 物体沿竖直$y$方向受到重力$mg$，沿水平$x$方向不受力。设$发射角度为\theta$，为根据牛顿第二定律：
  $$v_{x0}=v_0cos\theta$$
  $$v_{y0}=v_0sin\theta$$
  $$\frac{d^2x}{dt^2}=0$$
  $$\frac{d^2y}{dt^2}=g$$
  直接解得水平方向射程为：
  $$x=\frac{2v_0cos\theta sin\theta}{g}=\frac{v_0sin2\theta}{g}$$
  炮弹飞过的水平距离与初始的发射角度有关。
  　　将上述式子都写成有限的微分形式：
  $$\begin{cases}x_{i+1}=x_i+v_{x,i}\Delta t\\ v_{x,i+1}=v_{x,i}\\ y_{i+1}=y_i+v_{y,i}\Delta t\\ v_{y,i+1}=v_{y,i}-g\Delta t\end{cases}$$
  选择角度分别为$30^\circ,35^\circ,40^\circ,45^\circ,50^\circ,55^\circ$，运用欧拉法求出数值解，并用图像给出了不同发射角度下炮弹的运动轨迹：
  
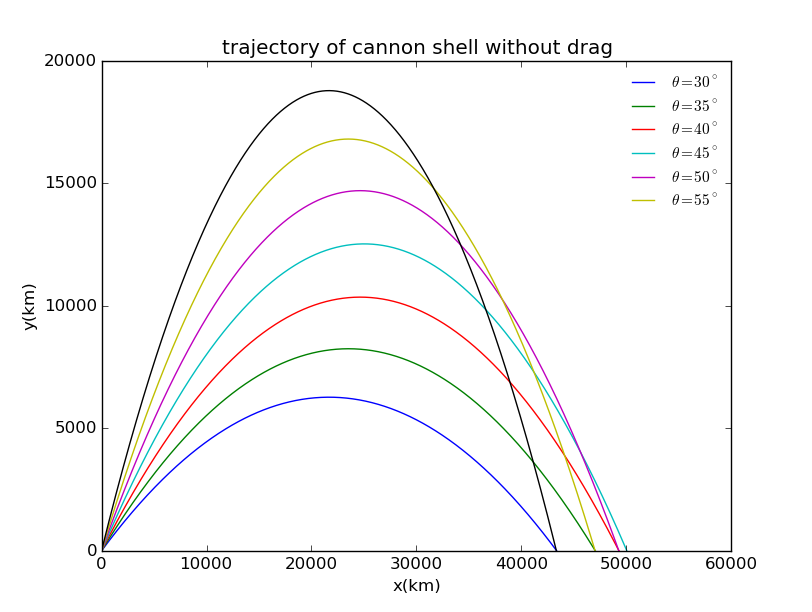
  从图像及精确解都可以得到结论如下：
  （1）角度为45度时射程最远；
  （2）角度和为90度的两种炮弹射程相同但最大高度不同。

考虑空气阻力但不考虑空气密度随高度变化　　

　　空气阻力随速度的变化关系由下给出：

$$F_{drag}=-B_2v^2（忽略一阶项）$$
$$F_{drag,x}=F_{drag}cos\theta=F_{drag}(v_x/v)=-B_2\,v\,v_x$$
$$F_{drag,y}=F_{drag}sin\theta=F_{drag}(v_y/v)=-B_2\,v\,v_y$$
增加空气阻力之后炮弹运动方程可写为：
$$\begin{cases}x_{i+1}=x_i+v_{x,i}\Delta t\\ v_{x,i+1}=v_{x,i}-\frac{B_2\,v\,v_{x,i}}{m}\Delta t\\ y_{i+1}=y_i+v_{y,i}\Delta t\\ v_{y,i+1}=v_{y,i}-g\Delta t-\frac{B_2\,v\,v_{y,i}}{m}\Delta t\end{cases}$$

　　设$\frac{B_2}{m}=1\times10^{-5}\;m^{-1}$，发射角度为$drag\theta$，选择角度为$drag\theta$=$30^\circ$，$35^\circ$，$40^\circ$，$45^\circ$，$50^\circ$，$55^\circ$，运用欧拉法求出数值解，画图显示炮弹的运动轨迹并与无阻力时炮弹的运动轨迹进行比较：

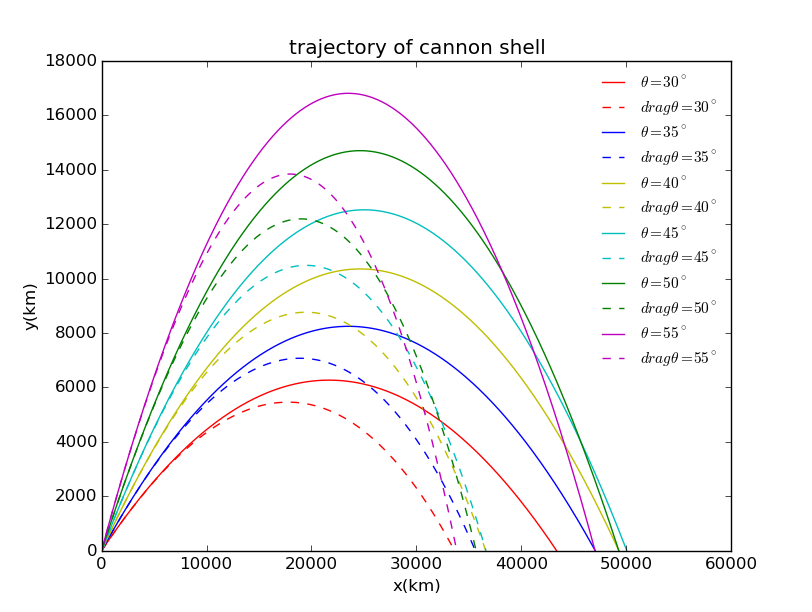
从图像上可以得到结论如下：
（1）阻力因素在炮弹的发射中起着很重要的作用。同样角度下考虑阻力时炮弹的射程和能达到的最大高度远远小于不考虑阻力时炮弹的射程和最大高度；
（2）考虑阻力时，“角度和为90度的两种炮弹射程相同”这种说法不再成立；
（3）考虑阻力后的炮弹运动轨迹依然是抛物线。
代码在此

　　$入射角度固定为\theta=45^\circ$，选择不同的空气阻力系数$\frac{B2}{m}，$画图显示炮弹的运动轨迹进行比较：

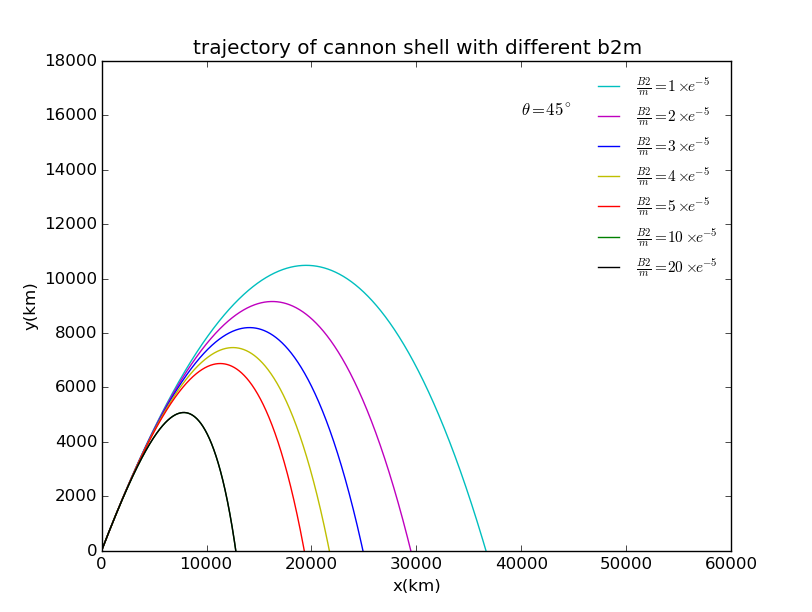
从图像上可以得出符合预期的结论：空气阻力系数越大，炮弹的射程和最大高度越小。
代码在此

考虑空气阻力同时考虑空气密度随高度发生变化

　　通过以上两个图像可以看出空气阻力在抛体运动中起到了十分重要的作用，但这个简单模型中忽视了一个重要因素。从图中可以看出，炮弹运动高度变化范围很大（0～12000km），高度对空气密度的影响不能忽略，随着高度的增加空气密度逐渐降低，空气阻力也会随之减小。换句话说，空气阻力不是固定值而是高度的函数。

$$\rho=\rho(y),F_{drag}=F_{drag}(y)=\frac{\rho}{\rho_0}F_{drag}(0)=-\frac{\rho}{\rho_0}B_2v^2$$ 为了考虑空气阻力随高度变化对炮弹轨迹的影响，即求$\frac{\rho}{\rho_0}$。近似认为空气是理想气体，引入等温模型和绝热模型。

等温模型

　　对于近似为理想气体等温模型的空气，压强随高度的变化如下：

$$p(y)=p(0)e^{-\frac{mgy}{k_BT}}$$
$m$是单个空气分子的平均质量，$k_B$是玻尔兹曼常数，$y$是距离参考点（水平面）的高度,$T$是绝对温度，$\rho_0$是海平面(y=0)的空气密度。对于理想气体，压强和密度成正比，因此：
$$\rho=\rho_0exp(-y/y_0)$$
$y_0=\frac{k_BT}{mg} \approx 1.0\times10^4m$，$\rho_0$是海平面(y=0)的空气密度。因此运动方程可化为：
$$\begin{cases}v_{x,i+1}=v_{x,i}-e^{\frac{-y}{y_0}}\cdot\frac{B_2\,v\,v_{x,i}}{m}\Delta t\\ v_{y,i+1}=v_{y,i}-g\Delta t-e^{\frac{-y}{y_0}}\cdot\frac{B_2\,v\,v_{y,i}}{m}\Delta t\end{cases}$$

绝热模型

$$\rho=\rho_0(1-\frac{ay}{T_0})^\alpha$$
$a\approx6.5\times10^{-3}K/m,T_0是海平面的开尔文温度，对空气而言\alpha\approx2.5。$因此运动方程可化为：
$$\begin{cases}v_{x,i+1}=v_{x,i}-(1-\frac{ay}{T_0})^\alpha\cdot\frac{B_2\,v\,v_{x,i}}{m}\Delta t\\ v_{y,i+1}=v_{y,i}-g\Delta t-(1-\frac{ay}{T_0})^\alpha\cdot\frac{B_2\,v\,v_{y,i}}{m}\Delta t\end{cases}$$
　　固定入射角为$\theta=45^\circ$，比较等温模型、绝热模型与不考虑随高度变化的空气阻力及不考虑空气阻力时的炮弹轨迹，图像如下：

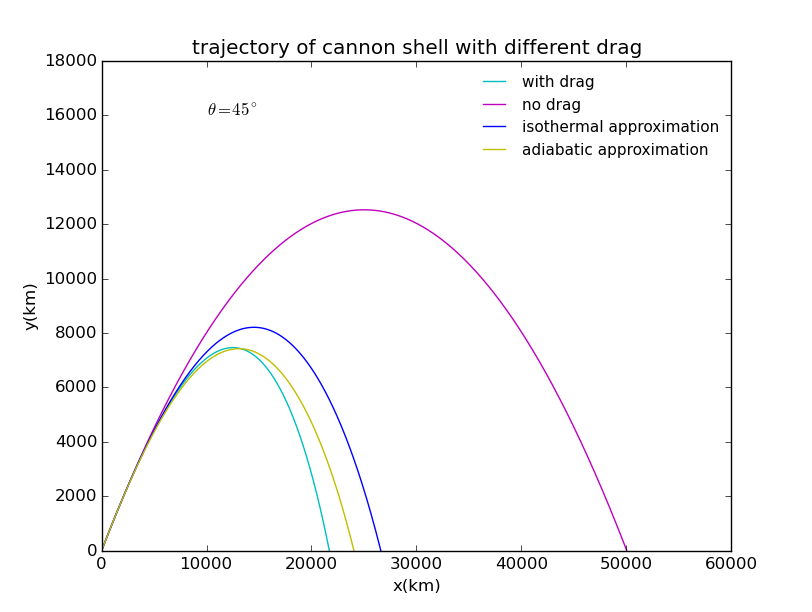
从图像上可以得出结论：
（1）四种考虑情况下炮弹的运动轨迹均为抛物线；
（2）不管是等温模型还是绝热模型都可以看出，当高度$y$变化时，空气密度呈指数函数下降，这说明当$y$变化范围很大时，空气密度是一个不可忽略的影响因素。
代码在此

结论

见上

致谢

[1] 【python】matplotlib.pyplot入门，作者Jason Ding
[2] 蔡浩老师的例子及刘星辰、陈洋遥、李芳莹、岳绍圣同学的作业
[3] 计算物理课本
[4] markdown说明