第十次作业 chapter3 exercise3.26

朱楚楚 材料物理 2013301510058
computationalphysics chapter3

---

摘要

流体问题；混沌现象；Lorenz模型；

背景

　　在chapter3中我们已经考虑了单摆运动和周期加倍两种简单系统，至此它们展现出非常丰富的行为。不可否认还有别的更加复杂的系统中也存在混沌现象，而我们首先能想到的具有这种性质的系统就是天气了。为了从更基础的角度来理解天气问题，大气科学家E.N.Lorentz从描述粘性不可压缩流体动量守恒的运动方程——Navier-Stokes方程出发，在rayleigh-benard问题下对其进行简化得到Lorenz模型，方程式如下：

$$\frac{dx}{dt}=\sigma(y-x)$$
$$\frac{dy}{dt}=-xz+rz-y$$
$$\frac{dz}{dt}=xy-bz$$
变量x,y,z分别是从原始Navier-Stokes方程的温度、密度和速度推导而来，常数r是流体温差的度量，b反映了流体阻尼。
　　Lorenz模型是描述混沌现象第一例有名的方程，由于Lorenz模型将问题简化到只留下三个变量，我们不能借助它来解决实际问题。然而，Lorenz模型展现出来的行为是具有象征性的，任何由这三个方程反映出来的行为都可以在天气问题中找到。因此，想要进一步研究天气问题必须首先解决Lorenz模型中的问题。三个一阶微分方程的求解方法与单摆运动方程类似，值得注意的是我们从书上可以知道运用Euler方法所得到Lorenz模型的数值解有不错的精度。因此我们在这一次的作业中使用Euler方法而非Euler-Cromer方法。

正文

　　这次作业的主要目的是在书本的基础上继续讨论不同情况下各变量之间的关系。

不同的r下x、y、z随时间的变化关系

　　首先，我们讨论在不同的r下x、y、z随时间的变化关系。很明显，r会影响系统的流体运动，取$\sigma=10,b=8/3,r=[5,10,15,25],x(0)=1,y(0)=z(0)=0$。图像如下：


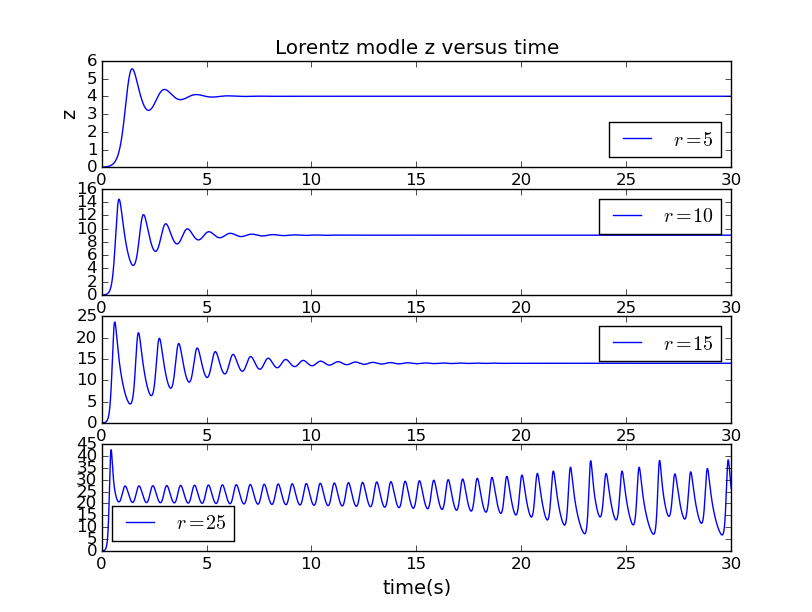
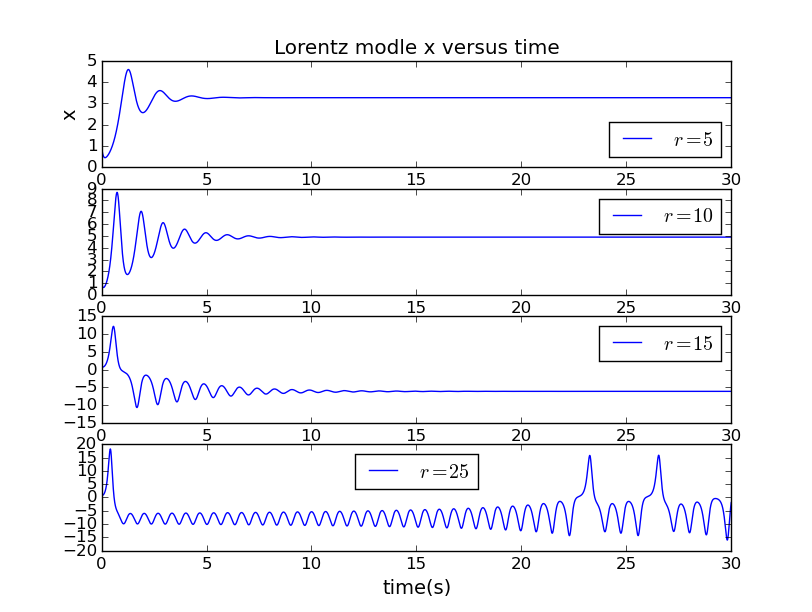
代码在此
由于x、y随时间的变化趋势相同，这里不再给出y随时间的变化图像。

结论

　　当$r$很小的时候，实际作用在流体上的力也很小也就说明流体携带的热量（上下层面的温差）小，这说明$r$其实起着单摆运动方程中外加驱动力$F_D$的作用。可以看出，$r$较小（$r$=5）时不出现混沌现象，系统经过最初的微扰之后恢复稳定，变量值均不再改变；$r$变大后（$r$=10）系统从最初的微扰恢复到稳定状态需要的时间变长；当$r\gt470/19\approx24.74$时，系统出现混沌现象发生强烈的对流，无法恢复至稳定状态，变量变化范围也越来越大。
　　与单摆运动中换个视角用相图来描述其物理性质类似，接下来我们讨论在不同常量取值下三个变量之间的变化关系。

不同的r下z随x的变化关系

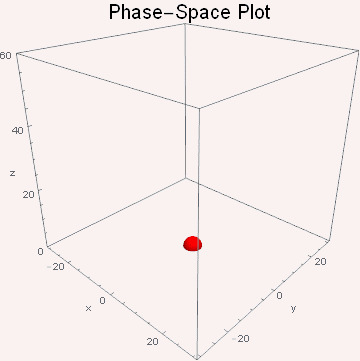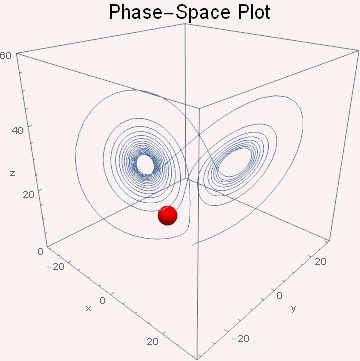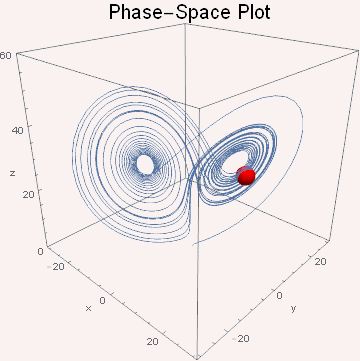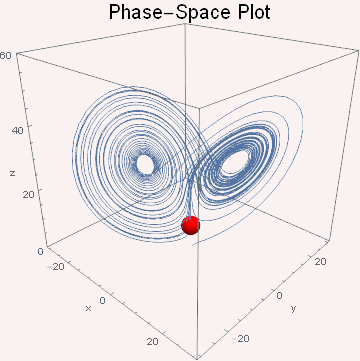
结论

　　可以看出xz相空间轨迹图就是一个类螺旋线。在r较小（r=5）的时候螺旋线较稀疏，轨迹很快就湮灭到中心点；随着r的增大（r=10）螺旋线变密集，绕圈变多，但最终还是湮灭到中心点；随着r的进一步增大（r=15）螺旋线轨迹围着第一个中心点转过第一圈便“转弯”围绕着另一个中心点做螺旋运动并最终湮灭到该中心；当r增大到出现混沌现象时（r=25），轨迹是随机绕着两个中心点交叉做螺旋运动，永不停止。为了方便理解运动轨迹，此处copy了陈洋遥同学的动图。

不同的r下z随x的变化关系(y=0)

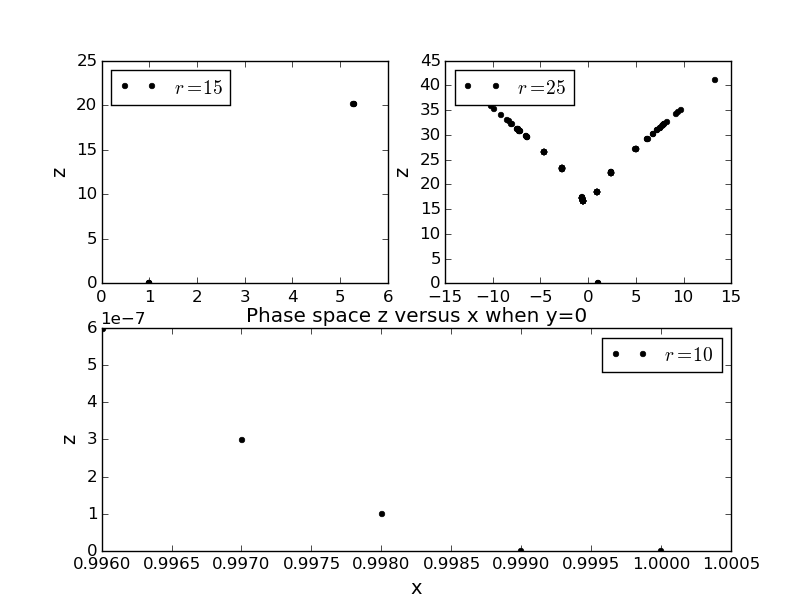
由于z随y变化的图像与z随x变化的图像趋势相同，这里不再给出z随y变化的图像。此外，代码与前类似，这里只给出关键画图的步骤，参考了陈洋遥同学的代码。

    def plot_section_zx(self,_ax,_secy=0.):          
        self.z_sec, self.x_sec = [], []
        self.secy = _secy
        for i in range(len(self.t)):
            if abs(self.y[i]-self.secy)<4E-3:
                self.z_sec.append(self.z[i])
                self.x_sec.append(self.x[i])
        if len(self.z_sec)>0:
            _ax.plot(self.x_sec,self.z_sec,'ok',markersize=4,label=r'$r=10$')
            print 'section plot,secy=',self.secy
            return 1
        else:
            print 'sec_y overranging'
            return 0

结论

　　当y=0时，不同的r下z随x的变化关系其实就是xz相空间的截面图，正好与之前的图一一对应。尽管在r=25时，系统已经出现了混沌现象（见“不同的r下x、y、z随时间的变化关系”），系统变得具有不可重复性、不可确定性，但xz相空间曲线仍然具有规律性（见“不同的r下z随x的变化关系(y=0)”）。因此研究混沌系统的物理规律可以从相空间入手。另外，在这里我们并未规定初值条件，而只规定了y=0，说明相空间的吸引子面与初始条件无关。

结论　

此处不再重复，见上。关于混沌现象，未尽之处我会在期末论文中再进行论述。

致谢

1.教材。
2.陈洋遥同学的一段代码和一张图（具体链接已在正文中给出），非常感谢。
3.百度百科中关于Navier-Stokes方程的介绍。
4.常用数学符号的LaTex表示方法。