对单摆和混沌现象的进一步研究讨论

朱楚楚 2013301510058 材料物理
computationalphysics 期末

摘要：本文主要是对平时作业中未能详尽叙述的物理问题进行进一步分析，首先介绍了两种计算方法：Euler方法和Euler-Cromer方法，接着运用了Euler-Cromer方法详尽讨论了物理量的微小改变对物理单摆运动模型的影响以及Euler方法在Lorentz模型下常数取值对小球运动的影响，展示了相应的相空间运动轨迹图和庞加莱截面图，定性得出了一些结论。本文作为计算物理课程的期末作业，所有程序均已上传到github上“期末作业”的文件夹里。
关键词：物理单摆；混沌现象；Lorentz模型；Euler-Cromer方法；Euler方法；

一、介绍

1.Euler方法和Euler-Cromer方法

　　由于大多数常微分方程初值问题不能求得解析解，所以采用其它近似方法求解是十分重要的。近似方法，如级数解法、逐步逼近法等，可以给出解的近似表达式，通常称为近似解析方法。还有一类近似方法称为数值方法，它可以给出解在一些离散点上的近似值。课本介绍的Euler法（又称切线法）是一种一种最古老、最简单的近似方法，在常微分方程近似数值求解，特别是理论分析中占有很重要的地位。Euler法解微分方程的初值问题是一种利用数值计算获得近似数值解的算法，基本思想是利用差分代替微分，近似得到每一步的数值结果。Euler法的局部截断误差为，分部越密得到的结果越精确。因此要想提高Euler法的精度就要减小Δt的取值。但在某些问题中，不管Δt的取值有多小Euler法精度有多高，计算结果都与实际不符。
　　以最简单的单摆运动为例,能量表达式为

$$E= \frac{1} {2}ml^2 \omega ^2+mgl( 1-cos \theta )$$
小角度运动下可以化为
$$E= \frac{1}{2}ml^2 (\omega ^2+ \frac{g} {l} \theta^2)$$
运用Euler法可以写成
$$E_{i+1}=E_i+\frac {1} {2}mgl( \omega^2_i+\frac{g}{l}\theta^2_i )(\Delta t)^2$$
从式子右边的第二项就可以看出来，不管Δt取多小，系统的能量值都不是守恒的。Euler法的精度再高，对此类问题也不适用。因此人们又在此基础上提出了改进Euler法、四阶Runge-Kutta方法、单步法、线性多步法、Euler-Cromer法。其中Euler-Cromer法通过对Euler法做了一点小改动（以简单单摆为例，Euler法：$\theta_{ i+1 }=\theta_{ i}+\omega_i\Delta t$，Euler-Cromer法：$\theta_{ i+1 }=\theta_{ i}+\omega_{i+1}\Delta t$），将算法的精度和稳定性都提高不少。

2.混沌现象

　　单摆是物理学中最简单的物理模型之一，但当其振幅没有限制时，具有意想不到的复杂性——混沌。混沌是指发生在确定性系统中的貌似随机的不规则运动。一个确定性理论描述的系统，其行为却表现为不确定性、不可重复、不可预测，这就是混沌现象。进一步的研究表明，混沌是非线性动力学系统的固有特性。目前人们把混沌看成是一种无周期的有序。它包括如下特征：
（1）内在随机性。混沌系统是由完全确定的方程描述的，无需附加任何随机因数，但系统仍会表现出类似随机性的行为；
（2）分形性质。混沌吸引子（Lorenz吸引子、Henon吸引子）由分数维数刻画；
（3）标度不变性。在由分岔导致混沌的过程中，混沌遵从Feigenbaum常数系；
（4）对初值条件的敏感依赖性。只要初始条件稍有偏差或微小的扰动，则会使得系统的长期行为、最终状态出现巨大的差异。因此混沌系统的长期演化行为是不可预测的；
（5）混沌内部具有自相似性。

3.Lorentz模型

　　为了从更基础的角度来理解天气问题中的混沌现象，大气科学家E.N.Lorentz从描述粘性不可压缩流体动量守恒的运动方程——Navier-Stokes方程出发，在rayleigh-benard问题下对其进行简化得到Lorenz模型用于描述大气对流。
　　Lorenz模型是描述混沌现象第一例有名的方程，Lorentz方程揭示了与经典力学不同的高度初值敏感性、运动的不可预测性和解的非稳定性，Lorentz将其形象地解释为“蝴蝶效应”。由于Lorenz模型将问题简化到只留下三个变量，我们不能借助它来解决实际问题。然而，Lorenz模型展现出来的行为是具有象征性的，任何由这三个方程反映出来的行为都可以在天气问题中找到。因此，想要进一步研究天气问题必须首先解决Lorenz模型中的问题。三个一阶微分方程的求解方法与单摆运动方程类似，值得注意的是我们从书上可以知道运用Euler方法所得到Lorenz模型的数值解有不错的精度，因此使用Euler方法解决。

二、正文

1 物理单摆运动模型

将所有实际情况中可能出现的因素都考虑进单摆的运动：大角度（任意角度）、空气阻力、增加驱动力，就得到了复杂性远高于简单单摆模型的非线性阻尼动力摆，称为“物理单摆”。首先给出非线性阻尼动力摆的微分运动方程：

$$\frac{ d\theta }{ dt }=\omega$$
$$\frac{ d\omega }{ dt }=-\frac{ g }{ l }\theta-q\omega+F_D sin( \Omega_D t )$$
式子中$g$是重力加速度，$l$是绳长，$\Omega_D$是驱动力角速度，$F_D$是驱动力系数，q是耗散力系数。运用Euler-Cromer法给出微分方程的数值解（此处不再给出表达式）。图1是对非线性阻尼动力摆取不同的初值条件运用Euler-Cromer法编写程序得到的单摆运动随时间演化的结果。取值：$q=1/2,\theta(0)=0,\omega( 0 )=0,\Omega_D=2/3,dt=0.04,l=g=9.8,F_D=[0.5,1.2,1.201 ]$

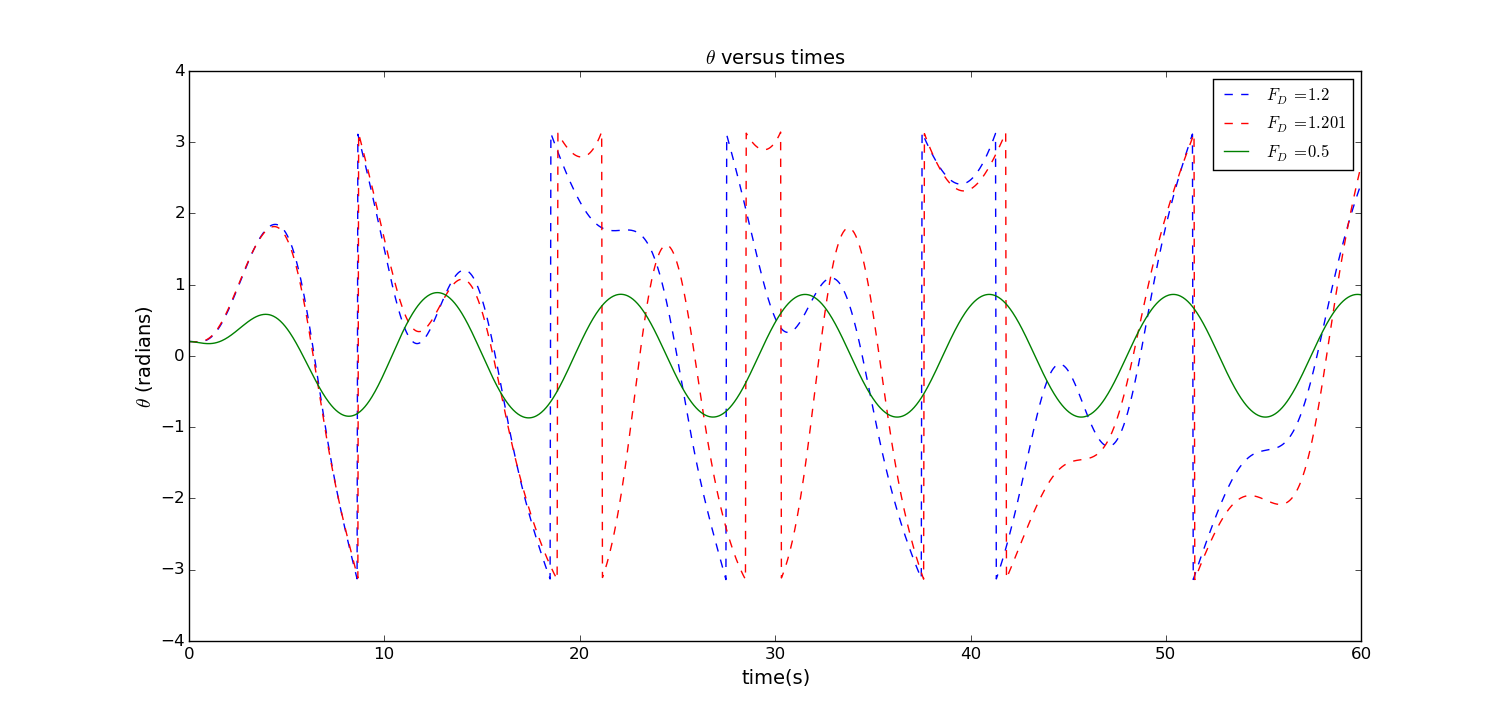
图1.如图，关于非线性阻尼动力摆，θ作为时间t的函数。从图中可以看出$F_D$=0.5时经过开始的暂态过渡后单摆做稳定的简谐运动，$F_D$=1.2时单摆运动轨迹无规律，出现混沌现象。此时对做微小改动（红色虚线曲线），单摆轨迹在前20s几乎重叠，超过20s后单摆轨迹相差越来越大，不符合经典力学中解的稳定性（当初始条件出现微小改变时解也出现微小改变），因此无法根据已有的实验结果预测其他实验条件下的结果。天气作为一个典型的混沌系统，无法进行长期预判。

从上面的分析我们已经可以确定混沌系统下θ随时间t的变化不可预测，看起来混沌系统似乎无从下手进行分析预测，但是实验表明即使是混沌系统，在θω空间也有可能做出关于θ的精确预测。因此我们选择在θω空间研究混沌现象，θω空间被称为相空间。相空间中对θ的描述如图2所示。通过图2我们可以观察到吸引子的存在。一个系统有朝某个稳态发展的趋势，这个稳态就叫做吸引子。吸引子分为平庸吸引子和奇异吸引子。奇异吸引子是混沌系统的另一个重要的特征。简单地说奇异吸引子就是相空间一个有限的区域内，由无穷多个不稳定点集组成的一个集合体，它对初值条件有高度敏感性。

图2.如图，关于非线性阻尼动力摆，相空间中θ作为ω的函数。，其余取值同图1,相比看不出任何规律的θ(t)图，相空间的θ(ω)图忽略了变化时间的信息而描述了动力学系统的全局显得更有规律。图中可以观察到平庸吸引子（图2左上角曲线）和奇异吸引子。
代码在此

在作业中我们定性地发现q和对单摆运动的影响恰好相反，因此此处不再赘述。
　　如果我们在相图中观察θ(ω)图时还规定，又可以得到不一样的结果。如图3所示。这种相空间图称为庞加莱截面，其基本思想是在多维相空间(x,dx,ldt,xz,d²x /dt²,…,dR /dt)中适当选取一截面，在此截面上某一对共扼变量如xdx, ldt取固定值，称此截面为庞加莱截面。观测庞加莱截面，相空间的连续轨迹表现为一些离散点之间的映射。由它们可得到关于运动特性的信息。不考虑初始阶段的暂态过渡过程，只考虑庞加莱截面的稳态图像，当图像只有一个不动点和少数离散点时，可判定运动是周期的；当图像是一封闭曲线时，可判定运动是准周期的；当图像是成片的密集点，且有层次结构时，可判定运动处于混沌状态。

图3.如图，关于非线性阻尼动力摆，θ作为ω的函数且θ与ω同相。取值如图，其余未说明的量取值同图1。
代码在此

2 Lorentz模型

　　　Lorentz方程式如下：

$$\frac{dx}{dt}=\sigma(y-x)$$
$$\frac{dy}{dt}=-xz+rx-y$$
$$\frac{dz}{dt}=xy-bz$$
变量x,y,z分别是从原始方程的温度，密度和速度推导而来；σ、r、b是常数，r、b分别反映了流体温差和阻尼。
　　　对于Lorentz模型的分析和非线性阻尼动力摆一样，θ类比z(x、y)，ω类比x(y、z)，σ、r、b类比q、$F_D$。画出相图和庞加莱截面分析，此处不重复叙述过程，仅给出结果如图4,图5。取值：$\sigma=10,b=8/3,r=[5,10,15,25],x(0)=1,y(0)=z(0)=0$

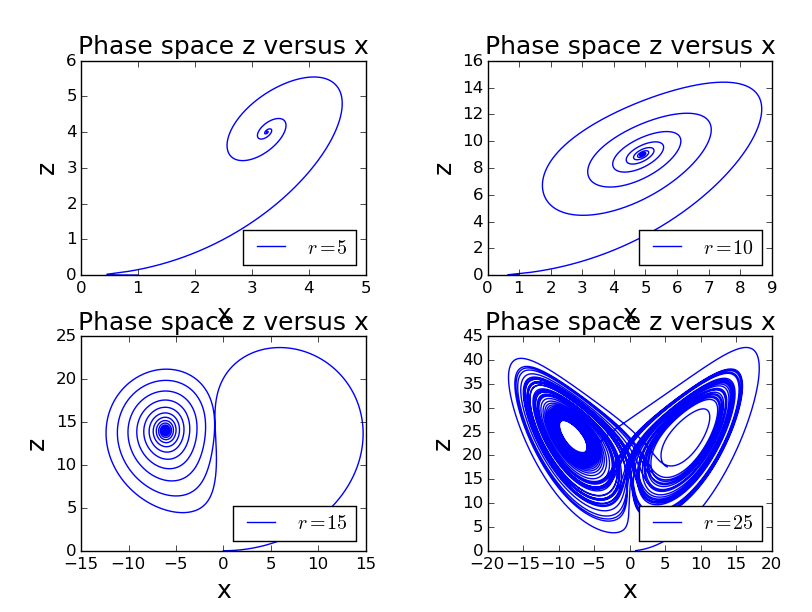
图4.如图显示了不同r取值下Lorentz模型xz相空间轨迹。
代码在此

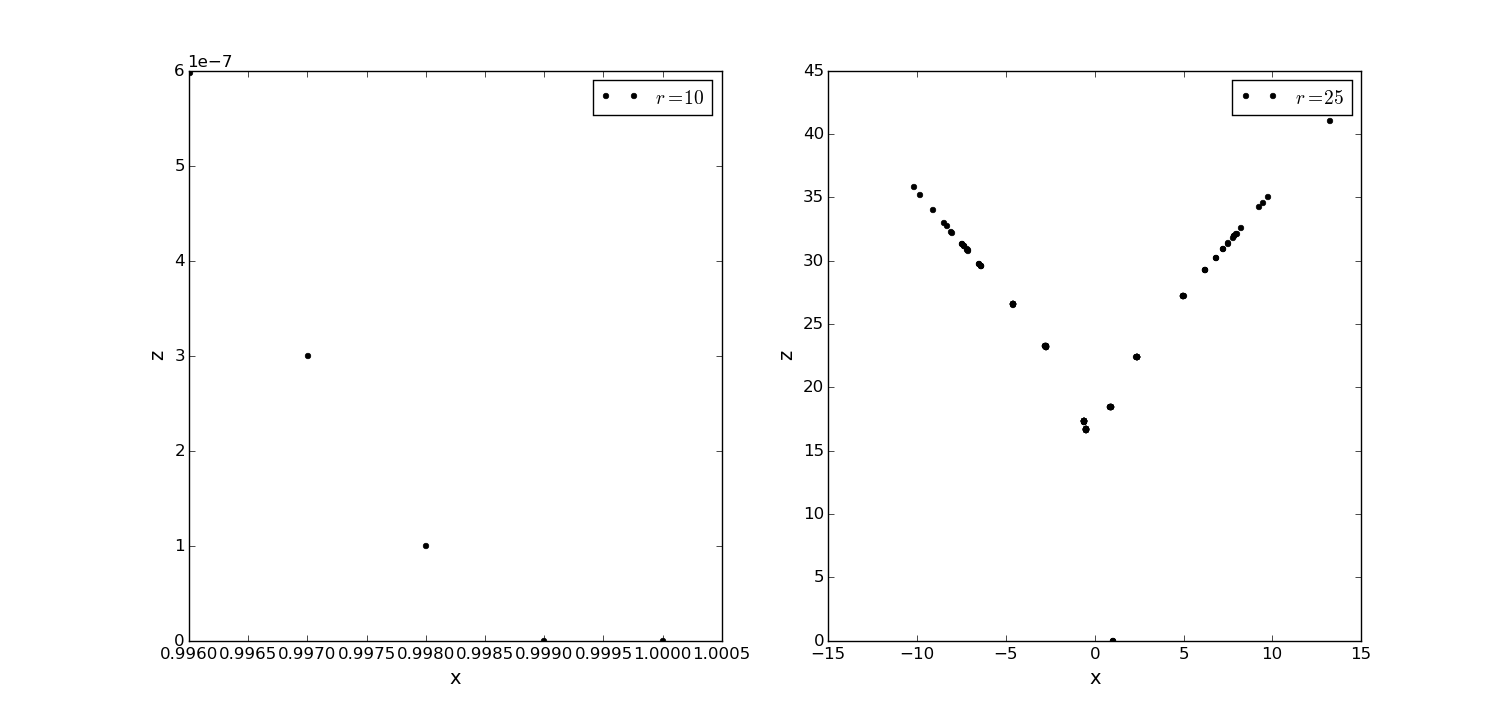
图5.如图显示了两个r取值下Lorentz模型xz相空间庞加莱截面。t=60s，其余取值同前。r=25的图形只在t=30s之后才会出现。
代码在此

三、结语

1.通过我们的模拟可以发现，图像确实符合混沌现象所描述的几个特点，一是初值的细微改变会导致结果相去甚远，二是系统虽由运动方程确定给出，但行为却是不可预测的十分混乱的；
2.根据判断可知在不同初值条件下的物理单摆运动中q=0=0对应准周期运动，q=0.5=0.5对应周期运动，q=0.5=1.2对应混沌状态。
3.可以看出Lorentz模型下xz相空间轨迹图就是一个类螺旋线。在r较小（r=5）的时候螺旋线较稀疏，轨迹很快就湮灭到中心点；随着r的增大（r=10）螺旋线变密集，绕圈变多，但最终还是湮灭到中心点；随着r的进一步增大（r=15）螺旋线轨迹围着第一个中心点转过第一圈便“转弯”围绕着另一个中心点做螺旋运动并最终湮灭到该中心；当r增大到出现混沌现象时（r=25），轨迹是随机绕着两个中心点交叉做螺旋运动，永不停止。

四、致谢

[1]Computational Physics, Nicholas J. Giordano & Hisao Nakanishi
[2]欧拉法与Matlab数值求解，陈誌敏