第十一次作业

chapter4 exercise4.7、4.9、4.11

朱楚楚 材料物理 2013301510058
computationalphysics chapter4

---

摘要

双星运动；万有引力定律；

背景

　　万有引力定律的发现，是17世纪自然科学最伟大的成果之一。它把地面上物体运动的规律和天体运动的规律统一了起来，并第一次解释了自然界中四种基本相互作用之一的规律，在人类认识自然的历史上树立了一座里程碑。万有引力定律揭示了天体运动的规律，为实际的天文观测提供了一套计算方法，可以只凭少数观测资料，就能算出长周期运行的天体运动轨道。利用万有引力公式，开普勒第三定律等还可以计算太阳、地球等无法直接测量的天体的质量。
　　万有引力定律告诉我们任意两个质点有通过连心线方向上的力相互吸引。该引力大小与它们质量的乘积成正比与它们距离的平方成反比，与两物体的化学组成和其间介质种类无关。运用到地球和太阳两者间的吸引力为

$$F_G=\frac{GM_SM_E}{r^2}$$
其中$M_S、M_E$是太阳和地球的质量，$r$是太阳和地球间的距离，$G$是万有引力常数。由于天体的质量巨大，两天体相隔距离也大到与日常生活认知中的距离无法比拟，因此使用国际单位制来描述天体运动十分麻烦，因此引入天文单位$1Au$=地球到太阳的平均距离$\approx1.5\times10^{11}m$，时间也用年（$1\ year\approx3.2\times10^{7}s$）来描述。
　　在第三章中我们阐述了Euler方法不能很好地适用于简谐问题。在描述天体运动的时候使用Euler方法会得出行星运动过程中能量不断增大、轨迹逐渐远离太阳等违背事实的结果，同样要使用Euler-Cromer方法给出数值解。
　　本文主要讨论在太阳与行星质量相近或相等，太阳的运动不能被忽略时的双星系统以及当引力不是距离的平方反比时行星的运动轨迹。

正文

双星系统（$M_1=aM_2$）

　　由于此时行星和太阳质量相近，行星和太阳的地位相等，因此方程对太阳和行星均适用，不再赘述，仅加脚标区分，太阳记为1,行星记为2。

$$F_1=F_2=F=\frac{GM_1M_2}{r^2}$$
　　我们首先写出太阳、行星运动微分方程，化简方法同前：
$$\begin{cases}\frac{d^2x_1}{dt^2}=\frac{F_x}{M_1}=-\frac{GM_1M_2}{r^2}cos\theta=-\frac{GM_1M_2x_1}{r^3}\\ \frac{d^2y_1}{dt^2}=\frac{F_y}{M_1}=-\frac{GM_1M_2}{r^2}sin\theta=-\frac{GM_1M_2y_1}{r^3}\end{cases}$$
　　　　　太阳：$\begin{cases} \frac{dv_{x1}}{dt}=-\frac{GM_2x_1}{r^3}\\ \frac{dx_1}{dt}=v_{x1}\\ \frac{dv_{y1}}{dt}=-\frac{GM_2y_2}{r^3}\\ \frac{dy_1}{dt}=v_{y1}\\\end{cases}$&行星：$\begin{cases} \frac{dv_{x2}}{dt}=-\frac{GM_1x_2}{r^3}\\ \frac{dx_2}{dt}=v_{x2}\\ \frac{dv_{y2}}{dt}=-\frac{GM_1y_2}{r^3}\\ \frac{dy_2}{dt}=v_{y2}\\\end{cases}$
行星轨迹近似为圆形，有
行星：$\frac{M_2v_2^2}{r}=F=\frac{GM_1M_2}{r^2} \Rightarrow GM_1=v_2^2r=4\pi^2/r^2(AU^3/year)$
太阳：$\frac{M_1v_1^2}{r}=F=\frac{GM_1M_2}{r^2} \Rightarrow GM_2=v_1^2r=\frac{4\pi^2/r^2}{a}(AU^3/year)$
Euler-Cromer方法给出数值解：
太阳： $$\begin{cases} v_{x1,i+1}=v_{x1,i}-\frac{1}{a}\cdot\frac{4\pi^2x_{1i}}{r_i^3}\Delta t\\ x_{1,i+1}=x_{1,i}+v_{x1,i+1}\Delta t\\ v_{y1,i+1}=v_{y1,i}-\frac{1}{a}\cdot\frac{4\pi^2y_{1i}}{r_i^3}\Delta t\\ y_{1,i+1}=y_{1,i}+v_{y1,i+1}\Delta t\\ \end{cases}$$
&行星： $$\begin{cases} v_{x2,i+1}=v_{x2,i}-\frac{4\pi^2x_{2i}}{r_i^3}\Delta t\\ x_{2,i+1}=x_{2,i}+v_{x2,i+1}\Delta t\\ v_{y2,i+1}=v_{y2,i}-\frac{4\pi^2y_{2i}}{r_i^3}\Delta t\\ y_{2,i+1}=y_{2,i}+v_{y2,i+1}\Delta t\\ \end{cases}$$
取值：$v_{x1}=0,v_{y1}=\frac{1}{3}\sqrt{6\pi},x_1(0)=0,y_1(0)=0.5,v_{x2}=0,v_{y2}=-\frac{2}{3}\sqrt{6\pi},x_2(0)=0,y_2(0)=-0.5$
图像如下：

代码在此

引力不是距离的平方反比

　　设引力表达式为$F_G=\frac{GM_SM_E}{r^\beta}$，当$\beta=2$时，即为万有引力定律所满足的情况，接下来考虑$\beta\neq2$的情况。注意，此时要将太阳的运动固定。图像如下：


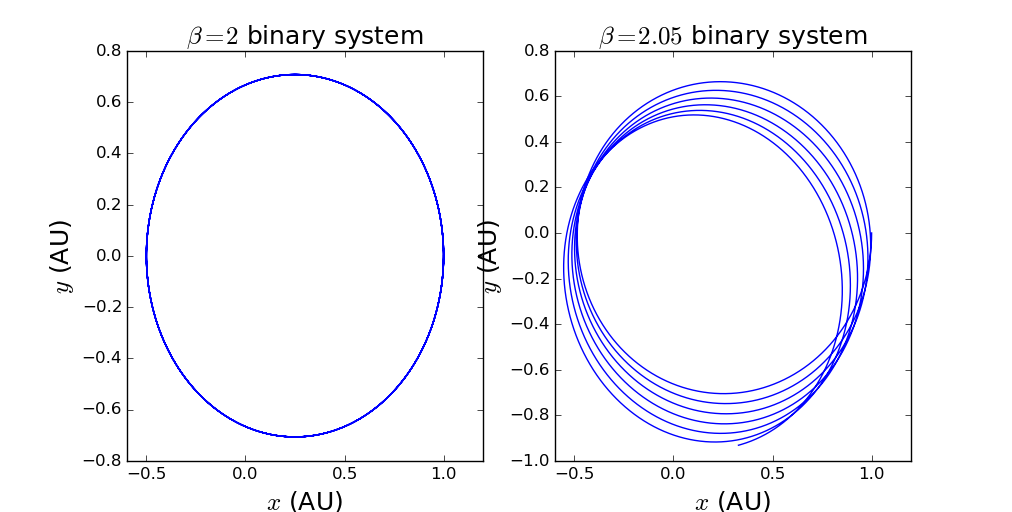
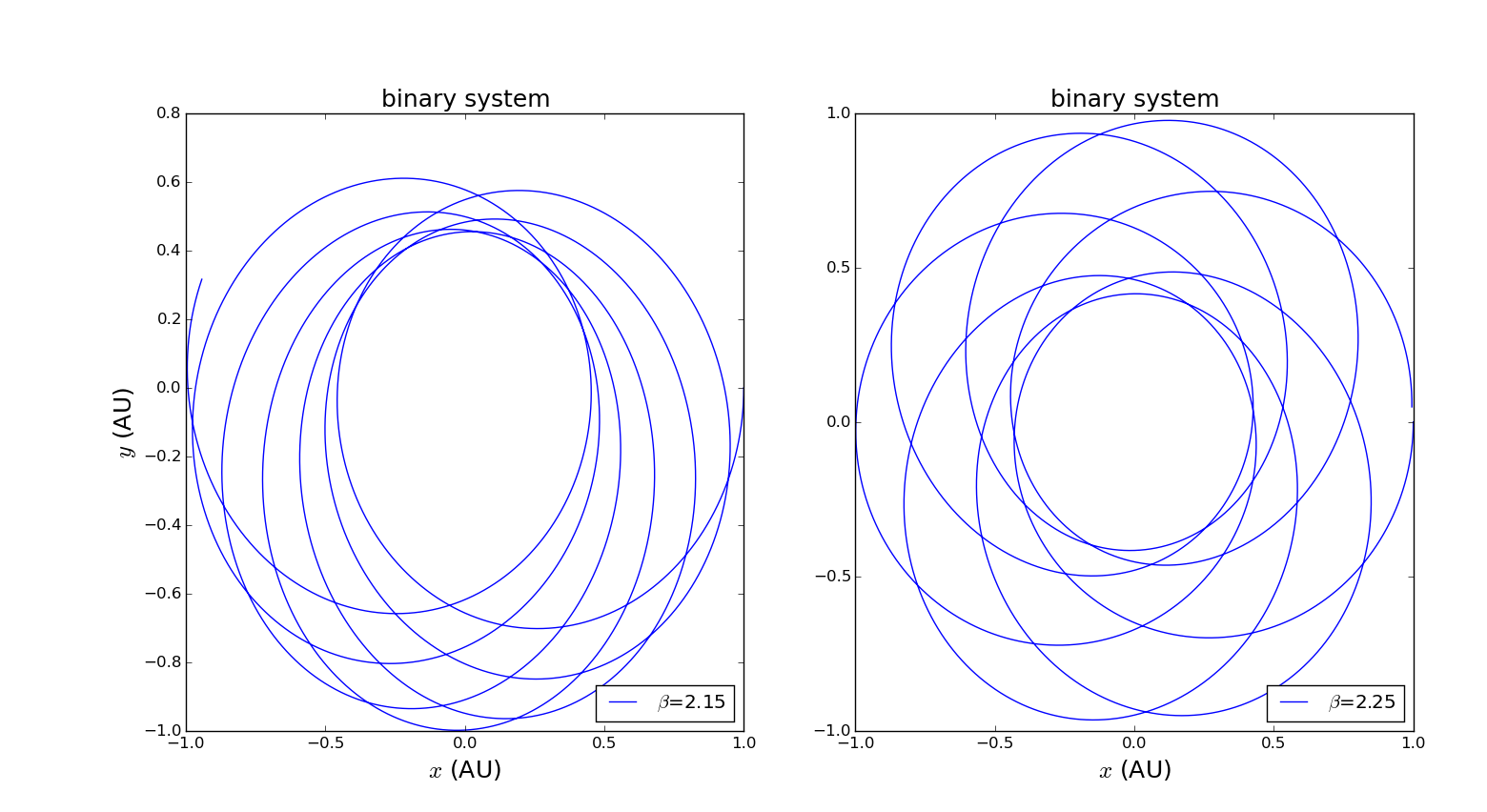
代码在此

结论

1.在适当的初始条件下双星系统可以呈现“同心圆”运动。而当太阳质量是行星质量的三倍时，双星系统出现螺旋运动，太阳螺旋上升行星螺旋下降，运动半径均不变;
2.当引力不是距离的平方反比（$\beta\neq2$）时，双星系统运动不再是闭合的椭圆（圆）轨迹而是不断进动；
3.由于论述中均采用同一初值条件，因此无法探讨初值给双星系统带来的影响。

致谢

1.百度百科万有引力
2.教材
3.照例感谢陈洋遥同学的此段代码以及他所做出酷炫的动图给我的一点小提示，十分感谢