[关闭]
@Yano 2015-12-30T11:21:54.000000Z 字数 17359 阅读 12982

LeetCode之Hash Table题目汇总

LeetCode

我的博客：http://blog.csdn.net/yano_nankai
LeetCode题解：https://github.com/LjyYano/LeetCode

LeetCode 题目汇总

LeetCode之Array题目汇总
LeetCode之Hash Table题目汇总
LeetCode之Linked List题目汇总
LeetCode之Math题目汇总
LeetCode之String题目汇总
LeetCode之Binary Search题目汇总
LeetCode之Divide and Conquer题目汇总
LeetCode之Dynamic Programming题目汇总
LeetCode之Backtracing题目汇总
LeetCode之Stack题目汇总
LeetCode之Sort题目汇总
LeetCode之Bit Manipulation题目汇总
LeetCode之Tree题目汇总
LeetCode之Depth-first Search题目汇总
LeetCode之Breadth-first Search题目汇总
LeetCode之Graph题目汇总
LeetCode之Trie题目汇总
LeetCode之Design题目汇总

文章目录：

Group Anagrams

Given an array of strings, group anagrams together.

For example, given: ["eat", "tea", "tan", "ate", "nat", "bat"], 
Return:

[
  ["ate", "eat","tea"],
  ["nat","tan"],
  ["bat"]
]

Note:

  1. For the return value, each inner list's elements must follow the lexicographic order.
  2. All inputs will be in lower-case.
  1. 把每个string，按照字母分组，如”abc”和”cba”是一组
  2. 维护一个map，key是abc，value是abc一组string出现的下标
  3. 把每一组string找出，排序，加入结果
  1.     public List<List<String>> groupAnagrams(String[] strs) {
  3.         if (strs == null || strs.length == 0) {
  4.             return new ArrayList<List<String>>();
  5.         }
  7.         List<List<String>> rt = new ArrayList<List<String>>();
  9.         Map<String, ArrayList<Integer>> map = new HashMap<String, ArrayList<Integer>>();
  11.         // 把单词分组
  12.         for (int i = 0; i < strs.length; i++) {
  13.             char[] c = strs[i].toCharArray();
  14.             Arrays.sort(c);
  15.             String k = Arrays.toString(c);
  16.             ArrayList<Integer> list = new ArrayList<Integer>();
  17.             if (map.containsKey(k)) {
  18.                 list = map.get(k);
  19.             }
  20.             list.add(i);
  21.             map.put(k, list);
  22.         }
  24.         for (String s : map.keySet()) {
  26.             List<Integer> l = map.get(s);
  27.             List<String> group = new ArrayList<String>();
  29.             // 把相同字母的单词放入同一个list
  30.             for (Integer i : l) {
  31.                 group.add(strs[i]);
  32.             }
  34.             // 按字典序排序
  35.             group.sort(new Comparator<String>() {
  36.                 public int compare(String x, String y) {
  37.                     return x.compareTo(y);
  38.                 }
  39.             });
  41.             rt.add(group);
  42.         }
  44.         return rt;
  45.     }

Bulls and Cows

You are playing the following Bulls and Cows game with your friend: You write down a number and ask your friend to guess what the number is. Each time your friend makes a guess, you provide a hint that indicates how many digits in said guess match your secret number exactly in both digit and position (called "bulls") and how many digits match the secret number but locate in the wrong position (called "cows"). Your friend will use successive guesses and hints to eventually derive the secret number.

For example:

Secret number: "1807"
Friend's guess: "7810"

Hint: 1 bull and 3 cows. (The bull is 8, the cows are 0, 1 and 7.)

Write a function to return a hint according to the secret number and friend's guess, use A to indicate the bulls and B to indicate the cows. In the above example, your function should return "1A3B".

Please note that both secret number and friend's guess may contain duplicate digits, for example:

  1. Secret number:  "1123"
  2. Friend's guess: "0111"

In this case, the 1st 1 in friend's guess is a bull, the 2nd or 3rd 1 is a cow, and your function should return "1A1B".

You may assume that the secret number and your friend's guess only contain digits, and their lengths are always equal.

Credits:
Special thanks to @jeantimex for adding this problem and creating all test cases.

  1.     public String getHint(String secret, String guess) {
  3.         if (secret == null || guess == null
  4.                 || secret.length() != guess.length()) {
  5.             return "";
  6.         }
  8.         char[] s = secret.toCharArray();
  9.         char[] g = guess.toCharArray();
  11.         int A = 0, B = 0, n = s.length;
  13.         // 统计bulls
  14.         for (int i = 0; i < n; i++) {
  15.             if (s[i] == g[i]) {
  16.                 s[i] = '#';
  17.                 g[i] = '#';
  18.                 A++;
  19.             }
  20.         }
  22.         // 统计cows
  24.         Map<Character, Integer> map = new HashMap<Character, Integer>();
  26.         for (int i = 0; i < n; i++) {
  27.             if (s[i] != '#') {
  28.                 if (!map.containsKey(s[i])) {
  29.                     map.put(s[i], 1);
  30.                 } else {
  31.                     int times = map.get(s[i]);
  32.                     times++;
  33.                     map.put(s[i], times);
  34.                 }
  35.             }
  36.         }
  38.         for (int i = 0; i < n; i++) {
  39.             if (g[i] != '#') {
  40.                 if (map.containsKey(g[i]) && map.get(g[i]) != 0) {
  41.                     int times = map.get(g[i]);
  42.                     times--;
  43.                     map.put(g[i], times);
  44.                     B++;
  45.                 }
  46.             }
  47.         }
  49.         return A + "A" + B + "B";
  50.     }

Count Primes

Description:

Count the number of prime numbers less than a non-negative number, n.

Credits:
Special thanks to @mithmatt for adding this problem and creating all test cases.

Hint:

  1. Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of _isPrime_function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better?

  2. As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better?

  3. Let's write down all of 12's factors:

    2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12

    As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.

    Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?

    public int countPrimes(int n) {
   int count = 0;
   for (int i = 1; i < n; i++) {
      if (isPrime(i)) count++;
   }
   return count;
}

private boolean isPrime(int num) {
   if (num <= 1) return false;
   // Loop's ending condition is i * i <= num instead of i <= sqrt(num)
   // to avoid repeatedly calling an expensive function sqrt().
   for (int i = 2; i * i <= num; i++) {
      if (num % i == 0) return false;
   }
   return true;
}

  4. The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.


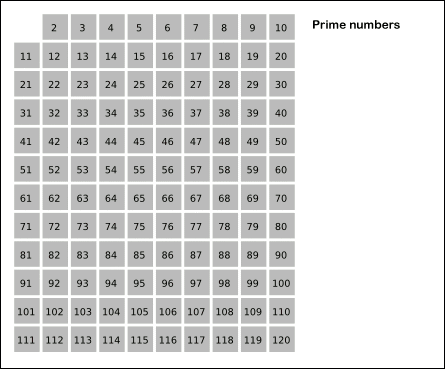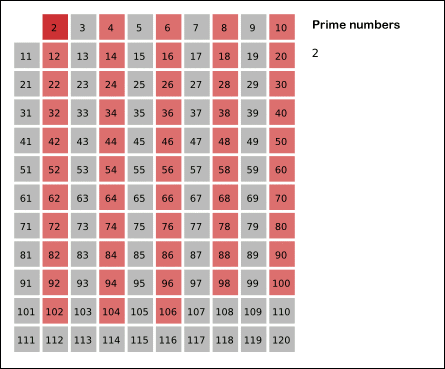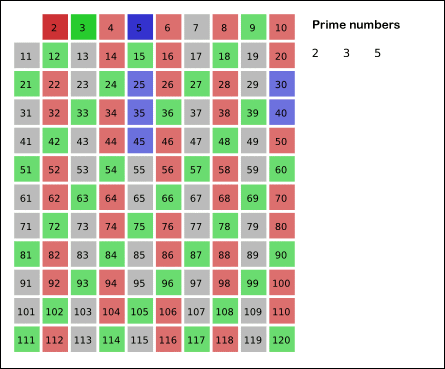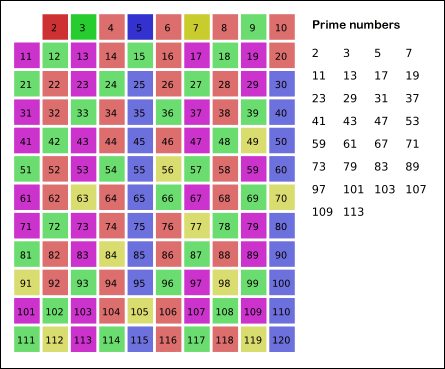
    Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.

    We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well?

  5. 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off?

  6. In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2_p_, ... Now what should be the terminating loop condition?

  7. It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3?

  8. Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.

    The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.

      public int countPrimes(int n) {
       boolean[] isPrime = new boolean[n];
       for (int i = 2; i < n; i++) {
          isPrime[i] = true;
       }
       // Loop's ending condition is i * i < n instead of i < sqrt(n)
       // to avoid repeatedly calling an expensive function sqrt().
       for (int i = 2; i * i < n; i++) {
          if (!isPrime[i]) continue;
          for (int j = i * i; j < n; j += i) {
             isPrime[j] = false;
          }
       }
       int count = 0;
       for (int i = 2; i < n; i++) {
          if (isPrime[i]) count++;
       }
       return count;
    }

  1.     public int countPrimes(int n) {
  3.         boolean[] b = new boolean[n];
  5.         // 将非质数标记为true
  6.         for (int i = 2; i * i < n; i++) {
  7.             if (b[i] == false) {
  8.                 for (int j = i; i * j < n; j++) {
  9.                     b[i * j] = true;
  10.                 }
  11.             }
  12.         }
  14.         // count
  15.         int c = 0;
  16.         for (int i = 2; i < n; i++) {
  17.             if (b[i] == false) {
  18.                 c++;
  19.             }
  20.         }
  22.         return c;
  23.     }

Fraction to Recurring Decimal

Given two integers representing the numerator and denominator of a fraction, return the fraction in string format.

If the fractional part is repeating, enclose the repeating part in parentheses.

For example,

Credits:
Special thanks to @Shangrila for adding this problem and creating all test cases.

  1.     public String fractionToDecimal(int numerator, int denominator) {
  3.         String sign = "";
  5.         if (Math.signum(numerator) * Math.signum(denominator) < 0) {
  6.             sign = "-";
  7.         }
  9.         long n = Math.abs(numerator);
  10.         long d = Math.abs(denominator);
  12.         String intPart = Math.abs(n / d) + "";
  14.         // 如果整除，直接返回结果
  15.         if (n % d == 0) {
  16.             return sign + intPart;
  17.         }
  19.         // 计算小数部分
  20.         n %= d;
  21.         n *= 10;
  23.         StringBuilder sb = new StringBuilder();
  24.         Map<Long, Integer> mod = new HashMap<Long, Integer>();
  26.         for (int i = 0; n != 0; i++) {
  28.             long q = n / d;
  30.             Integer start = mod.get(n / 10);
  32.             if (start != null) {
  33.                 sb.insert(start, "(");
  34.                 sb.append(")");
  35.                 break;
  36.             }
  38.             sb.append(Math.abs(q));
  39.             mod.put(n / 10, i);
  41.             n %= d;
  42.             n *= 10;
  43.         }
  45.         String fractionalPart = sb.toString();
  47.         return sign + intPart + "." + fractionalPart;
  48.     }

H-Index

Given an array of citations (each citation is a non-negative integer) of a researcher, write a function to compute the researcher's h-index.

According to the definition of h-index on Wikipedia: "A scientist has index h if h of his/her N papers have at least h citations each, and the other N − h papers have no more than h citations each."

For example, given citations = [3, 0, 6, 1, 5], which means the researcher has 5 papers in total and each of them had received 3, 0, 6, 1, 5 citations respectively. Since the researcher has 3 papers with at least 3 citations each and the remaining two with no more than 3 citations each, his h-index is 3.

Note: If there are several possible values for h, the maximum one is taken as the h-index.

Hint:

  1. An easy approach is to sort the array first.
  2. What are the possible values of h-index?
  3. A faster approach is to use extra space.

Credits:
Special thanks to @jianchao.li.fighter for adding this problem and creating all test cases.

题目描述不清，实际上，H-Index的核心计算方法是：

1、将某作者的所有文章的引用频次按照从大到小的位置排列

2、从前到后，找到最后一个满足条件的位置，其条件为：此位置是数组的第x个，其值为y，必须满足 y >= x;

  1.     public int hIndex(int[] citations) {
  3.         if (citations == null) {
  4.             return 0;
  5.         }
  7.         int h = 0, n = citations.length;
  8.         Arrays.sort(citations);
  10.         for (int i = n - 1; i >= 0; i--) {
  11.             if (citations[i] >= n - i) {
  12.                 h = n - i;
  13.             } else {
  14.                 break;
  15.             }
  16.         }
  18.         return h;
  19.     }

H-Index II

Follow up for H-Index: What if the citations array is sorted in ascending order? Could you optimize your algorithm?

Hint:

  1. Expected runtime complexity is in O(log n) and the input is sorted.

二分查找

  1.     public int hIndex(int[] citations) {
  3.         int n = citations.length;
  4.         int low = 0, high = n - 1;
  6.         while (low <= high) {
  8.             int mid = low + (high - low) / 2;
  10.             if (citations[mid] == n - mid) {
  11.                 return n - mid;
  12.             } else if (citations[mid] < n - mid) {
  13.                 low = mid + 1;
  14.             } else {
  15.                 high = mid - 1;
  16.             }
  18.         }
  20.         return n - low;
  21.     }

Happy Number

Write an algorithm to determine if a number is "happy".

A happy number is a number defined by the following process: Starting with any positive integer, replace the number by the sum of the squares of its digits, and repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1. Those numbers for which this process ends in 1 are happy numbers.

**Example: **19 is a happy number

Credits:
Special thanks to @mithmatt and @ts for adding this problem and creating all test cases.

1. 使用set

对每一个计算的结果进行计算，如果是1则是Happy Number；不是1且在set中出现过，则不是返回false；否则将结果加入set。

2. 利用性质，特殊数字“4”

在某一时刻，出现了4的Number肯定不Happy。

1000以内的Happy Number是：

  1. 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167, 176, 188, 190, 192, 193, 203, 208, 219, 226, 230, 236, 239, 262, 263, 280, 291, 293, 301, 302, 310, 313, 319, 320, 326, 329, 331, 338, 356, 362, 365, 367, 368, 376, 379, 383, 386, 391, 392, 397, 404, 409, 440, 446, 464, 469, 478, 487, 490, 496, 536, 556, 563, 565, 566, 608, 617, 622, 623, 632, 635, 637, 638, 644, 649, 653, 655, 656, 665, 671, 673, 680, 683, 694, 700, 709, 716, 736, 739, 748, 761, 763, 784, 790, 793, 802, 806, 818, 820, 833, 836, 847, 860, 863, 874, 881, 888, 899, 901, 904, 907, 910, 912, 913, 921, 923, 931, 932, 937, 940, 946, 964, 970, 973, 989, 998, 1000

13和31，101和11是一样的，只是对每个数字的排列组合，那么不同序列的数字是：

  1. 1, 7, 13, 19, 23, 28, 44, 49, 68, 79, 129, 133, 139, 167, 188, 226, 236, 239, 338, 356, 367, 368, 379, 446, 469, 478, 556, 566, 888, 899

500以内的Happy Primes（质数）

  1. 7, 13, 19, 23, 31, 79, 97, 103, 109, 139, 167, 193, 239, 263, 293, 313, 331, 367, 379, 383, 397, 409, 487
  1.     public boolean isHappy(int n) {
  3.         if (n < 1) {
  4.             return false;
  5.         }
  7.         if (n == 1) {
  8.             return true;
  9.         }
  11.         Set<Integer> set = new HashSet<Integer>();
  12.         set.add(n);
  14.         while (true) {
  15.             int s = 0;
  16.             while (n > 0) {
  17.                 s += (n % 10) * (n % 10);
  18.                 n /= 10;
  19.             }
  20.             System.out.println(s);
  21.             if (s == 1) {
  22.                 return true;
  23.             } else if (set.contains(s)) {
  24.                 return false;
  25.             }
  26.             set.add(s);
  27.             n = s;
  28.         }
  29.     }
  1.     public boolean isHappy2(int n) {
  3.         if (n < 1) {
  4.             return false;
  5.         }
  7.         if (n == 1) {
  8.             return true;
  9.         } else if (n == 4) {
  10.             return false;
  11.         }
  13.         int s = 0;
  14.         while (n > 0) {
  15.             s += (n % 10) * (n % 10);
  16.             n /= 10;
  17.         }
  19.         return isHappy2(s);
  20.     }

Isomorphic Strings

Given two strings s and t, determine if they are isomorphic.

Two strings are isomorphic if the characters in s can be replaced to get t.

All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character but a character may map to itself.

For example,
Given "egg", "add", return true.

Given "foo", "bar", return false.

Given "paper", "title", return true.

Note:
You may assume both s and t have the same length.

保证一对一的映射关系，即字母e映射了a，则不能再表示自身

  1.     public boolean isIsomorphic(String s, String t) {
  3.         if (s == null || t == null) {
  4.             return false;
  5.         }
  7.         if (s.length() != t.length()) {
  8.             return false;
  9.         }
  11.         Map<Character, Character> map = new HashMap<Character, Character>();
  12.         Set<Character> set = new HashSet<Character>();
  14.         for (int i = 0; i < s.length(); i++) {
  15.             char c1 = s.charAt(i);
  16.             char c2 = t.charAt(i);
  18.             // 保证一对一的映射关系
  19.             if (map.containsKey(c1)) {
  20.                 if (map.get(c1) != c2) {
  21.                     return false;
  22.                 }
  23.             } else {
  24.                 if (set.contains(c2)) {
  25.                     return false;
  26.                 }
  27.                 map.put(c1, c2);
  28.                 set.add(c2);
  29.             }
  30.         }
  32.         return true;
  33.     }

Longest Substring Without Repeating Characters

Given a string, find the length of the longest substring without repeating characters. For example, the longest substring without repeating letters for "abcabcbb" is "abc", which the length is 3. For "bbbbb" the longest substring is "b", with the length of 1.

  1.     public int lengthOfLongestSubstring(String s) {
  3.         if (s == null) {
  4.             return 0;
  5.         }
  7.         if (s.length() == 0 || s.length() == 1) {
  8.             return s.length();
  9.         }
  11.         char[] c = s.toCharArray();
  13.         int barrier = 0;
  14.         int maxLen = 1;
  16.         for (int i = 1; i < c.length; i++) {
  17.             for (int j = i - 1; j >= barrier; j--) {
  18.                 if (c[i] == c[j]) {
  19.                     barrier = j + 1;
  20.                     break;
  21.                 }
  22.             }
  23.             maxLen = Math.max(maxLen, i - barrier + 1);
  24.         }
  26.         return maxLen;
  27.     }

Repeated DNA Sequences

All DNA is composed of a series of nucleotides abbreviated as A, C, G, and T, for example: "ACGAATTCCG". When studying DNA, it is sometimes useful to identify repeated sequences within the DNA.

Write a function to find all the 10-letter-long sequences (substrings) that occur more than once in a DNA molecule.

For example,

Given s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT",

Return:
["AAAAACCCCC", "CCCCCAAAAA"].

考察位图。按位操作，A C G T分别用如下bits表示：

  1. A   00
  2. C   01
  3. G   10
  4. T   11

所以10个连续的字符，只需要20位即可表示，而一个int（32位）就可以表示。定义变量hash，后20位表示字符串序列，其余位数置0 。

定义一个set用来存放已经出现过的hash，计算新hash时，如果已经出现过，就放入结果的set中。

  1.     public List<String> findRepeatedDnaSequences(String s) {
  3.         if (s == null || s.length() < 11) {
  4.             return new ArrayList<String>();
  5.         }
  7.         int hash = 0;
  9.         Set<Integer> appear = new HashSet<Integer>();
  10.         Set<String> set = new HashSet<String>();
  12.         Map<Character, Integer> map = new HashMap<Character, Integer>();
  13.         map.put('A', 0);
  14.         map.put('C', 1);
  15.         map.put('G', 2);
  16.         map.put('T', 3);
  18.         for (int i = 0; i < s.length(); i++) {
  20.             char c = s.charAt(i);
  22.             hash = (hash << 2) + map.get(c);
  23.             hash &= (1 << 20) - 1;
  25.             if (i >= 9) {
  26.                 if (appear.contains(hash)) {
  27.                     set.add(s.substring(i - 9, i + 1));
  28.                 } else {
  29.                     appear.add(hash);
  30.                 }
  31.             }
  32.         }
  34.         return new ArrayList<String>(set);
  35.     }

Single Number

Given an array of integers, every element appears twice except for one. Find that single one.

Note:
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

对于出现2次的数字，用异或。因为“相异为1”，所以一个数字异或本身为0，而0异或0仍为0， 一个数字异或0仍为这个数字。

0 ^ 0 = 0 
n ^ 0 = n 
n ^ n = 0

  1.     public int singleNumber(int[] nums) {
  3.         int n = 0;
  5.         for (int i : nums) {
  6.             n ^= i;
  7.         }
  9.         return n;
  10.     }

Single Number II

Given an array of integers, every element appears three times except for one. Find that single one.

Note:
Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

对于数组{1,1,1,2}来说，分析每一位：

0 0 0 1 
0 0 0 1 
0 0 0 1 
0 0 1 0 
…………… 
0 0 1 3 (位数)

可以分析，分别计算每一位1的出现次数n，如果n%3==1，那么结果中这一位就应该是1。

  1.     public int singleNumber(int[] nums) {
  3.         int rt = 0, bit = 1;
  5.         for (int i = 0; i < 32; i++) {
  6.             int count = 0;
  8.             for (int v : nums) {
  9.                 if ((v & bit) != 0) {
  10.                     count++;
  11.                 }
  12.             }
  13.             bit <<= 1;
  14.             rt |= (count % 3) << i;
  15.         }
  17.         return rt;
  18.     }

Valid Anagram

Given two strings s and t, write a function to determine if t is an anagram of s.

For example,
s = "anagram", t = "nagaram", return true.
s = "rat", t = "car", return false.

Note:
You may assume the string contains only lowercase alphabets.

Follow up:
What if the inputs contain unicode characters? How would you adapt your solution to such case?

用数组模拟哈希表，统计字符出现次数。

  1.     public boolean isAnagram(String s, String t) {
  3.         if (s == null || t == null) {
  4.             return false;
  5.         }
  7.         if (s.length() != t.length()) {
  8.             return false;
  9.         }
  11.         if (s.equals(t)) {
  12.             return false;
  13.         }
  15.         int len = s.length();
  16.         int[] map = new int[26];
  18.         // 统计s中每个字符出现的次数
  19.         for (int i = 0; i < len; i++) {
  20.             map[s.charAt(i) - 'a']++;
  21.         }
  23.         // 减去t中相应字符出现次数
  24.         for (int i = 0; i < len; i++) {
  25.             map[t.charAt(i) - 'a']--;
  26.             if (map[t.charAt(i) - 'a'] < 0) {
  27.                 return false;
  28.             }
  29.         }
  31.         for (int i = 0; i < 26; i++) {
  32.             if (map[i] != 0) {
  33.                 return false;
  34.             }
  35.         }
  37.         return true;
  38.     }

Valid Sudoku

Determine if a Sudoku is valid, according to: Sudoku Puzzles - The Rules.

The Sudoku board could be partially filled, where empty cells are filled with the character '.'.

A partially filled sudoku which is valid.

Note:
A valid Sudoku board (partially filled) is not necessarily solvable. Only the filled cells need to be validated.

分别检查行、列、3*3方块。

  1.     public boolean isValidSudoku(char[][] board) {
  3.         if (board == null || board.length != 9 || board[0].length != 9) {
  4.             return false;
  5.         }
  7.         int mx = board.length;
  8.         int my = board[0].length;
  10.         // row
  11.         for (int x = 0; x < mx; x++) {
  12.             boolean[] flag = new boolean[10];
  13.             for (int y = 0; y < my; y++) {
  15.                 char c = board[x][y];
  16.                 if (c != '.') {
  17.                     if (flag[c - '0'] == false) {
  18.                         flag[c - '0'] = true;
  19.                     } else {
  20.                         return false;
  21.                     }
  22.                 }
  23.             }
  24.         }
  26.         // column
  27.         for (int y = 0; y < my; y++) {
  28.             boolean[] flag = new boolean[10];
  29.             for (int x = 0; x < mx; x++) {
  31.                 char c = board[x][y];
  32.                 if (c != '.') {
  33.                     if (flag[c - '0'] == false) {
  34.                         flag[c - '0'] = true;
  35.                     } else {
  36.                         return false;
  37.                     }
  38.                 }
  39.             }
  40.         }
  42.         // square
  43.         for (int x = 0; x < mx / 3; x++) {
  44.             for (int y = 0; y < my / 3; y++) {
  46.                 boolean[] flag = new boolean[10];
  48.                 for (int i = 0; i < 3; i++) {
  49.                     for (int j = 0; j < 3; j++) {
  51.                         char c = board[x * 3 + i][y * 3 + j];
  52.                         if (c != '.') {
  53.                             if (flag[c - '0'] == false) {
  54.                                 flag[c - '0'] = true;
  55.                             } else {
  56.                                 return false;
  57.                             }
  58.                         }
  59.                     }
  60.                 }
  61.             }
  62.         }
  64.         return true;
  65.     }

Word Pattern

Given a pattern and a string str, find if str follows the same pattern.

Here follow means a full match, such that there is a bijection between a letter in pattern and a non-empty word in str.

Examples:

  1. pattern = "abba", str = "dog cat cat dog" should return true.
  2. pattern = "abba", str = "dog cat cat fish" should return false.
  3. pattern = "aaaa", str = "dog cat cat dog" should return false.
  4. pattern = "abba", str = "dog dog dog dog" should return false.

Notes:
You may assume pattern contains only lowercase letters, and str contains lowercase letters separated by a single space.

Credits:
Special thanks to @minglotus6 for adding this problem and creating all test cases.

保证1对1的映射

  1.     public boolean wordPattern(String pattern, String str) {
  3.         if (pattern == null || str == null) {
  4.             return false;
  5.         }
  7.         String[] strs = str.split(" ");
  9.         if (pattern.length() != strs.length) {
  10.             return false;
  11.         }
  13.         Map<Character, String> map = new HashMap<Character, String>();
  15.         for (int i = 0; i < pattern.length(); i++) {
  17.             char c = pattern.charAt(i);
  19.             if (map.containsKey(c)) {
  20.                 if (!map.get(c).equals(strs[i])) {
  21.                     return false;
  22.                 }
  23.             } else {
  24.                 // 保证1对1的映射
  25.                 if (map.containsValue(strs[i])) {
  26.                     return false;
  27.                 }
  28.                 map.put(c, strs[i]);
  29.             }
  30.         }
  32.         return true;
  33.     }
添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注