LeetCode 动态规划 题目分类汇总

LeetCode

公众号

coding 笔记、点滴记录，以后的文章也会同步到公众号（Coding Insight）中，希望大家关注^_^

https://github.com/LjyYano/Thinking_in_Java_MindMapping

LeetCode解题链接

LeetCode 二叉树 题目分类汇总
干货！LeetCode 题解汇总

62. Unique Paths

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

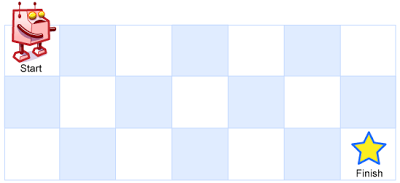
Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

思路

定义一个 m * n 的矩阵 dp，其中dp[m-1][n-1]代表从出发点(0, 0)→点(m, n)的路径个数。

• dp[i][0] = 1 (i∈[0, m))
• dp[0][j] = 1 (j∈[0, n))
• dp[m][n] = dp[m][n-1] + dp[m-1][n] (m > 0, n > 0)

优化

1. 在使用递归计算时，如果dp[m][n]计算过，就应该直接取出结果，而不是再次计算。实际中，可以将dp二维数组的初始值设置为-1，如果递归过程中，dp[m][n]!=-1，则表示计算过对应点的路径个数，直接返回结果。
2. 既然每一行，计算一次就没有用了，那么是否可以将空间复杂度降低？定义dp[m][n]的空间复杂度是m * n，如果只定义一个dp[m]，则可以将空间复杂度降低至m。

代码

利用递归，空间复杂度m * n：

public class Solution {
    public int robot(int m, int n, int[][] dp) {
        if(m == 0 || n == 0) {
            return 1;
        }
        if(dp[m][n] != -1) {
            return dp[m][n];
        }
        dp[m][n] = robot(m - 1, n, dp) + robot(m, n - 1, dp);
        return dp[m][n];
    }
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                dp[i][j] = -1;
            }
        }
        return robot(m - 1, n - 1, dp);
    }
}

迭代，空间复杂度m * n：

public int uniquePaths(int m, int n) {
    int[][] grid = new int[m][n];
    for(int i = 0; i<m; i++){
        for(int j = 0; j<n; j++){
            if(i==0||j==0)
                grid[i][j] = 1;
            else
                grid[i][j] = grid[i][j-1] + grid[i-1][j];
        }
    }
    return grid[m-1][n-1];
}

进一步优化，空间复杂度m：

public class Solution {
    public int uniquePaths(int m, int n) {
        int[] dp = new int[n];
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(i == 0 || j == 0)
                    dp[j] = 1;
                else if(j > 0)
                    dp[j] += dp[j - 1];
            }
        }
        return dp[n - 1];
    }
}

63. Unique Paths II

Follow up for "Unique Paths":

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

For example,
There is one obstacle in the middle of a 3x3 grid as illustrated below.

[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]

The total number of unique paths is 2.

Note: m and n will be at most 100.

思路

和上一题很像，只不过增加了一个限制条件：有些点可能不能走。不能走的点，dp变成0就好了。

代码

public class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int width = obstacleGrid[0].length;
        int[] dp = new int[width];
        dp[0] = 1;
        for(int[] row : obstacleGrid) {
            for(int j = 0; j < width; j++) {
                if(row[j] == 1) 
                    dp[j] = 0;
                else if(j > 0) 
                    dp[j] += dp[j - 1];
            }
        }
        return dp[width - 1];
    }
}

64. Minimum Path Sum

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

思路

定义一个二维数组sum[m][n]，表示从(0, 0)到(m - 1, n - 1)的最小的和。所以可以得出公式：

• sum[0][n] = grid[0][0] + grid[0][4] ... + grid[0][n]
• sum[m][0] = grid[0][0] + grid[1][0] ... + grid[m][0]
• sum[m][n] = min(sum[m - 1][n], sum[m][n - 1]) + grid[m][n]

sum[m - 1][n - 1] 即为最终结果。

代码

public class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] sum = new int[m][n];
        sum[0][0] = grid[0][0];
        for(int i = 1; i < m; i++) {
            sum[i][0] += sum[i - 1][0] + grid[i][0];
        }
        for(int j = 1; j < n; j++) {
            sum[0][j] += sum[0][j - 1] + grid[0][j];
        }
        for(int i = 1; i < m; i++) {
            for(int j = 1; j < n; j++) {
                sum[i][j] += Math.min(sum[i - 1][j], sum[i][j - 1]) + grid[i][j];
            }
        }
        return sum[m - 1][n - 1];
    }
}

53. Maximum Subarray

Find the contiguous subarray within an array (containing at least one number) which has the largest sum.

For example, given the array [-2,1,-3,4,-1,2,1,-5,4],
the contiguous subarray [4,-1,2,1] has the largest sum = 6.

思路

设数组sum[i]，其中sum[i]表示包括nums[i]的，nums数组从0~i的最大连续和。

• sum[i] = max(nums[i], sum[i - 1] + nums[i])
• max = max(sum[i], max)

以题干中的数组[-2,1,-3,4,-1,2,1,-5,4]为例，sum数组为：

[-2, 1, -2, 4, 3, 5, 6, 1, 5]

• 当i=0时，sum[0] = -2
• 当i=1时，sum1 = max(nums1, sum[0] + nums1) = max(1, -2 + 1) = 1
• ……

优化

sum[i]中的每一个数，都只会用到一次。所以可以将sum[i]数组，变成1个变量sum即可，sum的含义与sum[i]相同。

代码

public class Solution {
    public int maxSubArray(int[] nums) {
        if(nums.length == 0) return 0;
        int sum = nums[0], max = nums[0];
        for(int i = 1; i < nums.length; i++) {
            sum = Math.max(nums[i], sum + nums[i]);
            max = Math.max(sum, max);
        }
        return max;
    }
}

总结

对于动态规划的题目，最重要的一步就是写明递推公式和初始公式，缓存计算的中间结果，以获取效率。