LeetCode 307 Range Sum Query - Mutable

LeetCode

题目描述

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

The update(i, val) function modifies nums by updating the element at index i to val.

Example:

Given nums = [1, 3, 5]

sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8

Note:

1. The array is only modifiable by the update function.
2. You may assume the number of calls to update and sumRange function is distributed evenly.

分析

LeetCode 303 的数组是不可变的，本题的数组是可变的。可以使用树状数组，维基百科链接，不再具体介绍（不重复造轮子）。

树状数组(Fenwick_tree)，最早由Peter M. Fenwick于1994年以A New Data Structure for Cumulative Frequency Tables¹为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题，现多用于高效计算数列的前缀和。它可以以的时间得到，并同样以对某项加一个常数。

初始化复杂度最优为
单次询问复杂度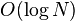,其中N为数组大小
单次修改复杂度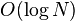,其中N为数组大小
空间复杂度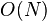

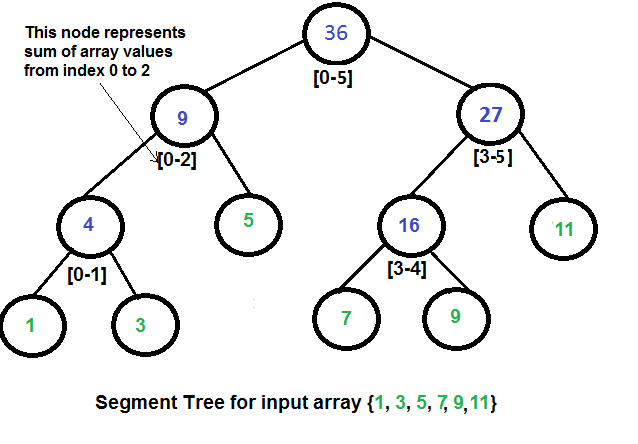
代码

public class NumArray {
    // array存储 nums数组，helper用来维护array的前缀和
    int[] array, helper;
    public NumArray(int[] nums) {
        array = new int[nums.length];
        helper = new int[nums.length + 1];
        for (int i = 0; i < nums.length; i++) {
            array[i] = nums[i];
        }
        for (int i = 0; i < nums.length; i++) {
            add(i + 1, nums[i]);
        }
    }
    private void add(int pos, int value) {
        while (pos < helper.length) {
            helper[pos] += value;
            pos += lowBit(pos);
        }
    }
    // 预备函数，返回参数转为二进制后,最后一个1的位置所代表的数值
    private int lowBit(int pos) {
        return pos & (-pos);
    }
    private int sum(int pos) {
        int rt = 0;
        while (pos > 0) {
            rt += helper[pos];
            pos -= lowBit(pos);
        }
        return rt;
    }
    void update(int i, int val) {
        int delta = val - array[i];
        array[i] = val;
        add(i + 1, delta);
    }
    public int sumRange(int i, int j) {
        return sum(j + 1) - sum(i);
    }
}