Java 八大排序实现

Java

参考链接

本文只给出算法的Java实现版本，具体原理参考：八大排序算法。

公用代码

下面的swap()函数，是排序算法中经常用到的，单独贴出来。

public void swap(int[] a, int i, int j) {
    int tmp = a[i];
    a[i] = a[j];
    a[j] = tmp;
}

冒泡排序

/**
 * 冒泡排序：每次循环，将最后一个位置排序好
 * 算法改进：加一个标志位，记录每趟排序最后一个进行交换的位置，下一次只需扫描到pos
 * @param a
 */
public void bubbleSort(int[] a) {
    if (a == null) {
        return;
    }
    int right = a.length - 1;
    while (right > 0) {
        int pos = 0;
        for (int start = 0; start < right; start++) {
            if (a[start] > a[start + 1]) {
                swap(a, start, start + 1);
                pos = start;
            }
        }
        right = pos;
    }
}

直接插入排序

将一个记录插入到已排序好的有序表中，从而得到一个新，记录数增1的有序表。即：先将序列的第1个记录看成是一个有序的子序列，然后从第2个记录逐个进行插入，直至整个序列有序为止。

public void insertSort(int[] a) {
    for (int right = 1; right < a.length; right++) {
        if (a[right] < a[right - 1]) {
            int tmp = a[right]; // 保存临时变量
            int left = right - 1;
            a[right] = a[right - 1]; // 先后移一个位置
            for (; left >= 0 && tmp < a[left]; left--) {
                a[left + 1] = a[left];
            }
            a[left + 1] = tmp;// 插入到正确位置
        }
    }
}

简单选择排序

1. 选出最小的元素，与数组第一个位置交换
2. 选出第i小的元素，与数组第i个位置交换
3. 直到第n-1个元素，与第n个元素比较为止

/**
 * 选择排序-简单选择排序
 * 基本思想：在一组要排序的数中，选取最小的与第一个位置交换
 */
public void selectSort(int[] a) {
    for(int start = 0; start < a.length; start++) {
        int key = selectMinKey(a, start);
        swap(a, key, start);
    }
}
private int selectMinKey(int[] a, int start) {
    int key = start;
    for(int i = start; i < a.length; i++) {
        key = a[key] > a[i] ? i : key;
    }
    return key;
}

快速排序

public void quickSort(int[] a) {
    quickSort0(a, 0, a.length - 1);
}
private void quickSort0(int[] a, int low, int high) {
    if (low < high) {
        int pos = partition(a, low, high);
        quickSort0(a, low, pos - 1);
        quickSort0(a, pos + 1, high);
    }
}
private int partition(int[] a, int low, int high) {
    int privotKey = a[low];
    while (low < high) {
        while (low < high && a[high] >= privotKey) {
            high--;
        }
        swap(a, low, high);
        while (low < high && a[low] <= privotKey) {
            low++;
        }
        swap(a, low, high);
    }
    return low;
}

归并排序

public void mergeSort(int[] a) {
    mergeSort0(a, 0, a.length - 1);
}
private void mergeSort0(int[] a, int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;
        mergeSort0(a, left, mid);
        mergeSort0(a, mid + 1, right);
        merge(a, left, mid, right);
    }
}
private void merge(int[] a, int start1, int mid, int right) {
    int[] tmp = new int[a.length];
    int k = start1; // tmp的初始下标
    int start = start1; // 记录初始位置
    int start2 = mid + 1; // 第2个数组的起始位置
    for(; start1 <= mid && start2 <= right; k++) {
        tmp[k] = a[start1] < a[start2] ? a[start1++] : a[start2++];
    }
    // 左边剩余的合并
    while (start1 <= mid) {
        tmp[k++] = a[start1++];
    }
    // 右边剩余的合并
    while (start2 <= right) {
        tmp[k++] = a[start2++];
    }
    // 复制数组
    while (start <= right) {
        a[start] = tmp[start];
        start++;
    }
}

堆排序

public void heapSort(int[] a) {
    buildingHeap(a, a.length);
    for (int i = a.length - 1; i > 0; i--) {
        swap(a, i, 0);
        adjustHeap(a, 0, i);
        System.out.println(Arrays.toString(a));
    }
}
/**
 * 选择排序-堆排序
 * 
 * 若以一维数组存储一个堆，则堆对应一个完全二叉树，且所有非叶结点的值，不大于其子女的值
 * 堆顶元素是最小的（小顶堆）
 *
 *
 * 已知a[s...m]除了a[s]外均满足堆的定义 调整a[s]，使之成为大顶堆，将第s个结点为根的子树筛选
 * 
 * a：待调整的堆数组 s：待调整的数组元素的位置 length：数组长度
 */
private void adjustHeap(int[] a, int s, int length) {
    int tmp = a[s];
    int child = 2 * s + 1; // 左孩子结点位置
    while (child < length) {
        // 如果有右孩子，同时右孩子值 > 左孩子值
        if (child + 1 < length && a[child] < a[child + 1])
            child++;
        if (a[s] < a[child]) { // 较大的子结点>父节点
            a[s] = a[child]; // 替换父节点
            s = child; // 重新设置，待调整的下一个结点位置
            child = 2 * s + 1;
        } else
            break;
        a[s] = tmp; // 交换
    }
}
/**
 * 初始堆进行调整 将a[0...length-1]建成堆
 * 调整完后，第一个元素是序列最小的元素
 */
private void buildingHeap(int[] a, int length) {
    // 最有一个有孩子结点的位置是 i = (length - 1) / 2
    for (int i = (length - 1) / 2; i >= 0; i--) {
        adjustHeap(a, i, length);
    }
}

测试用例

@Test
public void testHeapSort() {
    int[] a = new int[] { 4, 11, 5, 8, 1, 9, 2 };
    heapSort(a);
    System.out.println(Arrays.toString(a));
}

图解

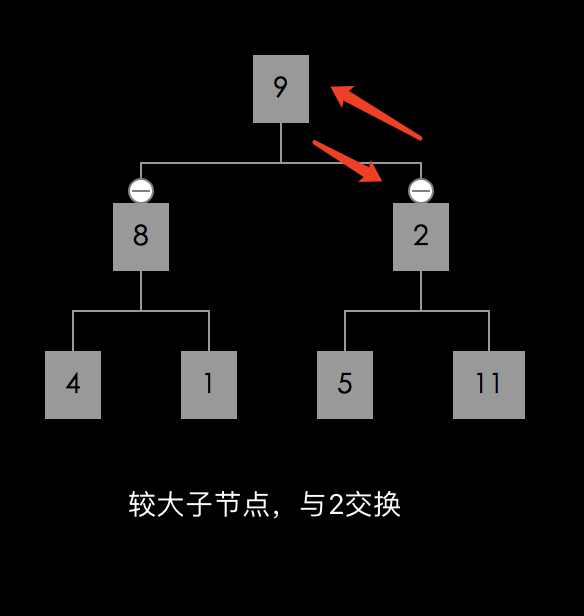
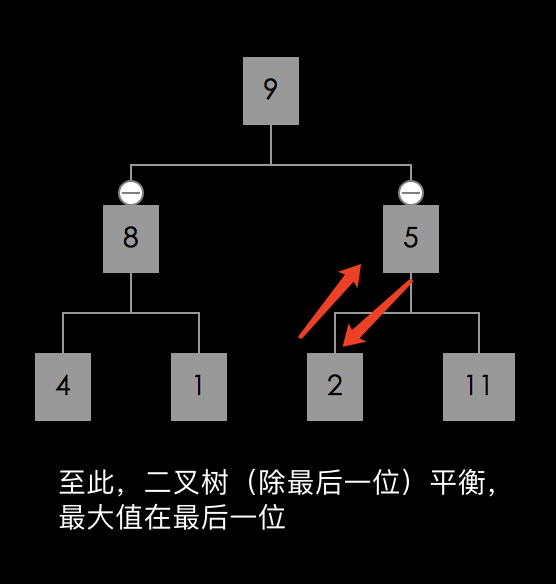
buildingHeap 后，形成了大顶堆。

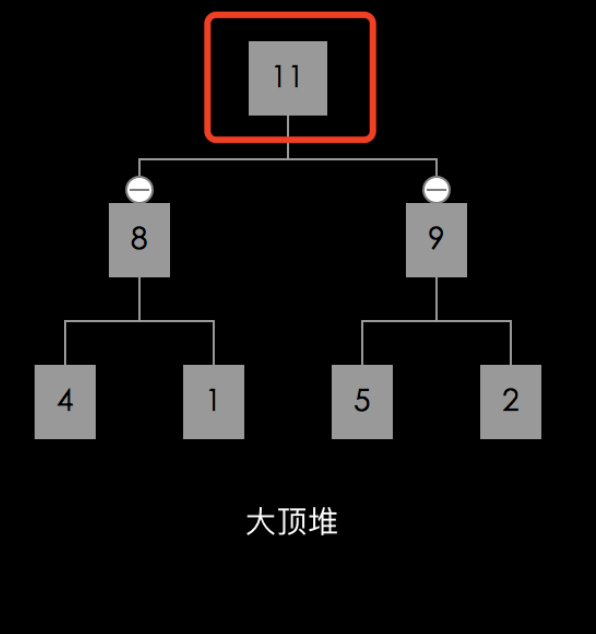
已经找到最大元素，与数组最后一个位置交换。

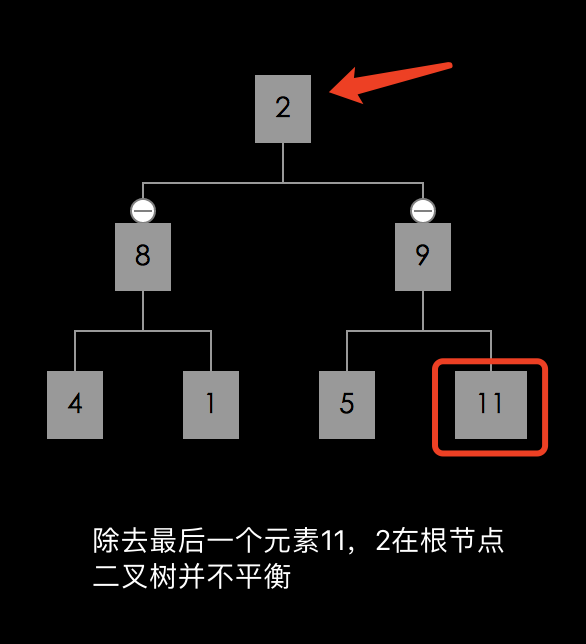
交换之后的二叉树并不平衡，需要调整。