第八次作业

作者：钟惠舟 班级：物基一班 学号：2013301020058

背景

　　本次作业简单对比了欧拉法与欧拉-克罗莫法的不同，并研究了单摆、阻尼摆及驱动摆的一些性质。

正文

1. 单摆
   　　对于单摆，在小角度摆动时，其运动方程可以写成： $$\frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta$$
   　　其解析解为：$\theta=\theta_0sin(\Omega t+\phi)$，式中$\Omega=\sqrt{g/l}$，$\theta_0$与$\phi$取决于单摆的初始状态。
   　　我们可以将此二阶方程写作两个一阶方程： $$\frac{d\omega}{dt}=-\frac{g}{l}\theta$$ $$\frac{d\theta}{dt}=\omega$$
   　　如果我们使用欧拉法，则： $$\omega_{i+1}=\omega_i-(g/l)\theta_i\Delta t$$ $$\theta_{i+1}=\theta_i+\omega_i\Delta t$$ $$t_{i+1}=t_i+\Delta t$$
   　　若使用欧拉-克拉默法，则： $$\omega_{i+1}=\omega_i-(g/l)\theta_i\Delta t$$ $$\theta_{i+1}=\theta_i+\omega_{i+1}\Delta t$$ $$t_{i+1}=t_i+\Delta t$$
   　　它们的区别仅仅在于用欧拉法时我们是用上一个$\omega$和上一个$\theta$来得到新的$\omega$和$\theta$；而用欧拉-克拉默法则是用上一个$\omega$和上一个$\theta$来得到新的$\omega$，再利用新的$\omega$来得到新的$\theta$。
   　　我们利用两种方法来获得单摆的摆角随时间的变化曲线。我们假设摆长为l=1m，初始角速度$\omega_0$=0rad/s，初始角度为$\theta_0=10^{\circ}$,时间间隔为$\Delta t$=0.01s,得到曲线图：
   　　　　　
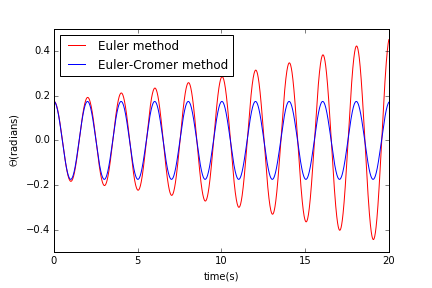
   　　由图我们可以看出，利用欧拉法得出的曲线与解析解并不符合，摆的振幅及能量都随着时间增加而增大，这显然不正确。而利用欧拉-克拉默法得到的曲线则不存在这样的问题。因此之后对摆的问题的处理我们采用的都是欧拉-克拉默法。
2. 阻尼摆
   　　对于阻尼摆，其运动方程形如： $$\frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta-q\frac{d\theta}{dt}$$
   　　式中($-q\frac{d\theta}{dt}$)项为阻尼项，q为阻尼系数。
   　　我们分三种情况讨论：
   　　1.欠阻尼状态
   　　这种状态下方程的解析解 $$\theta(t)=\theta_0e^{-qt/2}sin(\sqrt{\Omega^2-q^2/4}t+\phi)$$
   　　此时摆以频率$\sqrt{\Omega^2-q^2/4}$摆动，振幅随时间增大而减小。
   　　2.过阻尼状态
   　　此时方程的解析解为 $$\theta(t)=\theta_0e^{-(q/2\pm\sqrt{q^2/4-\Omega^2})t}$$
   　　摆角随时间增加而以指数形式单调递减。
   　　3.临界阻尼状态
   　　方程解析解形如 $$\theta(t)=(\theta_0+Ct)e^{-qt/2}$$
   利用欧拉-克拉默法可以得到三种情况下的$\theta-t$曲线，假设摆长为l=1m，初始角速度$\omega_0$=0rad/s，初始角度为$\theta_0=10^{\circ}$,时间间隔为$\Delta t$=0.01s：
   　　　
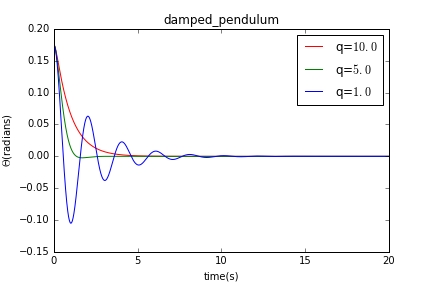
3. 驱动摆
   　　在阻尼摆的基础上加上驱动项得到驱动摆，驱动摆运动方程形如： $$\frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta-q\frac{d\theta}{dt}+F_Dsin(\Omega_D t)$$
   其中$F_Dsin(\Omega_D t)$为驱动项。
   　　我们研究驱动项对摆的影响。假设摆长为l=1m，初始角速度$\omega_0$=0rad/s，初始角度为$\theta_0=10^{\circ}$,时间间隔为$\Delta t$=0.01s，阻尼系数q=1.0。
   　　我们先使$\Omega_D=2.0$保持不变，分别使$F_D$等于0.2,0.6,1.0，得到曲线如下：
   　　　
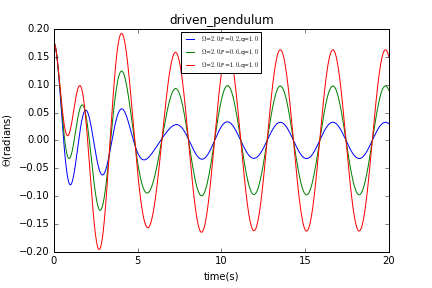
   　　然后我们使$F_D=0.2$保持不变，分别使$\Omega_D$等于1.0,2.0,3.0，得到曲线如下：
   　　　
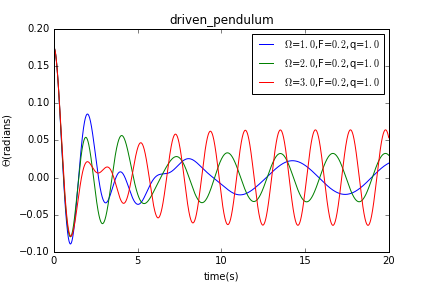
   　　上两种情况有一共同点，摆在经历一段不稳定的情况后均以稳定的振幅及频率摆动，相当于单摆的运动。当我们保持$\Omega_D$不变改变$F_D$时，不同$F_D$情况下摆在稳定摆动时的频率不变，振幅有明显差别；当我们保持$F_D$不变改变$\Omega_D$时，不同$\Omega_D$情况下摆在稳定摆动时的频率有明显区别，振幅大致相同。

总结

　　在研究摆的问题时，欧拉法近似不能使我们的问题得到解决，我们采取了新的近似方法：欧拉－克拉默方法。在单摆的基础上加上阻尼项，摆的振幅会不断变小直至停下来；在此基础上加上驱动项，摆在一段时间后会趋于稳定，形如单摆。

致谢

　　本次作业参照了教材，感谢蔡浩老师的教导。