第十四次作业

作者：钟惠舟 班级：物基一班 学号：2013301020058

背景

　　本次作业考察软绳上波的运动及波的频谱。
　　波的运动满足方程：

$$\frac{\partial^2y}{\partial t^2}=c^2 \frac{\partial^2y}{\partial x^2}$$
　　其中c是波速。要解出绳波的运动状态，必须给定一定的边界条件。常见的边界条件有自由边界条件和固定边界条件等。为简单起见，这里取固定边界条件，即绳端总是不发生横向位移。对于非端点的元段，则可以让其离散化，然后通过如下的迭代方法逐步求解绳波随时间的演化： $$y(i,n+1)=2[1-r^2]y(i,n)-y(i,n-1)+r^2[y(i+1,n)+y(i-1,n)]$$
　　这里$r=c\Delta t/\Delta x$。$t=n\Delta t$，$x=i\Delta x$分别是时间和元段位置坐标。初始条件通过如下方法给出：在连续两个时刻，给出绳波位移，这样即可开始迭代，给出绳波随时间的演化。
　　我们得到波的信号图之后，可以对信号做傅里叶分解，取模平方后得到频谱图。

正文

　　假设绳长1m，c=300m/s，$\Delta x=0.01m$,$\Delta t=\Delta x/c$,我们得到波的运动图：
　　
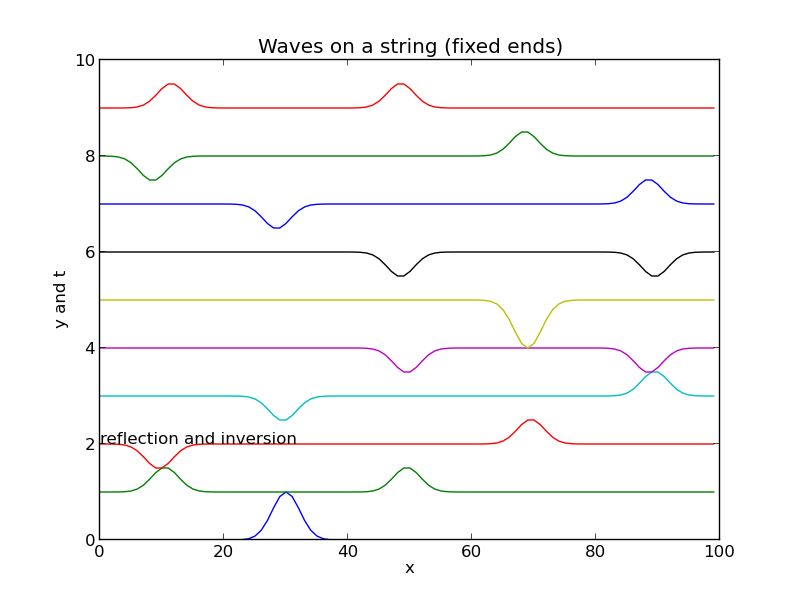
　　最上层两个波分别向两侧传播，反射后相遇再分离如此下去，由上往下表示随时间变化的结果。
　　我们还得到波的信号图及频谱图：
　　
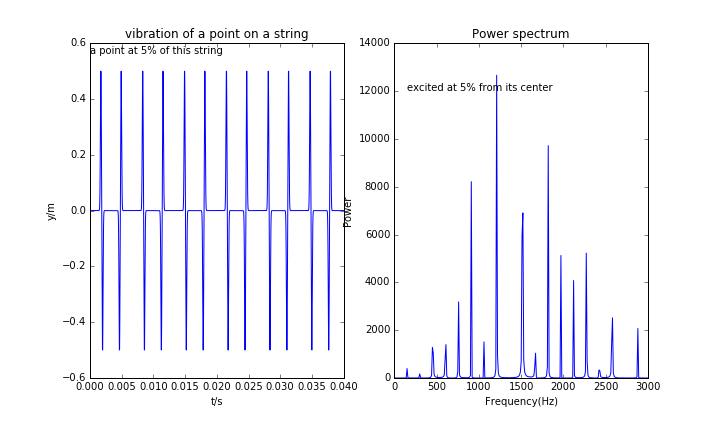
　　频率与波长之间存在关系：$\lambda f=c$,由于波长只允许为$\lambda=2L/m$，其中m为整数，因此频率只能取$mc/(2L)$。

结论

　　本次作业展示绳波的运动过程，并给出了在绳上给定点观察绳波信号的频谱。

致谢

　　感谢郭潇同学。