第九次作业

作者：钟惠舟 班级：物基一班 学号：2013301020058

背景

　　本次作业探讨了物理摆的一些规律及混沌现象的出现。

正文

　　我们在上次作业中讨论了摆在小角度时的一些现象及规律，现在我们不考虑小角度近似，并且考虑阻尼及驱动对摆的影响，我们得到摆的运动方程：

$$\frac{d^2\theta}{dt^2}=-\frac{g}{l}sin{\theta}-q\frac{d\theta}{dt}+F_Dsin(\Omega_D t)$$
　　我们同样可以把它写成两个一阶方程： $$\frac{d\omega}{dt}=-\frac{g}{l}sin{\theta}-q\frac{d\theta}{dt}+F_Dsin(\Omega_D t)$$ $$\frac{d\theta}{dt}=\omega$$
　　利用欧拉-克拉默计算法得到物理摆的$\theta -t$曲线，在计算时我们保证$\theta$一直处于$[-\pi,\pi]$之间。摆的一些常量为：l=g=9.8，q=0.5，$\Omega_D=2/3$，dt=0.04,$\theta_0$=0.2，$\omega_0$=0，单位为国际单位.
　　我们分别得到$F_D$等于0,0.5及1.2的$\theta -t$曲线：
　　　　
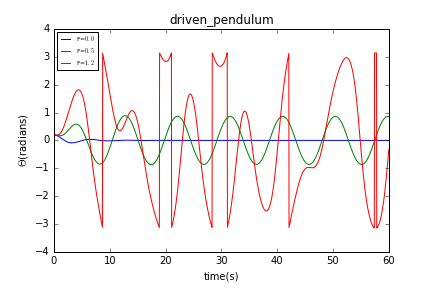
　　我们可以看到当$F_D$=0时，摆为阻尼摆，摆在一段时间后停止摆动。当$F_D$=0.5时，摆迅速进入稳定摆动状态。但是当$F_D$=1.2时，摆的运动变得毫无规律可言，这就是混沌行为。
　　我们从另一个角度看：假设有两个一模一样的摆，具有相同的长度及阻尼系数。它们唯一的区别在于摆的初始角度不一样。假设摆的常数同上，两摆初始角度相差0.001rad，得到$\Delta \theta=|\theta_1-\theta_2|$与时间的关系曲线：
　　
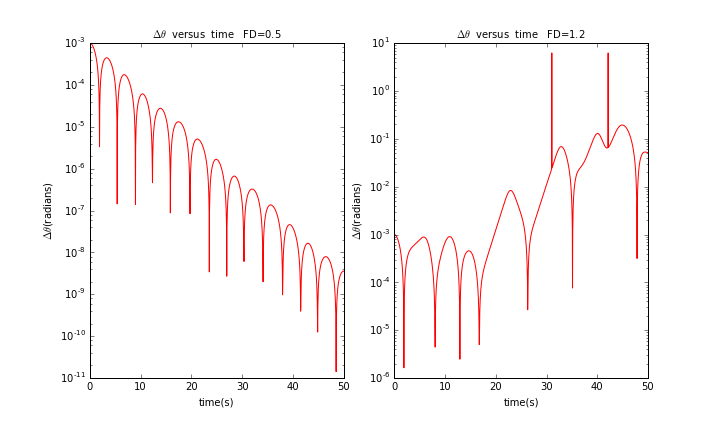
　　我们可以看到当$F_D$=0.5时，两摆的摆角差随时间的变化还是有规律可言的，$\Delta \theta$每过一定时间就会上升形成一个波峰，所有波峰的连线是一条趋势线，但当$F_D$=1.2时，情况再次变得难以预测。
　　上文提到的趋势线满足关系$\log(\Delta \theta)$正比于$\lambda t$,即$\Delta \theta \approx e^{\lambda t}$。
　　我们观察一下$\omega-\theta$曲线：
　　
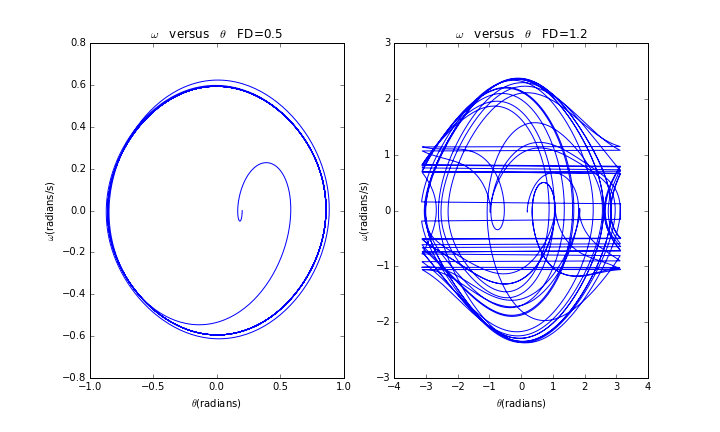
　　同样，在$F_D$=0.5时，$\omega-\theta$曲线最后趋近于一个椭圆，但当$F_D$=1.2时，曲线在此变得杂乱无章，出现混沌现象。
　　接下来我们仍然作$\omega-\theta$曲线，但是只画出满足条件$\Omega_D t=2n\pi$的点，即驱动项为零时的点，我们得到：
　　
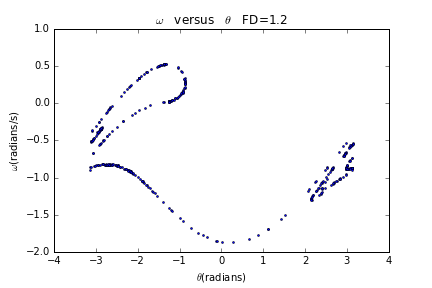
　　前面我们发现在$F_D$=1.2时摆出现混沌现象，那如果我们继续增大$F_D$会发生什么现象呢？我们得到当$F_D$分别等于1.35,1.44,1.465时的$\theta -t$曲线：
　　
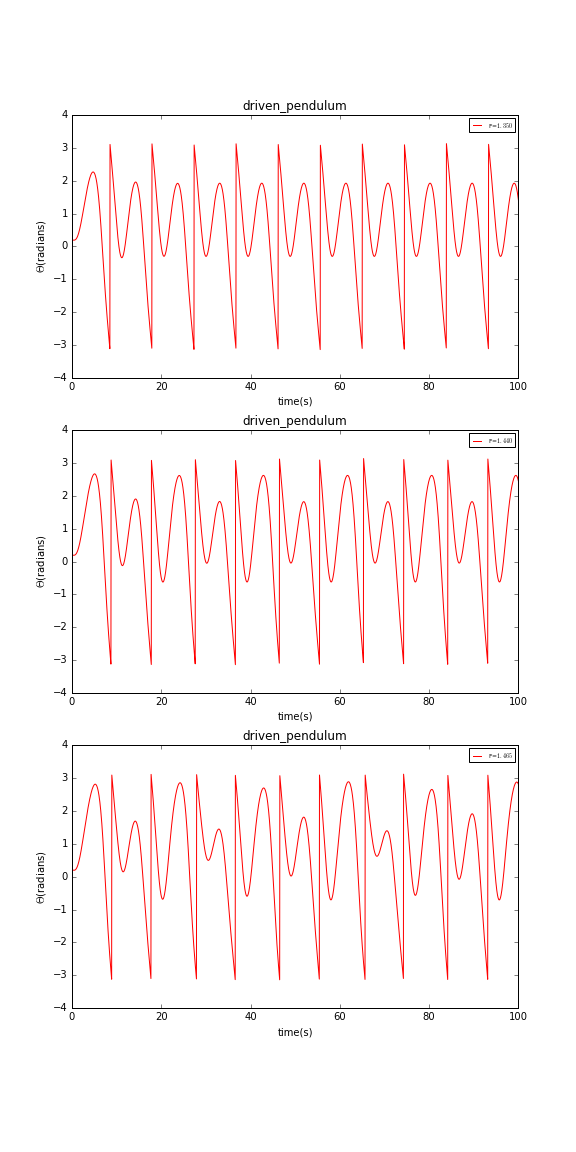
　　可以看到摆又变得有规律了。

总结

　　物理摆随驱动振幅$F_D$的变化，其规律性也发生变化，在一些$F_D$值物理摆会出现混沌现象。

致谢

　　本次作业参考了郭帅斐同学及陈洋遥同学的程序，在此表示感谢。