从单摆到混沌摆

作者：钟惠舟 学号：2013301020058 班级：物基一班

摘要

　　本文利用欧拉-克拉默法来探讨小角度($\theta <5^\circ$)下简单摆、阻尼摆及驱动摆的物理图像，并探讨了大角度下物理摆的规律及混沌现象的产生。

背景介绍

　　物体在一定位置附近作往复运动称为机械振动，简谐振动是振动的理想模型。由一根上端固定、不可伸缩且质量科忽略不计的细线和一个很重的小球所构成的振动系统称为单摆，在单摆的基础上增加非线性效应、阻尼及驱动力会使摆的运动变得复杂，甚至出现混沌现象。
　　庞加莱截面：庞加莱截面(Poincare surface of section)由Poincare于十九世纪末提出，用来对多变量自治系统的运动进行分析。其基本思想是在多维相空间中适当选取一截面，在此截面上某一对共扼变量取固定值，称此截面为Poincar截面。观测运动轨迹与此截面的截点( Poincare点)，设它们依次为P1,P2,P3…。原来相空间的连续轨迹在Poincare截面上便表现为一些离散点之间的映射Pn，由它们可得到关于运动特性的信息。如不考虑初始阶段的暂态过渡过程，只考虑Poincare截面的稳态图像，当Poincare截面上只有一个不动点和少数离散点时，可判定运动是周期的;当Poincare截面上是一封闭曲线时，可判定运动是准周期的;当Poincare截面上是成片的密集点，且有层次结构时，可判定运动处于混沌状态。

正文

一. 单摆

　　假设摆长为$l$，摆的角位移为$\theta$，我们可以得到摆的运动方程为

$$\frac{d^2\theta}{dt^2}=-\frac{g}{l}sin\theta$$
　　在小角度($\theta<5^\circ$)摆动时，数学我们有 $sin\theta \approx\theta$ ，故摆的运动方程可以写成： $$\frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta$$
　　其解析解为：$\theta=\theta_0sin(\Omega t+\phi)$，式中$\Omega=\sqrt{g/l}$，$\theta_0$与$\phi$取决于单摆的初始状态。由解析解我们知道单摆的运动应当随时间是正弦变化，是周期运动，下面我们利用计算法来得到摆的运动图像。
　　我们可以将此二阶方程写作两个一阶方程： $$\frac{d\omega}{dt}=-\frac{g}{l}\theta$$ $$\frac{d\theta}{dt}=\omega$$
　　使用欧拉-克拉默法，得到： $$\omega_{i+1}=\omega_i-(g/l)\theta_i\Delta t$$ $$\theta_{i+1}=\theta_i+\omega_{i+1}\Delta t$$ $$t_{i+1}=t_i+\Delta t$$
　　欧拉-克拉默法是用上一个$\omega$和上一个$\theta$来得到新的$\omega$，再利用新的$\omega$来得到新的$\theta$。
　　我们利用这种方法来获得单摆的摆角随时间的变化曲线。我们假设摆长为l=1m，初始角速度$\omega_0$=0rad/s，初始角度为$\theta_0=10^{\circ}$,时间间隔为$\Delta t$=0.01s,得到曲线图：
　　　　　
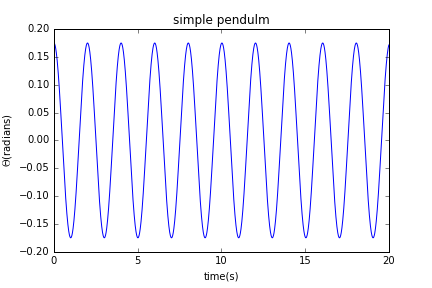
　　由图我们可以看出，摆角随时间作正弦函数变化，是严格的周期运动，这与我们用解析法得到的结果相符合。

二. 阻尼摆

　　在实际情况中，如果没有外力的维持，任何振动都会减幅。振幅随时间增加而减小的摆称为阻尼摆。
　　对于阻尼摆，其运动方程形如：

$$\frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta-q\frac{d\theta}{dt}$$
　　式中($-q\frac{d\theta}{dt}$)项为阻尼项，q为阻尼系数。
　　我们分三种情况讨论：
　　1.欠阻尼状态
　　这种状态下方程的解析解 $$\theta(t)=\theta_0e^{-qt/2}sin(\sqrt{\Omega^2-q^2/4}t+\phi)$$
　　此时摆以频率$\sqrt{\Omega^2-q^2/4}$摆动，振幅以指数形式随时间增大而减小。
　　2.过阻尼状态
　　此时方程的解析解为 $$\theta(t)=\theta_0e^{-(q/2\pm\sqrt{q^2/4-\Omega^2})t}$$
　　摆角随时间增加而以指数形式单调递减。
　　3.临界阻尼状态
　　方程解析解形如 $$\theta(t)=(\theta_0+Ct)e^{-qt/2}$$
利用欧拉-克拉默法可以得到三种情况下的$\theta-t$曲线，假设摆长为l=1m，初始角速度$\omega_0$=0rad/s，初始角度为$\theta_0=10^{\circ}$,时间间隔为$\Delta t$=0.01s：
　　　
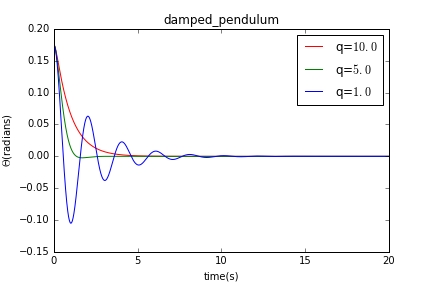
　　　可以看出由计算法得出的物理图像符合解析解。

三. 驱动摆

　　系统在周期性外力的持续作用下所发生的振动称为受迫振动。
　　在阻尼摆的基础上加上驱动项得到驱动摆，驱动摆运动方程形如：

$$\frac{d^2\theta}{dt^2}=-\frac{g}{l}\theta-q\frac{d\theta}{dt}+F_Dsin(\Omega_D t)$$
其中$F_Dsin(\Omega_D t)$为驱动项，$F_D$为驱动力的振幅。
　　我们研究驱动项对摆的影响。假设摆长为l=1m，初始角速度$\omega_0$=0rad/s，初始角度为$\theta_0=10^{\circ}$,时间间隔为$\Delta t$=0.01s，阻尼系数q=1.0。
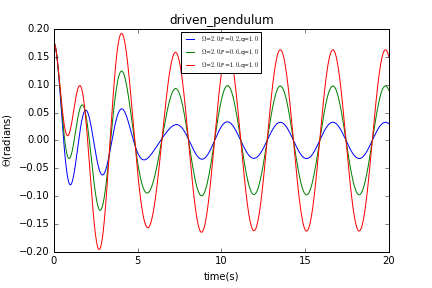
　　我们先使$\Omega_D=2.0$保持不变，分别使$F_D$等于0.2,0.6,1.0，得到曲线如下：
　　　
　　然后我们使$F_D=0.2$保持不变，分别使$\Omega_D$等于1.0,2.0,3.0，得到曲线如下：
　　　
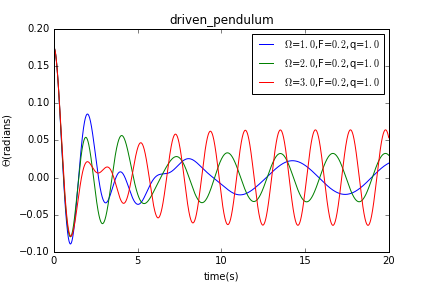
　　上两种情况有一共同点，摆在经历一段不稳定的情况后均以稳定的振幅及频率摆动，达到稳定的振动状态。当我们保持$\Omega_D$不变改变$F_D$时，不同$F_D$情况下摆在稳定摆动时的频率不变，振幅有明显差别；当我们保持$F_D$不变改变$\Omega_D$时，不同$\Omega_D$情况下摆在稳定摆动时的频率有明显区别，振幅大致相同。

四. 物理摆

　　上文中我们讨论了摆在小角度时的一些现象及规律，现在我们不考虑小角度近似，并且考虑阻尼及驱动对摆的影响，由此得到摆的运动方程：

$$\frac{d^2\theta}{dt^2}=-\frac{g}{l}sin{\theta}-q\frac{d\theta}{dt}+F_Dsin(\Omega_D t)$$
　　我们同样可以把它写成两个一阶方程： $$\frac{d\omega}{dt}=-\frac{g}{l}sin{\theta}-q\frac{d\theta}{dt}+F_Dsin(\Omega_D t)$$ $$\frac{d\theta}{dt}=\omega$$
　　利用欧拉-克拉默计算法得到物理摆的$\theta -t$曲线，在计算时我们保证$\theta$一直处于$[-\pi,\pi]$之间。摆的一些常量为：l=g=9.8，q=0.5，$\Omega_D=2/3$，dt=0.04，$\theta_0$=0.2，$\omega_0$=0，单位均为国际单位.
　　我们得到当$F_D$分别等于0，0.5及1.2时摆的$\theta -t$曲线：
　　　　
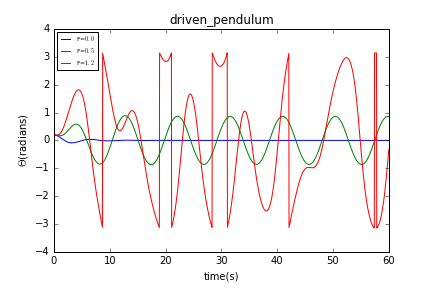
　　我们可以看到当$F_D$=0时，摆为阻尼摆，摆在一段时间后停止摆动。当$F_D$=0.5时，摆动由最初的暂态过渡到稳定的周期性摆动。但是当$F_D$=1.2时，摆的运动变得毫无规律可言，这就是混沌行为，这样的摆我们称之为混沌摆。

　　混沌摆对初值的敏感性

　　为进一步研究混沌摆的特征，我们考虑两个初值相差极小的近乎全同的摆，研究他们的的摆角差异。两个摆唯一的区别在于摆的初始角度不一样，假设摆的常数同上，两摆初始角度相差0.001rad，得到$\Delta \theta=|\theta_1-\theta_2|$与时间的关系曲线：
　　
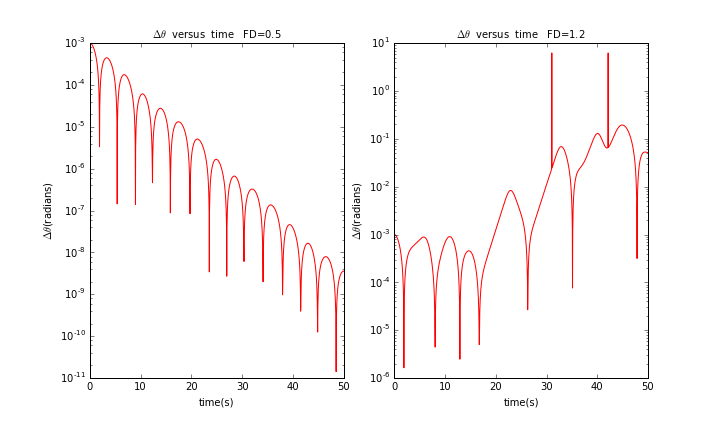
　　上文提到当$F_D$=0.5时摆最终会作稳定的周期运动，从上图我们可以再次看出$F_D$=0.5时摆的规律性。我们看到当$F_D$=0.5时两摆的摆角差随时间的变化是有规律的，$\Delta \theta$每过一定时间就会上升形成一个波峰，所有波峰的连线是一条趋势线趋势线满足关系$\Delta \theta \approx e^{\lambda t}$，总体上两者的角度差随时间增加而减小；但当$F_D$=1.2时，即我们认为是混沌摆时，两摆的角度差总体趋势为上升，但并无规律可言，这体现了混沌摆对初值具有极强的敏感性。

　　位形空间的相图

　　我们换一个角度观察混沌摆与非混沌摆的区别，$\omega-\theta$曲线即相图：
　　
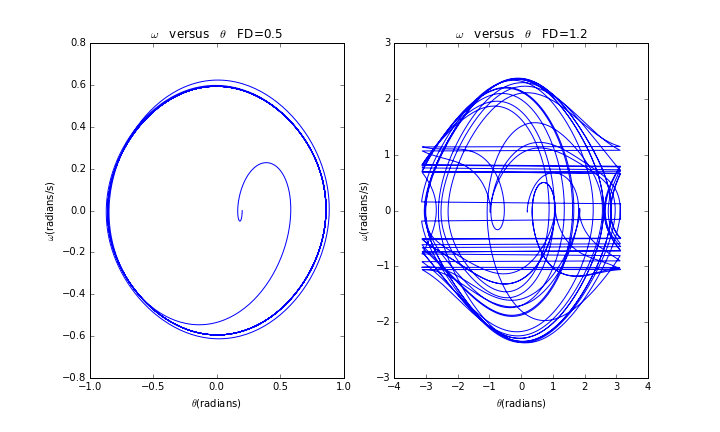
　　可以看到，非混沌摆($F_D$=0.5)的$\omega-\theta$曲线即相图除最初的暂态过程较复杂外，达到平衡后的相几乎是在同一个椭圆周上运行。而混沌摆($F_D$=1.2)的相图杂乱无章。
　　为进一步看到混沌运动的内禀特征，我们只取驱动力周期的整数倍时刻即$\Omega_D t=2n\pi$的点去观察摆的运动，把这些时刻的相画在相图上，得到所谓的庞加莱截面。我们得到：
　　
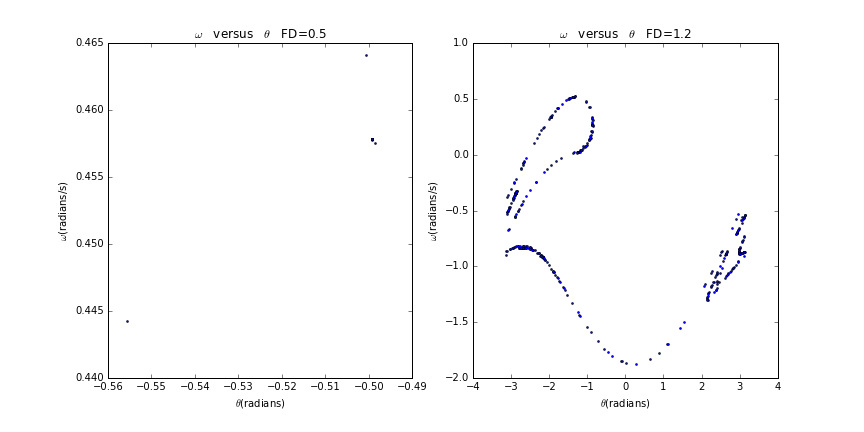
　　可以看到当$F_D$=0.5时庞加莱截面只有少数离散点，可判定此时摆的运动是周期的;当$F_D$=1.2时庞加莱截面上是成片的密集点，且有层次结构，可判定摆的运动处于混沌状态。

　　混沌产生机制

　　前面我们发现在$F_D$=0.5到$F_D$=1.2之间，摆由非混沌摆变成了混沌摆，我们希望了解摆转变的机制。由于这个区间段不能最清楚的展示这种机制，我们选择继续增大$F_D$来看看会发生什么现象。我们得到当$F_D$分别等于1.35，1.44，1.465时的$\theta -t$曲线：
　　
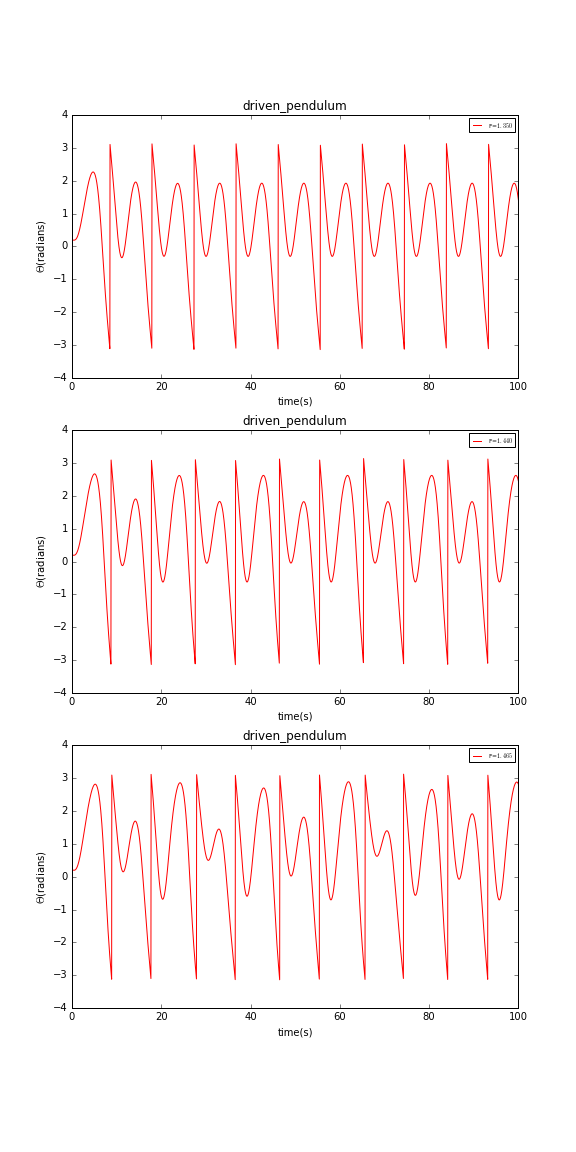
　　可以发现，这三种情况下的摆都还没有产生混沌现象，但是我们注意到$F_D$=1.35时摆的周期为驱动力周期，$F_D$=1.44时摆的周期为驱动力周期的两倍，$F_D$=1.465时摆的周期为驱动力周期的四倍，如果我们继续增大驱动力振幅$F_D$摆的周期会继续翻倍。如此下去，摆的周期将会无穷大，摆就会变成混沌摆，这就是混沌的产生机制之一:周期加倍。

结论

　　单摆运动是严格的周期运动，在其基础上增加了阻尼作用的阻尼摆是衰减摆。驱动摆的运动较复杂，很大程度上取决于驱动力振幅的大小。当驱动力振幅增大到一定值时，摆的运动出现混沌现象。

论文引用：

[1].计算物理(第二版),清华大学出版社
[2].经典力学(上册)，武汉大学出版社
[3].百度百科