计算物理第十二作业

计算物理

---

摘要

　　对电场的研究从来都是电磁学研究的重点，而通过电势来确定场的基本情况，是一种较为方便且常用的方法。本次作业将利用对空间中不同点的电势，来探讨不同边界条件下的电场情况，并回答课后习题5.1 5.4

背景

　　电场是电荷及变化磁场周围空间里存在的一种特殊物质。电场这种物质与通常的实物不同，它不是由分子原子所组成，但它是客观存在的，电场具有通常物质所具有的力和能量等客观属性。通常在图片中我们使用电场线来表示：
　　
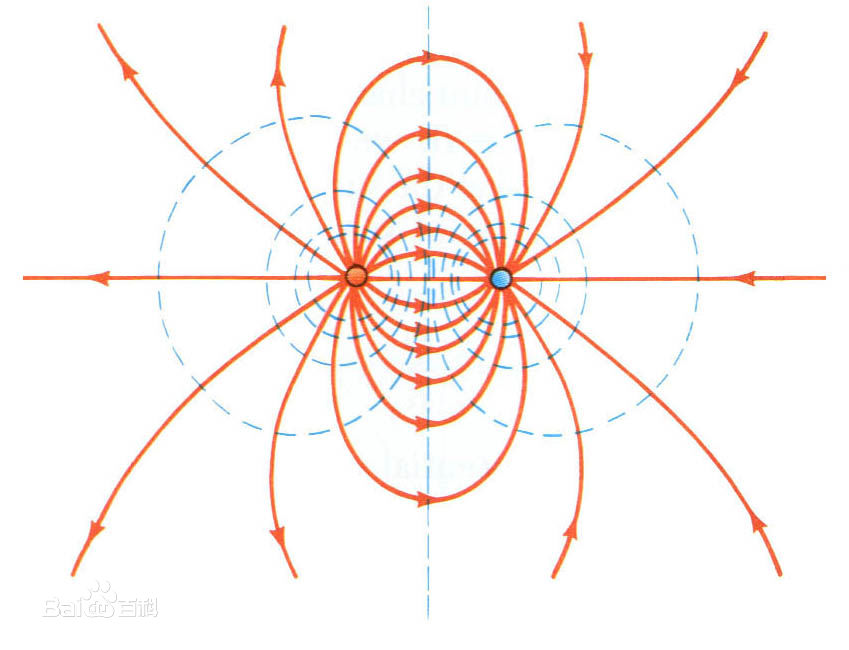
　　上图所示为正负点电荷之间的电场，其中橘红线表示电场线，浅蓝色线表示等势线。我们实际应用中会发现，对于电势的研究要比直接研究电场更为方便，因为电势是标量函数，只和空间位置有关，因此作图时我们亦可用等势线来描绘电场。
　　同时，电势的表示形式是多样的，除上图所示外，我们可以类比等高线做出下图：
　　
　　
　　
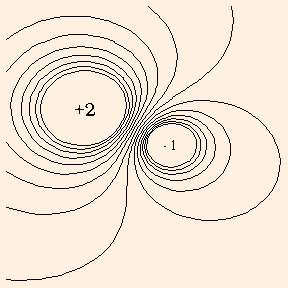
　　在这里我们将探究用这种图像来研究电场的方法。
　　首先对于电场的Laplace's equation
　　

$$\frac{\partial^2 V}{\partial x^2}+\frac{\partial^2 V}{\partial y^2}+\frac{\partial^2 V}{\partial z^2}=0$$
　　故而有：
$$\begin{eqnarray*} \frac{\partial V}{\partial x}&\approx&\frac{V(i+1,j,k)-V(i,j,k)}{\Delta x}\\ \frac{\partial V}{\partial x}&\approx&\frac{V(i,j,k)-V(i-1,j,k)}{\Delta x}\\ \frac{\partial V}{\partial x}&\approx&\frac{V(i+1,j,k)-V(i-1,j,k)}{2\Delta x}\\ \frac{\partial^2 V}{\partial x^2}&=&\frac{1}{\Delta x}[\frac{\partial V}{\partial x}(i+\frac12)-\frac{\partial V}{\partial x}(i-\frac12)]\\ &\approx&\frac{V(i+1,j,k)+V(i-1,j,k)-2V(i,j,k)}{(\Delta x)^2} \end{eqnarray*}$$
　　因此我们得到：
　　 $$V(i,j,k)=\frac16[V(i+1,j,k)+V(i-1,j,k)+V(i,j+1,k)-V(i,j-1,k)+V(i,j,k+1)-V(i,j,k-1)]$$
　　对于二维情况，有：
　　 $$V(i,j,k)=\frac14[V(i+1,j)+V(i-1,j)+V(i,j+1)-V(i,j-1)]$$
　　在此基础上，我们有 Jacobi Method
　　 $$V_{new}(i,j)=\frac{1}{4}[V_{old}(i+1,j)+V_{old}(i-1,j)+V_{old}(i,j+1)+V_{old}(i,j-1)]$$
　　我们亦可采用另一种计算方法，即Gauss-Sideal Method，可以更有效的减少内存占用率，且可以证明解的稳定性也不错
　　 $$V_{new}(i,j)=\frac{1}{4}[V_{old}(i+1,j)+V_{new}(i-1,j)+V_{old}(i,j+1)+V_{new}(i,j-1)]$$
　　除此之外还有Simulatneous over-relaxation(SOR) method，它可以很好地处理收敛速度相对较低的问题：
　　 $$\Delta V(i,j)=V^*(i,j)-V_{old}(i,j)$$
　　我们为了加速收敛，可以有
　　 $$V_{new}(i,j)=\alpha \Delta V^*(i,j)+V_{old}(i,j)$$
　　其中 $\alpha$ 可以衡量我们“放纵”收敛的程度，这里我们最好选择$\alpha \approx \frac{2}{1+\pi/L}$

正文

1. 无限大平板电容器

　　主程序如下：

from __future__ import division
import matplotlib
import numpy as np
import matplotlib.cm as cm
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from copy import deepcopy
# initialize the grid
grid = []
for i in range(201):    
    row_i = []
    for j in range(201):
        if i == 0 or i == 200 or j == 0 or j == 200:
            voltage = 0
        elif 50<=j<=51 :
            voltage = 1
        elif 150<=j<=151 :
            voltage = -1
        else:
            voltage = 0
        row_i.append(voltage)
    grid.append(row_i)
# define the update_V function (Gauss-Seidel method)
def update_V(grid):
    delta_V = 0
    for i in range(201):    
        for j in range(201):
            if i == 0 or i == 200 or j == 0 or j == 200:
                pass
            elif 50<=j<=51 :
                voltage = 1
            elif 150<=j<=151 :
                voltage = -1
            else:
                voltage_new = (grid[i+1][j]+grid[i-1][j]+grid[i][j+1]+grid[i][j-1])/4
                voltage_old = grid[i][j]
                delta_V += abs(voltage_new - voltage_old)
                grid[i][j] = voltage_new
    return grid, delta_V
# define the Laplace_calculate function
def Laplace_calculate(grid):
    epsilon = 10**(-5)*200**2
    grid_init = grid
    delta_V = 0
    N_iter = 0
    while delta_V >= epsilon or N_iter <= 10:
        grid_impr, delta_V = update_V(grid_init)
        grid_new, delta_V = update_V(grid_impr)
        grid_init = grid_new
        N_iter += 1
    return grid_new
x = np.linspace(0,200,201)
y = np.linspace(0,200,201)
X, Y = np.meshgrid(x, y)
Z = Laplace_calculate(grid)
Ex = deepcopy(Z)
Ey = deepcopy(Z)
E = deepcopy(Z)
for i in range(201):
    for j in range(201):
        if i == 0 or i == 200 or j == 0 or j == 200:
            Ex[i][j] = 0
            Ey[i][j] = 0
        else:
            Ex_value = -(Z[i+1][j] - Z[i][j])/2
            Ey_value = -(Z[i][j+1] - Z[i][j])/2
            Ex[i][j] = Ex_value
            Ey[i][j] = Ey_value
for i in range(201):
    for j in range(201):
        E_value = np.sqrt(Ex[i][j]**2 + Ey[i][j]**2)
        E[i][j] = E_value
fig0, ax0 = plt.subplots()
strm = ax0.streamplot(X, Y, np.array(Ey), np.array(Ex), color=np.array(E), linewidth=2, cmap=plt.cm.autumn)
ax0.set_xlabel('x(m)')
ax0.set_ylabel('y(m)')
ax0.set_title('Electric field')
plt.show()

结论

1. 两带电平板

1.1

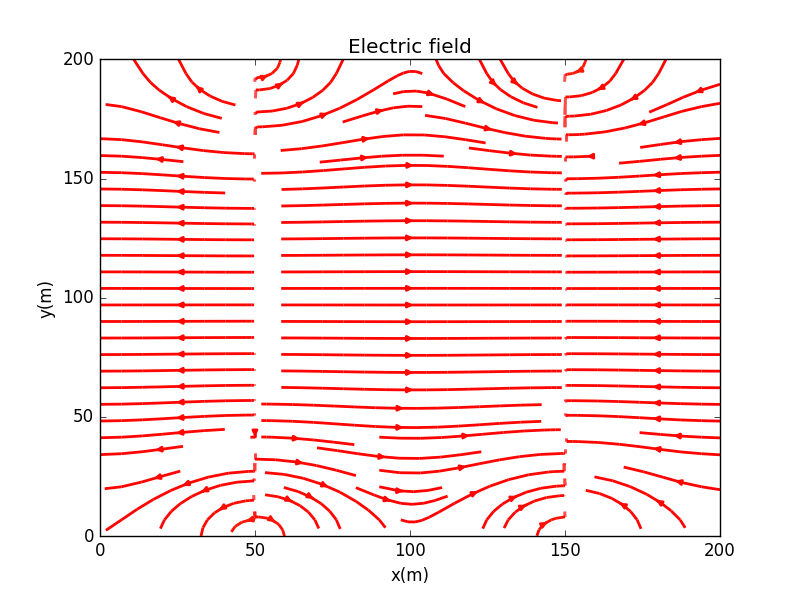
可见在两板内部的确近似为匀强电场
我们可以改变平板带点属性，改为两板有相同电势

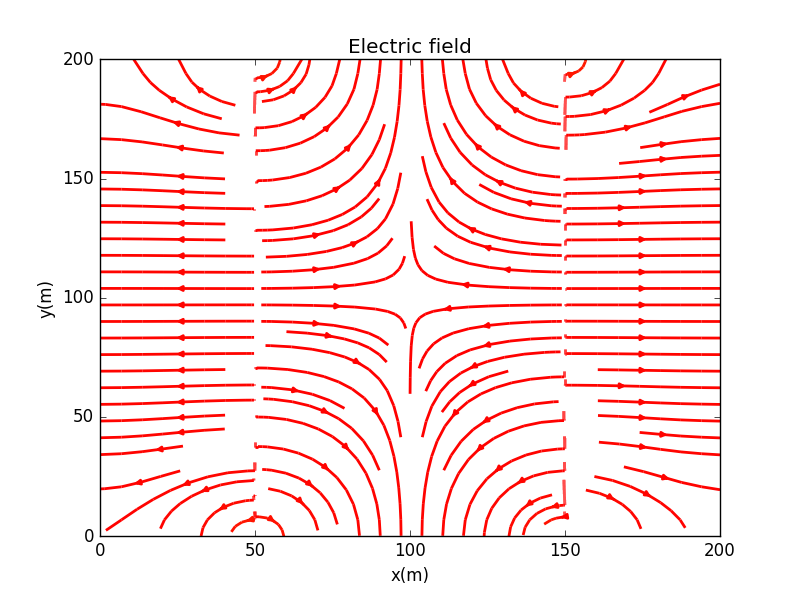
1.2

若我们考虑Figure 5.6的边界条件，可进一步研究作图如下：

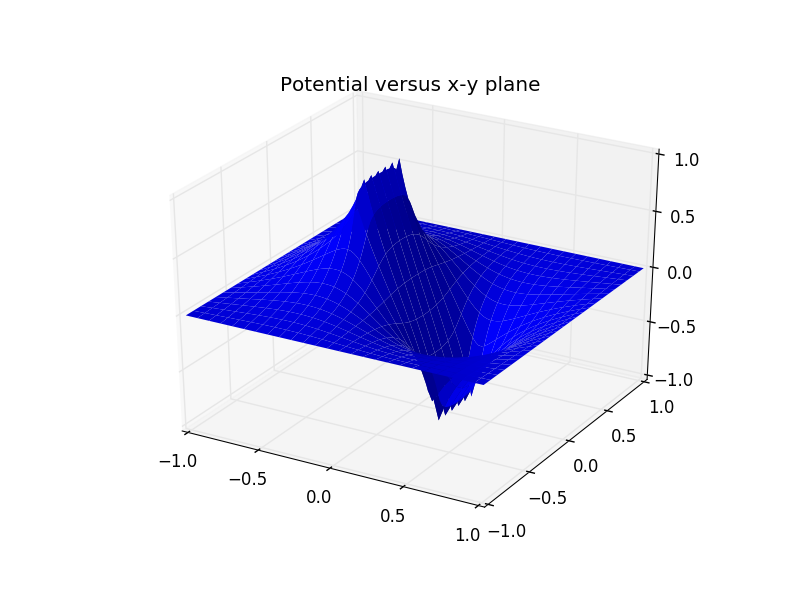
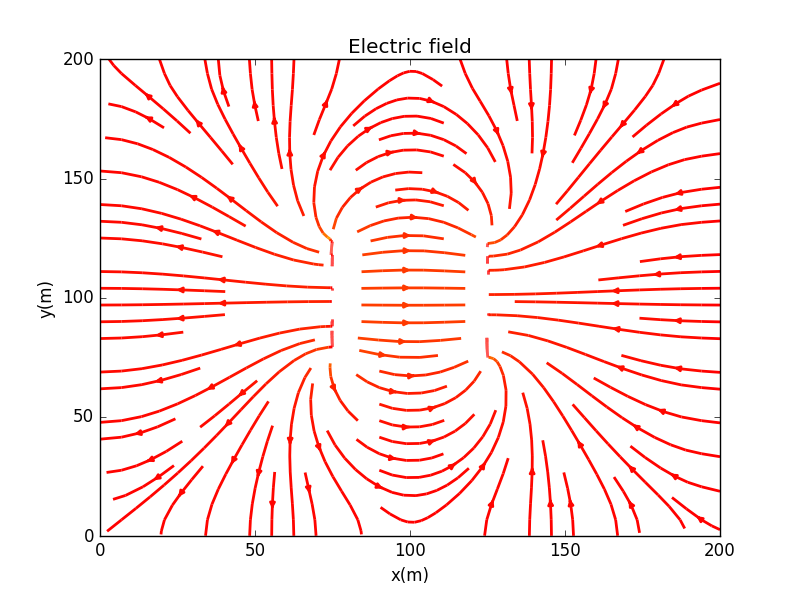
2. 正方形平板与有边界情况

　　这里我们取Figure 5.4的边界条件，即：

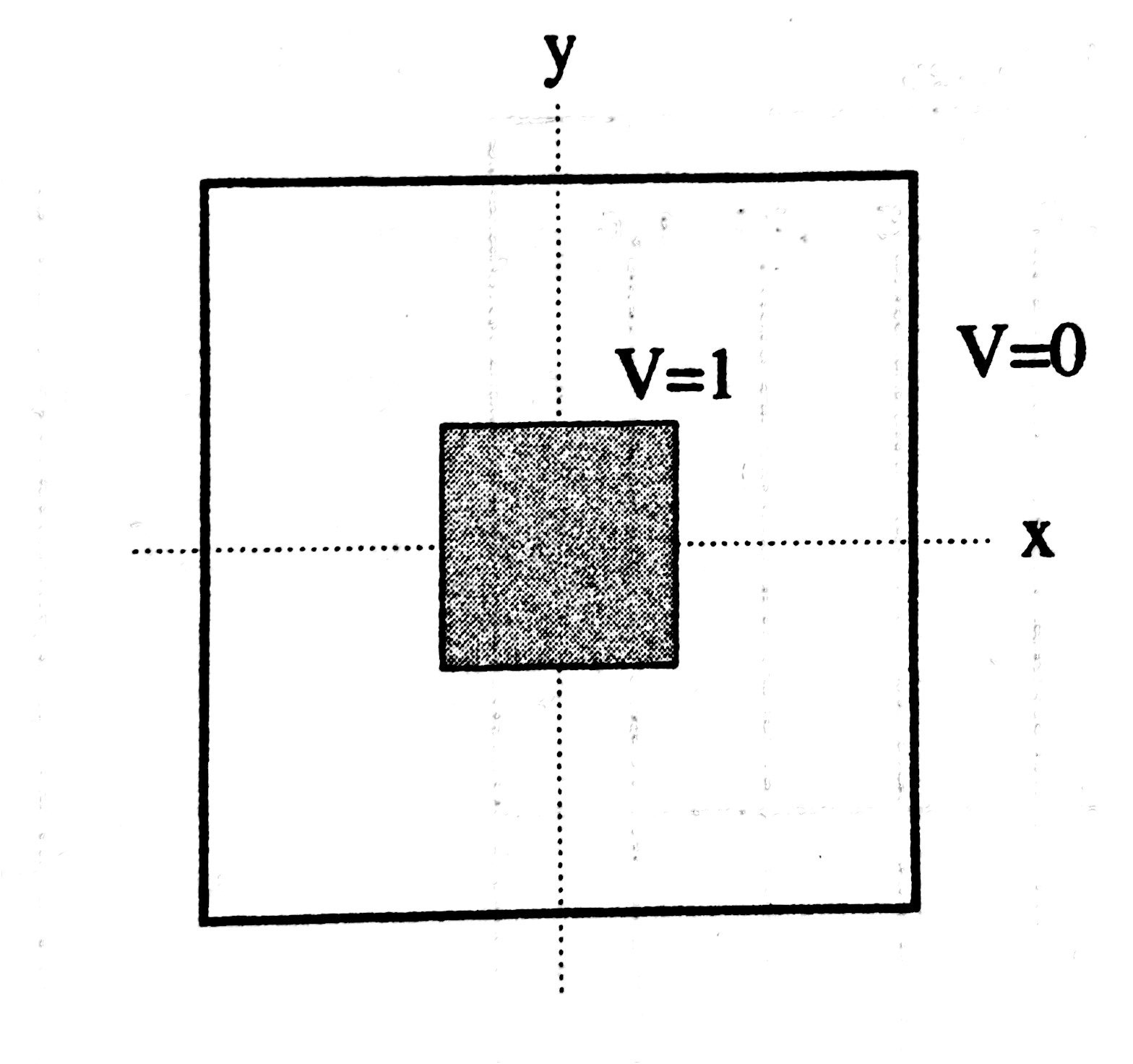
　　此时可得到图像：
　　
　　
　　

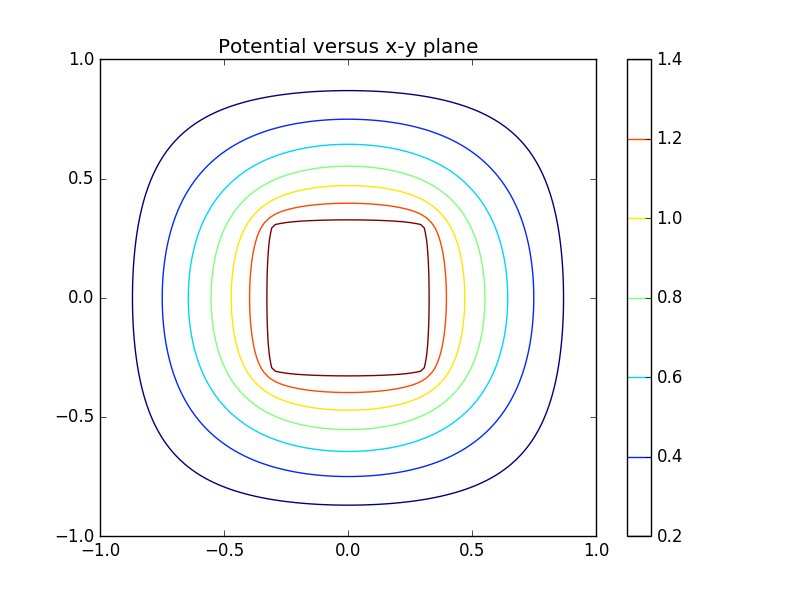
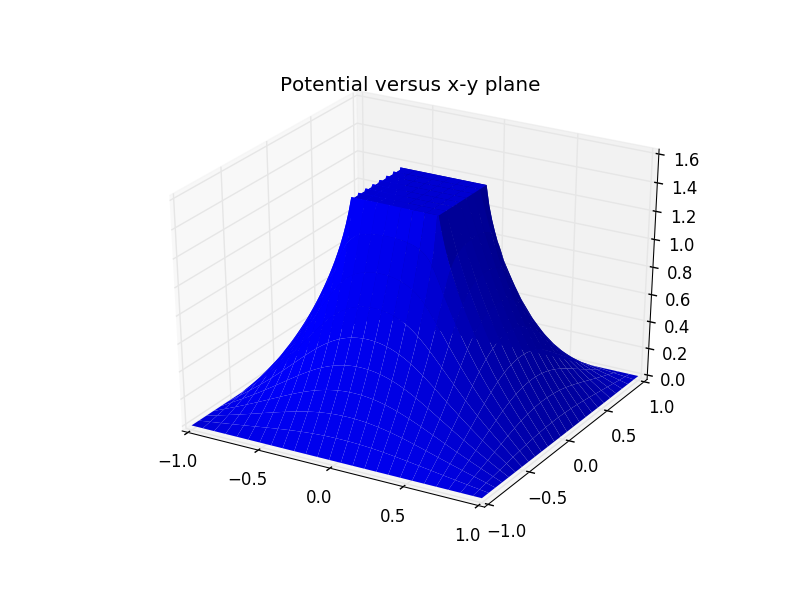
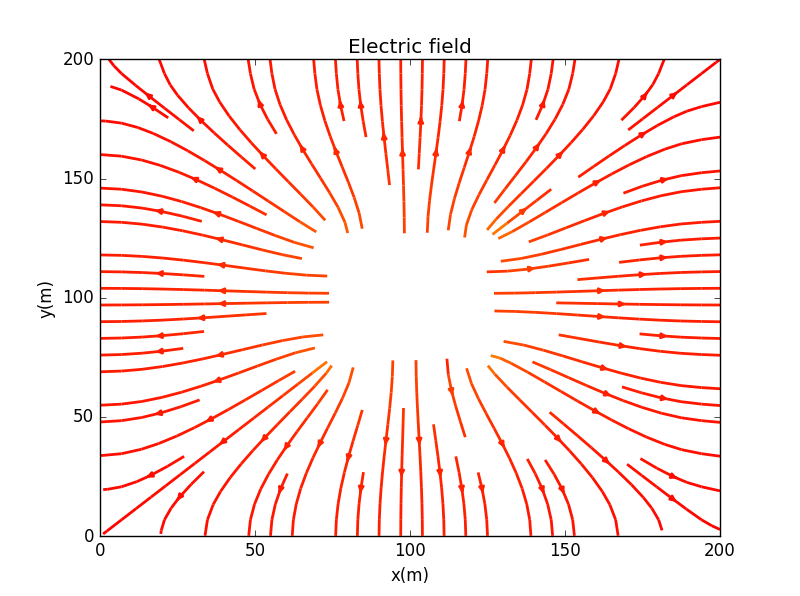
3. 点电荷

　　这里我们仍然设定外边界的电势为零，同时为了对比方便，我们这次将3D图和等势线图合并，改变相应参数可得如下图像
　　
　　

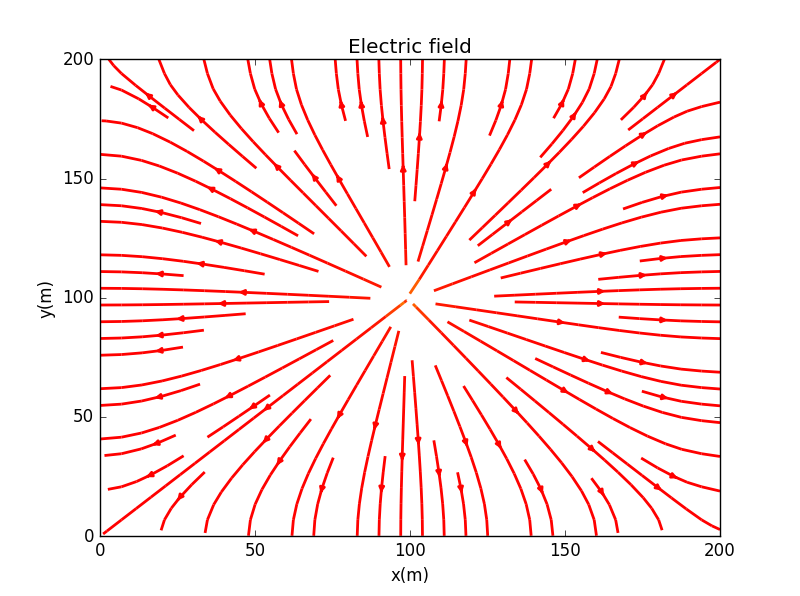
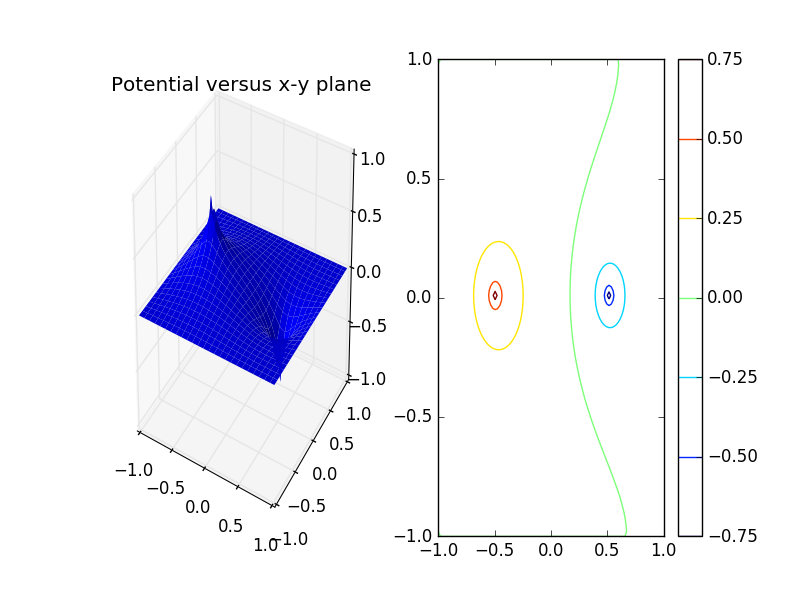
4. 两个点电荷

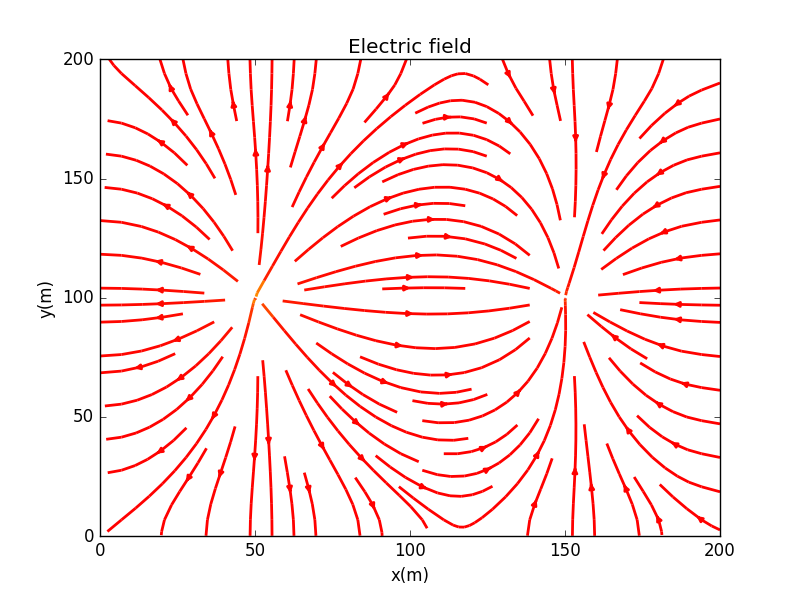
致谢

张梓桐同学的帮助