第六讲 爱上统计学

樊潇彦 复旦大学经济学院 经济数学

1. 课件和资料

Ch06.pdf1873.2kB

2. 程序附录

2.1 概率函数

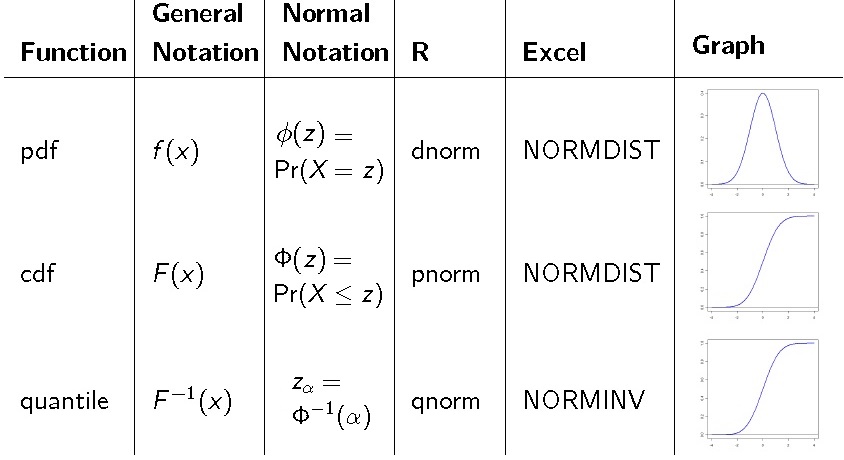
四种前缀（以正态分布 $x\text{～} N\left(\mu,\sigma^2\right)$ 为例）：

• d: 概率密度函数或频率函数dnorm(x,mu,sigma)
• p: 累积分布函数pnorm(x,mu,sigma)
• q: 给定概率 $\alpha$，求累积分布的右侧分位点qnorm(1-alpha/2,mu,sigma)
• r: 生成随机数rnorm(N,mu,sigma)

x <- seq(from = -5, to = 5, by = 0.01)
y <- dnorm(x)
plot(x=x,y=y,type="l",col="seagreen",lwd=2,
  xlab="x",ylab="density\ny = dnorm(x)")
grid(col="darkgrey",lwd=2)
title(main="概率分布(PDF)")
y <- pnorm(x)
plot(x=x,y=y,type="l",col="seagreen",lwd=2, xlab="x = qnorm(y)",
   ylab="probability\ny = pnorm(x)")  ; grid(col="darkgrey",lwd=2)
title(main="累积分布(CDF)")
set.seed(1)
x <- rnorm(100, sd=3)                            # 模拟生成单变量
y <- rnorm(100, mean=1) + x
mn = apply(cbind(x,y), 2, mean)                  # 计算x和y的均值
covmat= cov(cbind(x,y))                          # 计算x和y的协方差
library(mnormt)                                  # 调用生成多元随机变量的包
simdata=rmnorm(300,mean=mn,varcov=covmat)        # 模拟生成双变量
library(ggplot2)
ggplot(as.data.frame(simdata), aes(x=x, y=y)) +
  geom_point() +
  geom_smooth(method="lm") +
  theme_bw()

2.2 统计描述：以汽车保险数据为例

• 常用指标一览
  

library(MASS)
data(Insurance)                                  # 调用保险数据
str(Insurance)                                   # 查看数据结构
attach(Insurance)                                # 绑定数据

• 单变量统计描述

# 1）连续变量
mean(Holders)                                    # 基本统计量，不能有缺失值
# mean(Holders, na.rm = TRUE)                    # 有缺失值时用
median(Holders)
sd(Holders)
var(Holders)
quantile(Holders)                                # 四分位值
quantile(Holders,seq(0,1,0.1))                   # 十分位值
library(Hmisc)
describe(data.frame(District, Group, Age))       # 简单数据描述
describe(data.frame(Holders, Claims))
library(fBasics)
basicStats(data.frame(Holders, Claims))          # 更多统计量 
# 2）离散变量
table(Age)                                       # 离散变量频率表

• 双变量统计描述

# 1）两个连续变量
cor(data.frame(Holders, Claims),use="pairwise",method="pearson") # 相关系数
cov(data.frame(Holders, Claims),use="pairwise",method="pearson") # 协方差矩阵
# 2）一个连续变量和一个离散变量
by(data.frame(Holders,Claims),Age,summary)       # 按离散变量分组，对连续变量做统计描述
# 3）两个离散变量
table(District,Age)                              # 两个离散变量频率表
detach(Insurance)                                # 解除绑定

2.3 统计推断：以资产收益率数据为例

• 参数检验
  
  • 正态分布 $X\text{～}N\left(\mu,\sigma^2\right)$
    
    • 均值检验（$\sigma^2$ 未知）t.text()：单变量 $H_0:\mu=\mu_0$，双变量 $H_0:\mu_1=\mu_2$
    • 方差检验（$\mu$ 未知）：var.text()：单变量 $H_0:\sigma^2=\sigma^2_0$，双变量 $H_0:\sigma^2_1=\sigma^2_2$
  • 总体分布未知，单变量或双变量均值检验：wilcox.test()
• 分布检验：单变量 $H_0:X\text{～}F\left(x\right)$，双变量 $H_0:F_1\left(x\right)=F_2\left(x\right)$
  
  • Jarque-Bera $JB$ 检验 normalTest()
  • Pearson $\chi^2$ 检验 chisq.test()
  • Kolmogorov-Smirnov检验 ks.test()

# 以Tsay(2013)中3M公司股票对数收益率为例
url="https://faculty.chicagobooth.edu/ruey.tsay/teaching/introTS/ch1data.zip"
download.file(url, "ch1data.zip")                           # 下载存为同名文件
x=read.table(unz("ch1data.zip","d-mmm-0111.txt"),header=T)  # 读入数据
x=x[,2]                                                     # 去掉日期
# 1) 作图                  
hist(x,nclass=30)                                           # 直方图
d1=density(x,na.rm=T)                                       # 密度
plot(d1$x,d1$y,xlab='',ylab='',type='l',
     main="3M公司股票对数收益率密度函数")                   # 画密度线
rangex=range(x,na.rm=T)                                     # 取值范围
seqx=seq(rangex[1],rangex[2],.001)                          # x轴间隔0.001
y1=dnorm(seqx,mean(x,na.rm=T),stdev(x,na.rm=T))             # 正态分布
lines(seqx,y1,lty=2)                                        # 添加正态分布线
# 2) 检验
basicStats(x) 
mean(x,na.rm=TRUE); var(x,na.rm=TRUE); stdev(x,na.rm=TRUE); 
t.test(x)                                                   # 均值检验 H0: x=0 
normalTest(x,method='jb',na.rm=T)                           # 正态分布检验，JB-test
s3=skewness(x,na.rm =T)
T=length(x) 
t3=s3/sqrt(6/T)                     
pp=2*(1-pnorm(t3))                                          # 偏度检验(Skewness test)
s4=kurtosis(x,na.rm =T)
t4=s4/sqrt(24/T) 
pp=2*(1-pnorm(t4))                                          # 峰度检验(Kurtosis test)

3. 推荐阅读