四、动态最优（II）最优控制方法

樊潇彦 复旦大学经济学院 数量经济学

---

0. 准备工作

setwd("D:\\...")   # 设定工作目录
rm(list=ls())      # 清内存
# "Ctrl"+"L" 清除命令窗口
library(ggplot2)
library(nleqslv)

对于连续时间的最优增长问题：

$$\begin{array}{*{20}{l}} {\max \int_{t = 0}^\infty {{e^{ - \rho t}}u\left( c \right)dt} }\\ {s.t.~\dot k = f\left( k \right) - c - \delta k}\\ ~~~~~~~~{k\left( 0 \right) = 1,~~\mathop {lim}\limits_{t \to \infty } {e^{ - \rho t}}u'\left( c \right)k = 0} \end{array}$$
写出汉密尔顿函数：
$$H = {e^{ - \rho t}}u\left( c \right) + \lambda \left[ {f\left( k \right) - c - \delta k} \right]$$
根据最大值原理有：
$$\begin{array}{l} \frac{{\partial H}}{{\partial c}} = {e^{ - \rho t}}u'\left( c \right) - \lambda =0\\ \frac{{\partial H}}{{\partial k}} = \lambda \left[ {f'\left( k \right) - \delta } \right] = - \dot \lambda \\ \frac{{\partial H}}{{\partial \lambda }} = f\left( k \right) - c - \delta k\\ \lambda \left( 0 \right)k\left( 0 \right) = \mathop {\lim }\limits_{t \to \infty } \lambda k = 0 \end{array}$$
前两个条件合并得到：
$$\begin{array}{l} {e^{ - \rho t}}u'\left( c \right)\left[ {f'\left( k \right) - \delta } \right] = - {e^{ - \rho t}}\left[ { - \rho u'\left( c \right) + u''\left( c \right)\dot c} \right]\\ \Rightarrow \dot c = - \frac{{u'\left( c \right)}}{{u''\left( c \right)}}\left[ {f'\left( k \right) - \delta - \rho } \right] \end{array}$$

1. 设定参数

rho <- 0.03                                            # 贴现因子
gamma <- 1                                             # 效用函数
if (gamma==1){u.fmla <- expression(log(c))
              }else{
  u.fmla <- expression(c^(1-gamma)/(1-gamma))}
alpha <- 0.5                                           # 生产函数
f.fmla <- expression(k^alpha)
delta <- 0.1                                           # 折旧率

2. 微分方程组与稳态

d2u.fmla <- deriv3(u.fmla,"c","c")                     # 效用函数求导
u <- function(c) { eval(u.fmla) }                              # u
du <- function(c) { as.vector(attr(d2u.fmla(c),"gradient")) }  # u'
d2u <- function(c) { as.vector(attr(d2u.fmla(c),"hessian")) }  # u"
df.fmla <- deriv(f.fmla,"k",function(k) {})            # 生产函数求导
f <- function(k) { eval(f.fmla) }                              # y
df <- function(k) { as.vector(attr(df.fmla(k),"gradient")) }   # y'
dcdt <- function(c,k) {                                # 微分方程 dc/dt
  -du(c)/d2u(c)*(df(k)-delta-rho)
}
dkdt <- function(c,k) {                                # 微分方程 dk/dt
  f(k) -c -delta*k
}
obj <- function(x) {                                   # 联立微分方程组
  c.old <- x[1]
  k.old <- x[2]    
  c(c.old+dcdt(c.old,k.old)*dt - c,
    k.old+dkdt(c.old,k.old)*dt - k)
}
kss <- ((rho+delta)/alpha)^(1/(alpha-1))               # 稳态
css <- f(kss) - delta*kss                    

3. 搜索鞍点路径

c.grid <- seq(0.01,2*css,length.out=20)                # 设置取值范围和格点
k.grid <- seq(0.01,2*kss,length.out=20) 
c.stable =vector()
k.stable =vector()
s=1
c.stable[s] <- css;  k.stable[s] <- kss        
dt <- 0.1
# 左侧鞍点路径
c <- css; k <- kss                                     # 从稳态出发
while (k>min(k.grid)) {  
  left <- nleqslv(x=c(c-dt,k-dt),fn=obj)               # 解联立方程组
  c <- left$x[1]
  k <- left$x[2]  
  c.stable[s] <- c
  k.stable[s] <- k
  s <- s+1
}
# 右侧鞍点路径
c <- css; k <- kss 
while (k<max(k.grid)) {  
  right <- nleqslv(x=c(c+dt,k+dt),fn=obj)
  c <- right$x[1]
  k <- right$x[2]
  c.stable[s] <- c
  k.stable[s] <- k 
  s <- s+1  
}

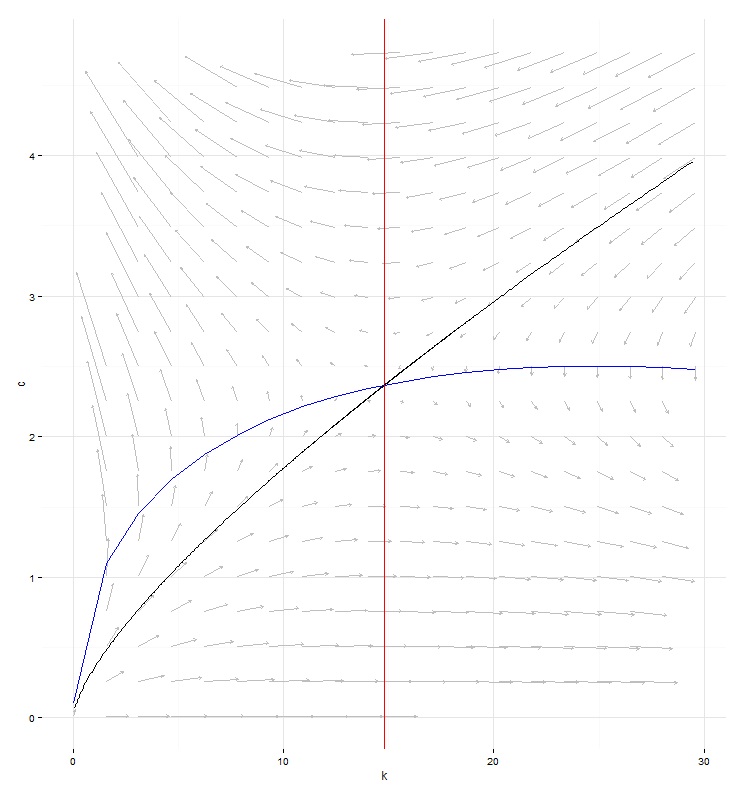
4. 相图

d <- data.frame(c=as.vector(outer(0*k.grid,c.grid,FUN="+")),
                k=as.vector(outer(k.grid,0*c.grid,FUN="+")))
d$dc <- dcdt(d$c,d$k)
d$dk <- dkdt(d$c,d$k)
d$zerodk <- f(d$k)-delta*d$k                            # dk=0的稳态分界线
stable <- data.frame(k=k.stable,c=c.stable)             # 鞍点路径
ggplot(data=d) +
  geom_segment(data=d,aes(x=k,y=c,yend=(c+dc),xend=(k+dk)),
               arrow=arrow(length=unit(0.1,"cm")),colour="gray") +
  geom_line(aes(x=k,y=zerodk),colour="blue") +
  geom_vline(xintercept=kss,colour="red") +             # dc=0的稳态分界线
  geom_line(data=stable,aes(x=k,y=c),colour="black") +
  xlim(min(k.grid),max(k.grid)) +
  ylim(min(c.grid),max(c.grid)) + theme_minimal()