@zhuanxu
2018-01-11T03:51:24.000000Z
字数 4211
阅读 2472
吴恩达 Coursera 第二课记录
吴恩达
划分数据集:train,dev,test
- Train sets 用来训练你的算法模型
- Dev sets 用来验证不同算法的表现情况,从中选择最好的算法模型
- Test sets 用来测试最好算法的实际表现,作为该算法的无偏估计
这3个集合在数量不大,如:100,1000,10000的时候,设置为60%、20%、20%,或者70% 和 30%(无dev);
大数据时代,对于 100 万的样本,往往也只需要 10000 个样本就够了,对于大数据样本,Train/Dev/Test sets 的比例通常可以设置为 98%/1%/1%,或者 99%/0.5%/0.5%。样本数据量越大,相应的 Dev/Test sets 的比例可以设置的越低一些。
上述这么划分数据的一个前提假设是:训练样本和测试样本来自于相同分布。
举个例子,假设你开发一个手机 app,可以让用户上传图片,然后 app 识别出猫的图片。在 app 识别算法中,你的训练样本可能来自网络下载,而你的验证和测试样本可能来自不同用户的上传。从网络下载的图片一般像素较高而且比较正规,而用户上传的图片往往像素不稳定,且图片质量不一。因此,训练样本和验证 / 测试样本可能来自不同的分布。
我们在参加比赛的时候,一般不需要去设置testset,Test sets 的目标主要是进行无偏估计。我们可以通过 Train sets 训练不同的算法模型,然后分别在 Dev sets 上进行验证,根据结果选择最好的算法模型。
Bias/Variance
- high bias。 减少 high bias 的方法通常是增加神经网络的隐藏层个数、神经元个数,训练时间延长,选择其它更复杂的 NN 模型等。
- high variance。减少 high variance 的方法通常是增加训练样本数据,进行正则化 Regularization,选择其他更复杂的 NN 模型等。
传统机器学习算法中,Bias 和 Variance 通常是对立的,减小 Bias 会增加 Variance,减小 Variance 会增加 Bias。而在现在的深度学习中,通过使用更复杂的神经网络和海量的训练样本,一般能够同时有效减小 Bias 和 Variance。
| 问题 | 优化方法 | |
|---|---|---|
| 高偏差 | 增加复杂度 | |
| 高方差 | 正则化,增加数据 |
正则化常用方法
L2正则化
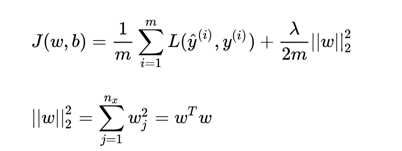
问题:为什么只对 w 进行正则化而不对 b 进行正则化呢?
答:因为w维数高,复杂度远超b。
L1正则化

L1优点:节约存储空间,因为大部分 w 为 0。
缺点:微分求导方面比较复杂。
结论:选择L2 regularization。
L2方法分析
问:为什么L2正则化有效?
答:可以这么理解。
加入正则化后,参数w的更新变为:
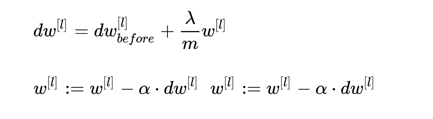
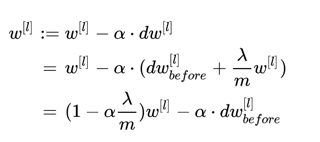
此处显然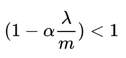 。
。
也就意味着加入L2后,参数w的衰减加快,而我们在神经网络中一般会有一个激活函数,我们以tanh为例:
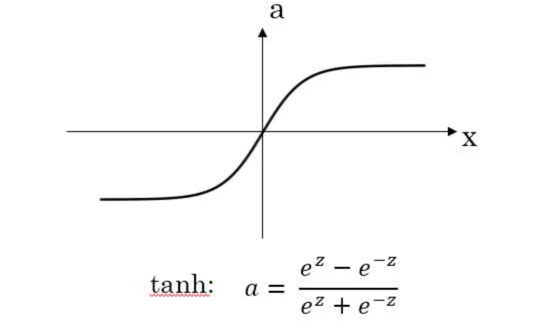
如果w小话,意味着输出小,而tanh在0附近接近于线性,也就意味着网络的非线性整体减小了。
但是如果w过小,意味着某些神经元会不起作用,网络变为:

此时网络的拟合能力变弱,因此我们要选择一个合适的 ,防止w衰减过快。
Dropout
Dropout 有不同的实现方法,下面介绍:
Inverted dropout
keep_prob = 0.8# 保留0.8dl = np.random.rand(al.shape[0],al.shape[1])<keep_probal = np.multiply(al,dl)# scale up 操作al /= keep_prob
对 al 进行 scale up 是为了保证在经过 dropout 后, al 作为下一层神经元的输入值尽量保持不变。
问:dropout为什么起作用?
答:通过随机让某些神经元失效,让结果不依赖于特定的神经元,也就防止了过拟合。
dropout设置原则
- 神经元越多的隐藏层,keep_out 可以设置得小一些,例如 0.5;
- 神经元越少的隐藏层,keep_out 可以设置的大一些,例如 0.8,设置是 1
其他正则方法
- 增加训练样本数量
- data augmentation,例如图片识别问题中,可以对已有的图片进行水平翻转、垂直翻转、任意角度旋转、缩放或扩大等等。
- early stopping
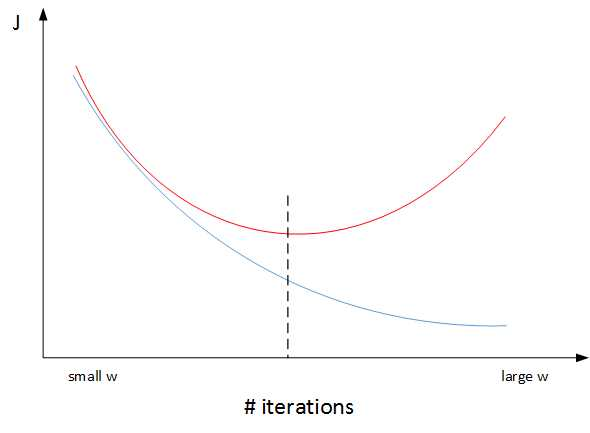
dev set error开始升高时结束训练。
L2 和 early stopping 比较
机器学习训练模型有两个目标:
- 一是优化 cost function,尽量减小 J;
- 二是防止过拟合。
Early stopping 的做法通过减少迭代训练次数来防止过拟合,这样 J 就不会足够小。
L2 regularization,迭代训练足够多,减小 J,而且也能有效防止过拟合。
优选L2 regularization。
输入去均值,归一化

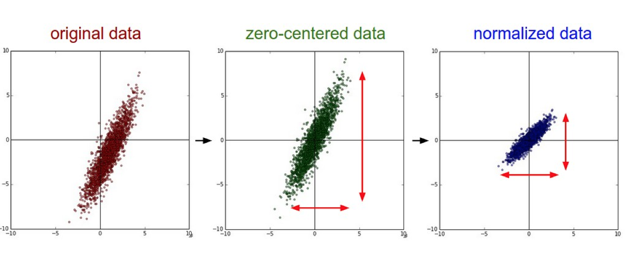
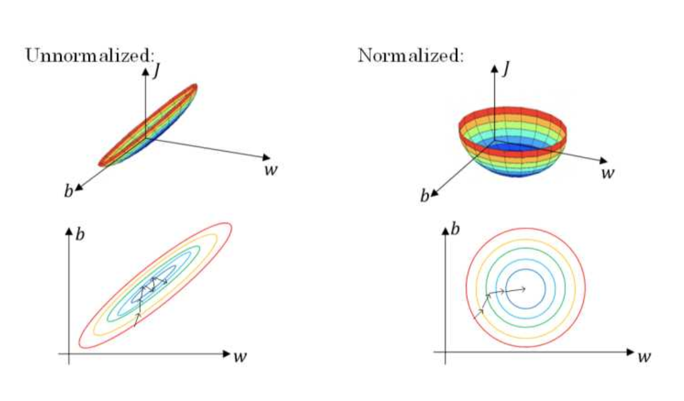
注意:由于训练集进行了标准化处理,那么对于测试集或在实际应用时,应该使用同样的 和 对其进行标准化处理。这样保证了训练集合测试集的标准化操作一致。
权重初始化
深度神经网络模型中,以单个神经元为例,该层( l )的输入个数为 n,其输出为
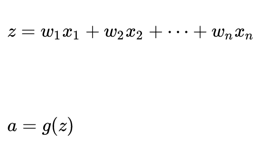
思路:为了让 z 不会过大或者过小,思路是让 w 与 n 有关,且 n 越大,w 应该越小才好。这样能够保证 z 不会过大。一种方法是在初始化 w 时,令其方差为 .
激活函数为tanh时,初始化 w 时,令其方差为 :
w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(1/n[l-1])
激活函数为ReLU,权重 w 的初始化一般令其方差为 :
w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(2/n[l-1])
除此之外,Yoshua Bengio 提出了另外一种初始化 w 的方法,令其方差为 :
w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(2/n[l-1]*n[l])
mini-batch
建议:对于 Mini-Batches Gradient Descent,可以进行多次 epoch 训练。而且,每次 epoch,最好是将总体训练数据重新打乱、重新分成 T 组 mini-batches,这样有利于训练出最佳的神经网络模型。
每个批次大小的建议:
如果总体样本数量 m 不太大时,例如 ,建议直接使用 Batch gradient descent。如果总体样本数量 m 很大时,建议将样本分成许多 mini-batches。推荐常用的 mini-batch size 为 64,128,256,512。这些都是 2 的幂。之所以这样设置的原因是计算机存储数据一般是 2 的幂,这样设置可以提高运算速度。
指数加权平均
公式
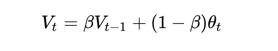
近似有效的的值为:
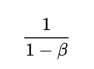
梯度下降方法
动量梯度下降算法

原始的梯度下降算法如上图蓝色折线所示。在梯度下降过程中,梯度下降的振荡较大,尤其对于 W、b 之间数值范围差别较大的情况。此时每一点处的梯度只与当前方向有关,产生类似折线的效果,前进缓慢。而如果对梯度进行指数加权平均,这样使当前梯度不仅与当前方向有关,还与之前的方向有关,这样处理让梯度前进方向更加平滑,减少振荡,能够更快地到达最小值处。
权重 W 和常数项 b 的指数加权平均表达式如下:

整个算法流程:

初始时,令 。一般设置 ,即指数加权平均前 10 天的数据,实际应用效果较好。
RMSprop
更新公式:
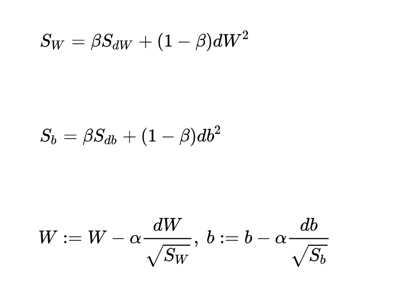
图示:

震荡的是一般的梯度下降,平缓的是 RMSprop。
原理是:哪个方向振荡大,就减小该方向的更新速度,从而减小振荡。
为了防止分母为0,我们一般会修正如下:

Adam
Adam(Adaptive Moment Estimation)算法结合了动量梯度下降算法和 RMSprop 算法。其算法流程为:

所以我们一般会选择 Adam 算法。
学习率的设置
学习率衰减:

其中,deacy_rate 是参数(可调),epoch 是训练完所有样本的次数。随着 epoch 增加,
会不断变小。
整体思路是:随着训练次数的增加,减少学习率。
调优步骤
深度神经网络需要调试的超参数(Hyperparameters)较多,包括:
- :学习因子
- :动量梯度下降因子
- :Adam 算法参数
- #layers:神经网络层数
- #hidden units:各隐藏层神经元个数
- learning rate decay:学习因子下降参数
- mini-batch size:批量训练样本包含的样本个数
我们可以大致根据上面的顺序,挨个调整参数,直至最优。
对于神经网络层数选择的一个经验是:
像CTR预估中,3层神经网络效果优于2层神经网络,但是如果把层数再不断增加(4,5,6层),对最后结果的帮助就没有那么大的跳变了。
而图像和音频处理比较特殊,需要更深的网络,这样子能更准确的提取图像、音频信息。
在具体的超参数选择上,我们通过随机化选择参数的方法:
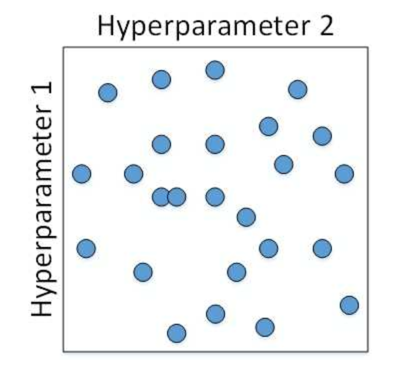
在确定一个范围后,然后再在此基础上缩小区域,重新随机选择参数:
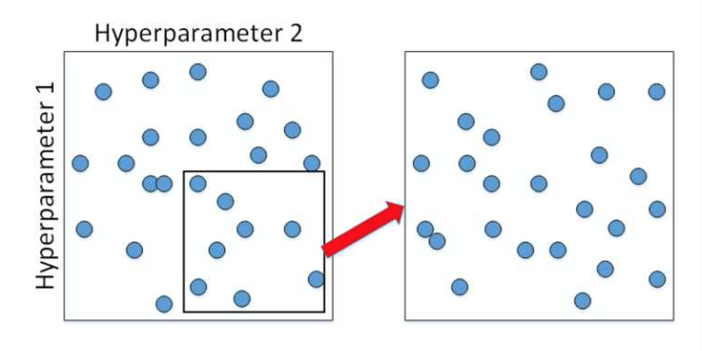
Batch Normalization
对于激活函数的输出在作为下一层输出前,做如下处理:
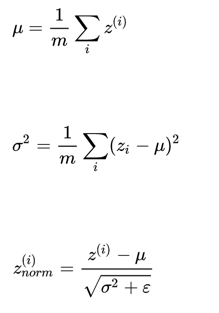
但是从激活函数的角度来说,如果各隐藏层的输入均值在靠近 0 的区域即处于激活函数的线性区域,这样不利于训练好的非线性神经网络,得到的模型效果也不会太好,于是有了下面的修正:

Batch Normalization at test time
如何在测试中使用 Batch Normalization?预测中只有一个样本输入,我们无法求均值和方差,因此我们就要去估计这个测试过程中的均值和方差。
一种估计方法是:使用训练过程中的均值和方差;
另外一种是:指数加权平均。
指数加权平均的做法很简单,对于第 l 层隐藏层,考虑所有 mini-batch 在该隐藏层下的 和 ,然后用指数加权平均的方式来预测得到当前单个样本的 和 。这样就实现了对测试过程单个样本的均值和方差估计。最后,再利用训练过程得到的 和 值计算出各层的 值。
总结
本文是对吴恩达深度学习课程的一个记录。笔记更多的是给自己记录一个List,让以后实际工作中能够按照这个list来做网络的调试工作。
另外推荐知乎专栏红色石头的机器学习之路,里面对吴恩达的视频课可以说是给出了视频的文字稿件,方便我们回顾主要内容,非常感谢红色石头的!
你的鼓励是我继续写下去的动力,期待我们共同进步。

