EM算法的9重境界之前两重

机器学习 EM

最近读了EM算法的九层境界：Hinton和Jordan理解的EM算法，我自己重新找了里面的资料来读的，重新补充了里面自己不懂的地方，先来介绍前两重境界：

1. EM 就是 E + M
2. EM 是一种局部下限构造

第一层境界， EM算法就是E 期望 + M 最大化

拜读了Chuong B Do & Serafim Batzoglou的Tutorial论文“What is the expectation maximization algorithm?“，里面举个例子非常好的说明了EM算法。

假设我们有两枚硬币，我们随机选一枚硬币，然后抛10次，记录下正反面，重复选择5次，总共抛50次，现在估算两枚硬币跑出正面的概率：

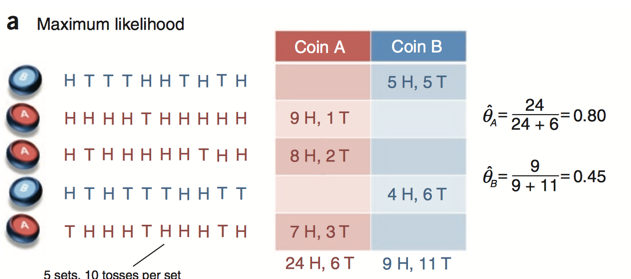
此处每次选择的硬币是已知的，我们可以通过最大似然估计很简单的计算出每枚硬币跑出正面的概率，就是简单的数数即可.

下面稍微提升点难度，我们不告诉你每次选择到的硬币是A还是B
,只告诉你每次抛出的正反面情况，此时相当于我们观察到的数据的是不完整的，多了一个隐藏变量z：每次硬币是A还是B。于是我们的做法是：先假设两枚硬币抛出正面的概率已知，然后根据抛出的正反面次数计算A或者B的概率，再根据最大似然计算出新的两枚硬币抛出正面的概率，下面是是这个过程的图形说明：

再来总结下上图中的步骤
1. 估算$\theta_A=0.6,\theta_B=0.5$
2. E-step:根据正反面情况，计算属于A,B的概率$P(A),P(B)$
3. M-step:数数，根据正反面的个数重新计算$\theta_A,\theta_B$
4. 重复上面过程，直到$\theta_A,\theta_B$收敛

下面是一些数学上的描述：

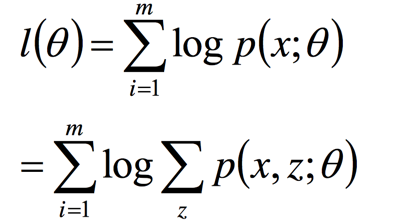
上面这个数学式子的难点在于log内部有个求和符号，导致我们不能方便的求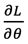，所以我们想办法将求和符号放到log外面，于是就有了下面的式子：

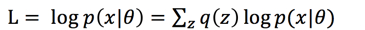
此处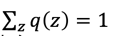，我们接着上面的式子做下面的变换：


针对上面的公式我们有结论：

于是就有了E-step和M-step

先做E-step，当KL散度=0时候，求得p(z|x,theta)=q(z)，即先验等于后验，再做M-step，将求得的p(z|x,theta)带入式子，求新的theta。

第二层境界， EM算法就一种局部下限构造

根据上面的推导，我们可以画图来表示整个过程：

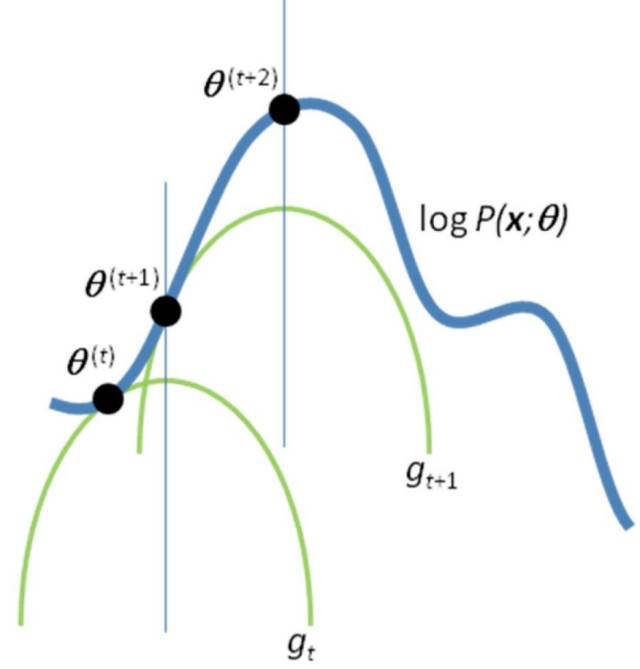
解释下，对于$\theta^{t}$点，是KL散度等于0的点，此时我们只剩下项，是我们的下界，此时我们求下界的最大值$\theta^{t+1}$，此时在$\theta^{t+1}$条件下，我们又求得新的KL散度为0的下界，再重新求下界的极值，不断重复这个过程，我们就能逼近真正的极值点。

本文只是EM算法的九层境界：Hinton和Jordan理解的EM算法中的前两层境界，后续文章将继续修炼剩下的7层境界。