贝叶斯统计：Gibbs sampling 原理到实践

贝叶斯 lda gibbs

---

经过前面两篇文章，我们终于来到了Gibbs samping，为什么我这么兴奋呢？因为我当初看贝叶斯推断就是因为LDA模型，里面用到了Gibbs sampling的方法来解参数问题。
好了下面开始介绍Gibbs 采样。

Gibbs采样

前面一篇文章我介绍了细致平稳条件，即：

$$\pi(x)k(x^*|x) = \pi(x^*)k(x|x^*)$$
Gibbs采样的算法如下：

我们来证明Gibbs采样算法也满足细致平稳条件。

假设x = x 1 , . . . , x D ，当我们采样第k个数据的时候，


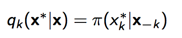
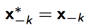
此时我们的接受率为：


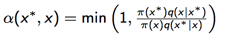
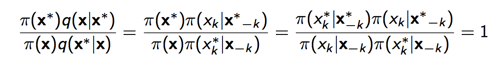
上面公式一个关键的部分是：
$\pi(x^*)=\pi(x_{k}^{*}|x_{-k}^{*})\pi(x_{-k}^{*})$,
$\pi(x)=\pi(x_{k}|x_{-k})\pi(x_{-k})$
带入就可以得到1，即gibbs采样是一定接受的采样。

下面我们照惯例还是来一个例子。

例子

假设有我们有数据x1,x2...xN，其中1-n的数服从一个泊松分布，n+1-N的数服从另一个泊松分布。
而泊松分布的参数$\lambda$服从Gamma分布，我们总结下目前的先验假设：

此时后验概率是：


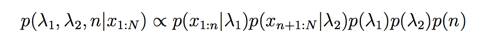
我们下一步开始我们的采样,先计算下logP：

接着来采样$\lambda_{1},\lambda_{2}$


我们此处只取了跟当前采样参数有关的项，因为其他都是一些常数，作用只是将概率分布归一化，不影响采样。
此处$\lambda_{1},\lambda_{2}$都服从Gamma分布。
最后是n:

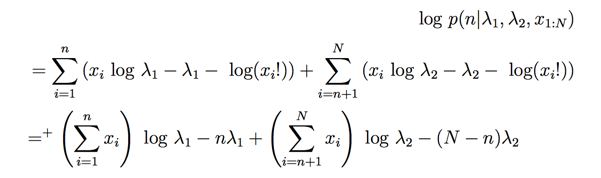
n没有显示的分布信息，但是我们简单将其认为是一个多项分布。
下面是关键Python代码：

完整代码见Gibbs
采样后输出如下图：

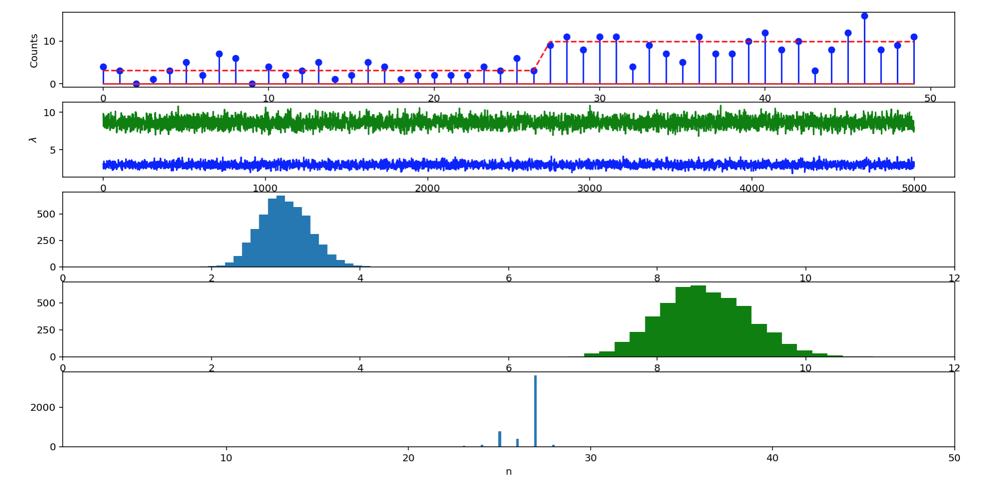
LDA

下面我们来最激动人心的LDA模型，看怎么用Gibbs 采样来解。

先看LDA的模型：

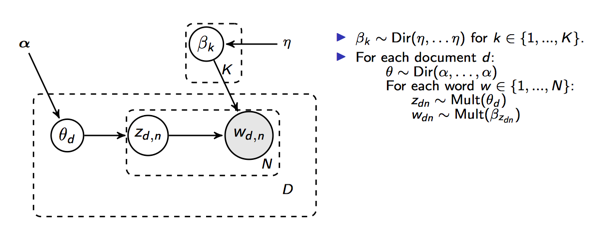
整个过程可以描述为

1. 对于文档d，从$Dir(\alpha)$分布中采样出$\theta_d$，即文档d的主题分布
2. 对于文档的每个词$w_{d,n}$从多项分布$\theta_d$中采样出主题k，即$z_{d,n}=k$
3. 对于主题k，从$Dir(\eta)$中采样出$\beta_k$，即主题k的词分布
4. 对于每个词$w_{d,n}$，从主题分布$\beta_{z_{d,n}}$中采样出具体的单词t

上面整个模型中，模型参数有：

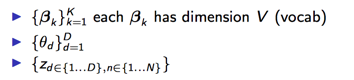
为了做Gibbs采样，我们先看这几个参数的联合分布。

$$p(z_m,\theta_m,\Phi | w_m) \propto p(w_m|z_m,\Phi) p(z_m|\theta_m)p(\theta_m|\alpha)p(\Phi|\eta )$$
$$= \prod_{n=1}^{N_m}p(w_{m,n}|z_{m,n},\Phi)p(z_{m,n}|\theta_m)p(\theta_m|\alpha)p(\Phi|\eta )$$

上面公式中$p(w_m|z_m,\Phi),p(z_m|\theta_m)$是多项分布，而$p(\theta_m|\alpha),p(\Phi|\eta )$是Dir分布，我们知道Dir分布和多项分布是共轭分布，因此后验分布比较容易写出来。

下面我们开始计算每个参数的概率，主要是计算下面3个概率：



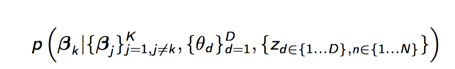
先来计算第一个主题的概率分布：

$$p(\theta_m|z_m,\Phi,w_m) \propto \prod_{n=1}^{N_m}p(z_{m,n}|\theta_m)p(\theta_m|\alpha)=Dir(\theta_m|\alpha+n_m)$$
其中$n_m=(n_{1}^{m},n_2^m,...,n_K^m)$表示第m篇文档中，属于每个主题的词个数。
接着计算每个主题的词分布
$$p(\beta_k|\beta_{-k},w_m,z_m,\theta_m,) \propto \prod_{n=1}^{N_m}p(w_{m,n}|z_{m,n}=k,\beta_k)p(\beta_k|\eta)=Dir(\beta_k|\eta+n_k)$$
其中$n_k=(n_{1}^{k},n_2^k,...,n_V^k)$第m篇文档中属于k个主题的，每个单词的数量，共(1-V)个单词。
最后来估算每个词的主题。
$$\begin{align} p(z_{m,j}=k) &\propto p(w_{m,j}|z_{m,j}=k,\Phi)p(z_{m,j}=k|\theta_m) \\ &= p(w_{m,j}|\beta_k)p(z_{m,j}=k|\theta_m) \\ &= \beta_{k,w_{m,j}} \theta_{mk} \end{align}$$

我们可以看到$p(z_{m,j})$是一个多项分布，每一项的概率都是$\beta_{k,w_{m,j}} \theta_{mk}$，而他们本身也是需要从Dir分布中采样出来的，一个自然的想法就是我们可以用估计值来代替$\widehat{\beta}_{k,w_{m,j}}, \widehat{\theta}_{mk}$，根据Dir分布我们能够很方便的计算出概率来。
此处需要的数学基础可以看主题模型：LDA 数学基础。

里面一个点是Dir分布和其数学期望

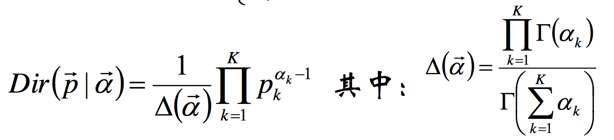
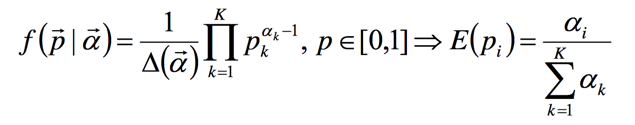
我们上面在Gibbs采样中计算分别采样$\theta,\beta$都可以用Dir分布的的期望来作为新的参数值。

编码

介绍完数学基础后，我么就能来看如何实现了，下面是一个伪代码。

for m in range(D): // 遍历每篇文档
    for n in range(W[m]): // 遍历每篇文档的单词
        w = W[m][n] // 单词 w
        k = z[m][n] // 主题 k
        nd[m,k] -= 1 // 第m篇文档第k个主题的词数目
        ndsum[m, 0] -= 1 // 第m篇文档总的主题词数目sum(nd[m])
        nw[k, w] -= 1 // 第k个topic中产生w的数目
        nwsum[k, 0] -= 1 // 第k个topic总共产生的w数目
        # 计算theta值，Dir分布的期望
        theta_p = (nd[m] + alpha) / (ndsum[m, 0] + sum_alpha)
        # 计算beta的期望值
        beta_p = (nw[:, w] + beta[w]) / (nwsum[:, 0] + sum_beta)
        # multi_p为多项式分布的参数
        multi_p = theta_p * beta_p
        # 多项式采样新的k
        k = mul_sample(multi_p)
        nd[m,k] += 1 // 第m篇文档第k个主题的词数目
        ndsum[m, 0] += 1 // 第m篇文档总的主题词数目sum(nd[m])
        nw[k, w] += 1 // 第k个topic中产生w的数目
        nwsum[k, 0] += 1 // 第k个topic总共产生的w数目
        z[m][n] = k// 更新主题

完整的代码可以见玩点高级的 -- 带你入门 Topic 模型 LDA（小改进 + 附源码）

pymc3 实现

下面我们再来用pymc3来实现下。

可以说pymc3写出来的代码真是简洁。but。就是太慢了，完整的代码可以看gibbs-lda。

总结

本文介绍了mh算法的特例Gibbs采样，并且给出了证明为什么Gibbs采样work，最后我们用Gibbs采样来解决了LDA的参数估计问题。

你的鼓励是我继续写下去的动力，期待我们共同进步。