动态规划

algorithm

认知

认识事物的方法：概念、判断、推理，而推理又分为归纳、演绎。

数学归纳法

最简单和常见的数学归纳法是证明当n等于任意一个自然数时某命题成立。证明分下面两步：

1. 证明当n = 1 时命题成立。
2. 证明如果在n = m时命题成立，那么可以推导出在n = m+1 时命题也成立。（m代表任意自然数）

整个过程就像多米诺骨牌，只要前一个倒下，那么与其相邻的下一张骨牌也会倒。

第二数学归纳法

第二数学归纳法原理是设有一个与正整数 n 有关的命题，如果：
（1）当 n=1 时，命题成立；
（2）假设当 n≤k（k∈N）时，命题成立，由此可推得当 n=k+1 时，命题也成立。
那么根据①②可得，命题对于一切正整数 n 来说都成立。

上面两个的区别就在于对信息的使用上：

• 基本归纳法：对于n ，只需考察前一个状态 n-1 即可完成整个推理过程，我们将这一模型称为马尔科夫模型；
• 高阶归纳法：相应的，对于 n, 考察前n-1个状态集{1,2...n-1} 才可完成整个推理过程，往往称之为高阶马尔科夫模型；
• 在计算机算法中，高阶马尔科夫模型的推理，叫做“动态规划”， 而马尔科夫模型的推理，对应“贪心法”。
  
  

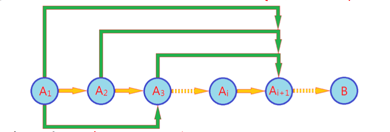
套路:3+1

1. 计算过程可视化
   当面对问题无头绪的时候，我们尝试着将自己的思路画出来，能有助于我们理清思路。
2. 子问题拆解
   计算机思维中一个很重要的就是通过模块化，将复杂问题拆解为一系列简单的问题。
3. 打破假设
   这是寻找到新解法的关键，我们需要突破假设，才能找到另一片天地。

还有最后一个原则就是类比，我们需要不断去总结现有的知识，然后将遇到的新东西都建立到我们现有的知识树上。

下面是一些动态规划的具体题目。

股票最大收益

问题描述：
给定数组A[1,2...N]，其中A[i]表示某股票第i天的价格，我们同时最多持有一股，如果只能进行一次买卖，如何利润最大化？ 例如股票的变化是：1, 4, 9, 2, 7, 3
最好的方案是：1买9卖，获利8，如果一路下跌，则最好的方法是不进行交易。

我们第一步先讲整个过程可视化。

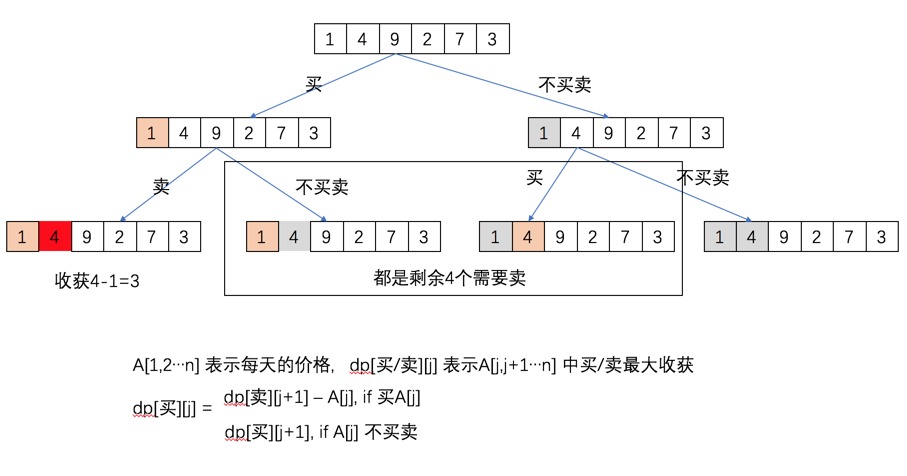
通过画图我们就知道了过程了，下面看代码：

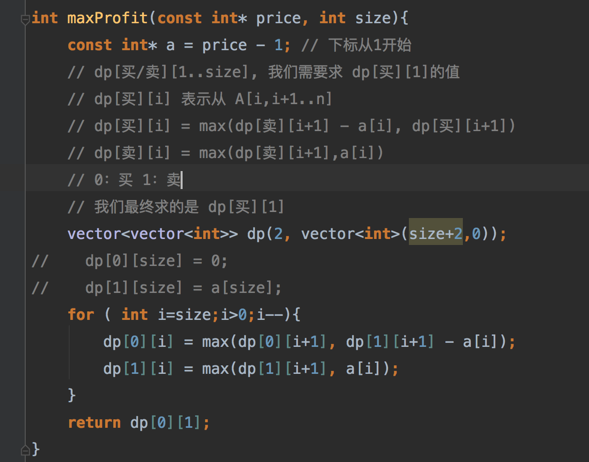
下面我们加大难度，能够进行k次交易，规定买卖不能嵌套，即：买入后，要先卖出才可再买。
如：A=[7,1,5,3,6,4]，K=3，则在1,3处买入， 5,6处卖出，最大收益为7。

我们还是先来画图:

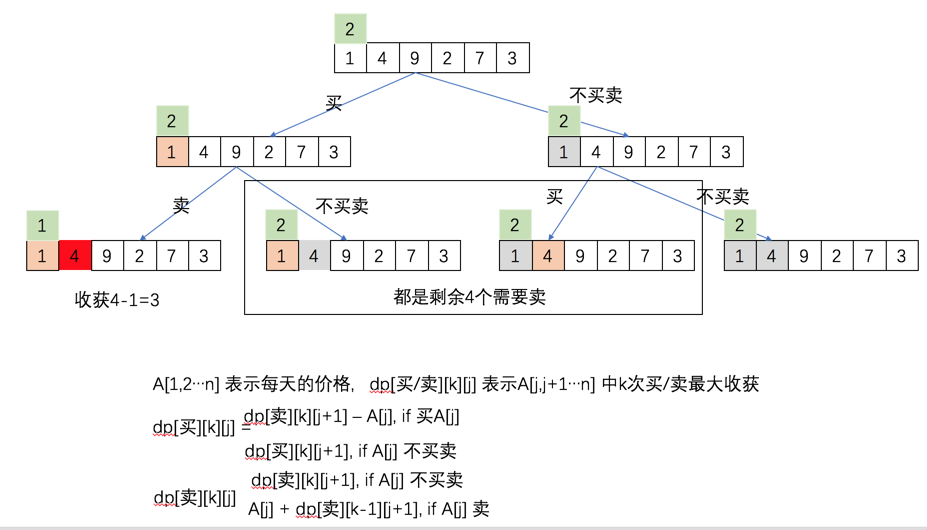
从图中我们就有了下面的代码：

总结

本文复习了下动态规划，并且举了个例子来说如何解决动态规划问题，记住套路：3+1。

你的鼓励是我继续写下去的动力，期待我们共同进步。