回归分析篇

多元线性回归

前一篇讲了一元线性回归，但是实际应用中多半都是要考察多个因素对某个因素的影响，这就需要跨越到多元回归分析了

本篇先介绍多元线性回归分析的一般理论，然后以一个完整的小例子来应用这些理论

多元线性回归模型

设随机变量 $y$ 与一般变量 $x_1,x_2,\cdots,x_p$ 的线性回归模型为

$$y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p + \epsilon$$
其中，$\beta_0,\beta_1,\cdots,\beta_p$ 是 $p+1$ 个未知参数，$\beta_0$ 称为回归常数，$\beta_1,\cdots,\beta_p$ 称为回归系数。$y$ 称为被解释变量(因变量)，而 $x_1,x_2,\cdots,x_p$ 是 $p$ 个可以精确测量并可控制的一般变量，称为解释变量(自变量)。我们称上述式子为多元线性回归模型。$\epsilon$是随机误差，与一元线性回归一样，对随机误差项我们常假定 $$\begin{cases} E(\epsilon) = 0 \\ var(\epsilon) = \sigma^2 \end{cases}$$ 称 $$E(y) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p$$ 为理论回归方程

对一个实际的问题，我们获得 $n$ 组观察数据 $(x_{i1},x_{i2},\cdots,x_{ip};y_i),\ \ i = 1,2,\cdots,n$ 则线性回归模型可表示为

$$\begin{cases} y_1 = \beta_0 + \beta_1 x_{11} + \beta_2 x_{12} + \cdots + \beta_p x_{1p} + \epsilon_1 \\ y_2 = \beta_0 + \beta_1 x_{21} + \beta_2 x_{22} + \cdots + \beta_p x_{2p} + \epsilon_2 \\ \cdots \cdots \cdots \\ y_n = \beta_0 + \beta_1 x_{n1} + \beta_2 x_{n2} + \cdots + \beta_p x_{np} + \epsilon_n \end{cases}$$
写成矩阵形式为
$$\boldsymbol{y} = \boldsymbol{X} \boldsymbol{\beta} + \boldsymbol{\epsilon}$$
其中，
$$\boldsymbol{y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix} \\ \boldsymbol{X} = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1p} \\ 1 & x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \vdots & & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{np} \end{bmatrix} \\ \boldsymbol{\beta} = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_p \end{bmatrix} \\ \boldsymbol{\epsilon} = \begin{bmatrix} \epsilon_0 \\ \epsilon_1 \\ \vdots \\ \epsilon_p \end{bmatrix}$$

矩阵 $X$ 是一 $n\times(p+1)$ 矩阵，称 $X$ 为回归设计矩阵或资料矩阵。在实验设计中，$X$ 的元素是预先设定并可以控制的，人的主观因素可作用于其中，因而称 $X$ 为设计矩阵。

多元线性回归模型的基本假定

为了方便地进行模型的参数估计，对方程由如下一些基本假定:

1. 解释变量 $x_1,x_2,\cdots,x_p$ 是确定性变量，不是随机变量，且要求 $rank(X) = p+1 < n$。这里的 $rank(X) = p+1 < n$，表明设计矩阵 $X$ 中的自变量列之间不相关，样本容量的个数应大于解释变量的个数，$X$ 是一满秩矩阵.

2. 随机误差项具有0均值和等方差，即

   $$\begin{cases} E(\epsilon_i) = 0,\ \ i=1,2,\cdots,n \\ cov(\epsilon_i,\epsilon_j) = \begin{cases} \sigma^2,i=j \\ 0,\ i \neq j \end{cases} \ \ (i,j = 1,2,\cdots,n) \end{cases}$$
   这个假定常称为高斯-马尔科夫条件。$E(\epsilon_i) = 0$，即假设观察值没有系统误差，随机误差 $\epsilon_i$ 的平均值为零。随机误差项 $\epsilon_i$ 的协方差为零表明随机误差项在不同的样本点之间是不相关的(在正态假定下即为独立的)，不存在序列相关，并且有相同的精度。

3. 正态分布的假定条件为

   $$\begin{cases} \epsilon_i \approx N(0,\sigma^2), \ \ i=1,2,\cdots,n \\ \epsilon_1,\epsilon_2,\cdots,\epsilon_n \ \ 相互独立 \end{cases}$$
   对于多元线性回归的矩阵形式可表示为 $$\boldsymbol{\epsilon} \approx N(\boldsymbol{0}, \sigma^2\boldsymbol{I}_n)$$

有上述假定和多元正态分布的性质可知，随机向量 $y$ 遵从 $n$ 维正态分布，回归模型的期望向量

$$E(y) = \boldsymbol{X}\boldsymbol{\beta} \\ var(y) = \sigma^2\boldsymbol{I}_n$$
因此， $$y \approx N(\boldsymbol{X}\boldsymbol{\beta}, \sigma^2\boldsymbol{I}_n)$$

---

多元线性方程组的普通最小二乘法

多元线性回归方程未知参数 $\beta_0,\beta_1,\cdots,\beta_p$ 的估计与一元线性回归方程的参数估计原理一样，任然可以采用最小二乘法估计。

与一元线性回归方程的最小二乘法推导一致，寻找 $\hat{\beta_0},\hat{\beta_1},\hat{\beta_2},\cdots,\hat{\beta_p}$ 满足

$$Q(\hat{\beta_0},\hat{\beta_1},\hat{\beta_2},\cdots,\hat{\beta_p}) = \sum_{i=1}^n{(y_i - \hat{\beta_0} - \hat{\beta_1} x_{i1} - \hat{\beta_2} x_{i2} - \cdots - \hat{\beta_p} x_{ip})^2} \\ = \min_{\beta_0,\beta_1,\beta_2,...,\beta_p}{\sum_{i=1}^n{(y_i - \beta_0 - \beta_1 x_{i1} - \beta_2 x_{i2} - ... - \beta_p x_{ip})^2}}$$
求出的 $\hat{\beta_0},\hat{\beta_1},\hat{\beta_2},\cdots,\hat{\beta_p}$ 就称为回归参数 $\beta_0,\beta_1,\cdots,\beta_p$ 的最小二乘估计

这是个求极值的问题，于是求偏导得

$$\begin{cases} \left.\frac{\partial Q}{\partial \beta_0} \right|_{\beta_0 = \hat{\beta_0}} = -2 \sum_{i=1}^n{(y_i - \hat{\beta_0} - \hat{\beta_1} x_{i1} - \hat{\beta_2} x_{i2} - \cdots - \hat{\beta_p} x_{ip})} = 0 \\ \left.\frac{\partial Q}{\partial \beta_1} \right|_{\beta_1 = \hat{\beta_1}} = -2 \sum_{i=1}^n{(y_i - \hat{\beta_0} - \hat{\beta_1} x_{i1} - \hat{\beta_2} x_{i2} - \cdots - \hat{\beta_p} x_{ip})x_{i1}} = 0 \\ \left.\frac{\partial Q}{\partial \beta_2} \right|_{\beta_2 = \hat{\beta_2}} = -2 \sum_{i=1}^n{(y_i - \hat{\beta_0} - \hat{\beta_1} x_{i1} - \hat{\beta_2} x_{i2} - \cdots - \hat{\beta_p} x_{ip})x_{i2}} = 0 \\ \\ \\ \cdots \cdots \\ \left.\frac{\partial Q}{\partial \beta_p} \right|_{\beta_p = \hat{\beta_p}} = -2 \sum_{i=1}^n{(y_i - \hat{\beta_0} - \hat{\beta_1} x_{i1} - \hat{\beta_2} x_{i2} - \cdots - \hat{\beta_p} x_{ip})x_{ip}} = 0 \end{cases}$$
以上方程组经整理后，用矩阵的形式表示为:
$$\boldsymbol{X}'(\boldsymbol{y} - \boldsymbol{X}'\boldsymbol{\hat{\beta}}) = \boldsymbol{0}$$ 移项得:
$$\boldsymbol{X}'\boldsymbol{X}\boldsymbol{\hat{\beta}} = \boldsymbol{X}'\boldsymbol{y}$$ 当 $(\boldsymbol{X}'\boldsymbol{X})^{-1}$存在时，即得到回归参数的最小二乘估计为 $$\boldsymbol{\hat{\beta}} = (\boldsymbol{X}'\boldsymbol{X})^{-1}\boldsymbol{X}'\boldsymbol{y}$$ 称$\hat{y} = \hat{\beta_0} + \hat{\beta_1} x_1 + \hat{\beta_2} x_2 + ... + \hat{\beta_p} x_p$为经验回归方程。

---

回归值与残差

在求出回归参数的最小二乘估计后，就可以用经验回归方程求出因变量的回归值与残差:

$$\hat{y_i} = \hat{\beta_0} + \hat{\beta_1} x_{i1} + \hat{\beta_2} x_{i2} + ... + \hat{\beta_p} x_{ip}$$ 为观测值 $y_i(i = 1,2,...,n)$ 的回归拟合值，简称回归值或拟合值;
$$\hat{y} = \boldsymbol{X}\boldsymbol{\hat{\beta}} = \boldsymbol{X}(\boldsymbol{X}'\boldsymbol{X})^{-1}\boldsymbol{X}'\boldsymbol{y}$$ 可看到，矩阵$\boldsymbol{X}(\boldsymbol{X}'\boldsymbol{X})^{-1}\boldsymbol{X}'$的作用是把因变量向量 $\boldsymbol{y}$ 变为拟合值向量 $\boldsymbol{\hat{y}}$ ，从形式上看是给 $\boldsymbol{y}$ 戴上一顶帽子"$\hat{}$"，因而形象的称矩阵 $\boldsymbol{X}(\boldsymbol{X}'\boldsymbol{X})^{-1}\boldsymbol{X}'$ 为帽子矩阵，记为 $\boldsymbol{H}$，于是 $\boldsymbol{\hat{y}} = \boldsymbol{H}\boldsymbol{y}$ 。帽子矩阵 $\boldsymbol{H} = \boldsymbol{X}(\boldsymbol{X}'\boldsymbol{X})^{-1}\boldsymbol{X}'$ 的主对角元素记为 $h_{ii}$ ，可以证明，帽子矩阵 $\boldsymbol{H}$ 的迹为 $$tr(\boldsymbol{H}) = \sum_{i=1}^2{h_{ii}} = p + 1$$

称

$$e_i = y_i - \hat{y_i}$$ 为 $y_i(i=1,2,...,n)$的残差，称$\boldsymbol{e} = (e_1,e_2,...,e_n) = \boldsymbol{y} - \boldsymbol{\hat{y}}$ 为回归残差向量。将 $\boldsymbol{\hat{y}} = \boldsymbol{H}\boldsymbol{y}$ 代入得 $\boldsymbol{e} = \boldsymbol{y} - \boldsymbol{h}\boldsymbol{y} = (\boldsymbol{I} - \boldsymbol{H})\boldsymbol{y}$

记$cov(\boldsymbol{e},\boldsymbol{e}) = (cov(e_i,e_j))_{n \times n}$ 为残差向量 $\boldsymbol{e}$ 的协方差阵，或称方差阵，记为 $D(\boldsymbol{e})$，因而

$$D(\boldsymbol{e}) = cov(\boldsymbol{e},\boldsymbol{e}) \\ = cov((\boldsymbol{I} - \boldsymbol{H})\boldsymbol{y},(\boldsymbol{I} - \boldsymbol{H})\boldsymbol{y}) \\ = (\boldsymbol{I} - \boldsymbol{H})cov(\boldsymbol{y},\boldsymbol{y})(\boldsymbol{I} - \boldsymbol{H})' \\ = \sigma^2(\boldsymbol{I} - \boldsymbol{H})I_n(\boldsymbol{I} - \boldsymbol{H})' \\ = \sigma^2(\boldsymbol{I} - \boldsymbol{H})$$
于是有 $D(e_i) = (1 - h_{ii})\sigma^2, \ \ i = 1,2,...,n$

---

回归方程的显著性检验

在实际问题的研究中，我们事先并不能断定随机变量$y$与变量$x_1,x_2,\cdots,x_p$之间确实有线性关系，我们对$y$与变量$x_1,x_2,\cdots,x_p$做多元线性回归拟合，只是根据一些定性分析所作的假设。

因此，当求出线性回归方程后，还需要对回归方程进行显著性检验。

与一元回归分析类似，多元回归分析这里介绍两种统计检验方法，回归方程显著性的 $F$检验，以及回归系数显著性的 $t$检验；同时介绍衡量回归拟合程度的拟合优度检验

$F$检验

与一元线性回归的 $F$检验类似的提出原假设，由于有多元，所以原假设为

$$H_0: \beta_1 = \beta_2 = \cdots = \beta_p = 0$$ 如果$H_0$被接受，则表明随机变量 $y$与$x_1,x_2,\cdots,x_p$之间的关系由线性回归模型表示不合适。

为了建立对 $H_0$进行检验的 $F$统计量，任然利用总离差平方和分解式，即

$$\sum_{i=1}^n{(y_i - \overline{y})^2} = \sum_{i=1}^n{(\hat{y}_i - \overline{y})^2} + \sum_{i=1}^n{(y_i - \hat{y}_i)^2}$$ 简写为 $$SST = SSR + SSE$$

该总离差平方和分解式的推导过程可参考一元线性回归中的过程

构造 $F$检验统计量如下:

$$F = \frac{SSR/p}{SSE/(n-p-1)}$$ 在正态假设下，当原假设成立时，$F$服从自由度为$(p,n-p-1)$的$F$分布。

对于给定的数据，$i = 1,2,\cdots,n$，计算出$SSR$和$SSE$，进而得到$F$的值，其计算过程一般列在方差分析表中，再由给定的显著性水平 $\alpha$，查 $F$分布表，得临界值 $F_\alpha(p,n-p-1)$；

其中方差分析表(ANOVA)如下所示:

方差来源	自由度	平方和	均方	F值	P值
回归	$p$	$SSR$	$\frac{SSR}{p}$	$\frac{SSR/p}{SSE/(n-p-1)}$	$P(F>F值) = P值$
残差	$n-p-1$	$SSE$	$\frac{SSE}{n-p-1}$
总和	$n-1$	$SST$

当 $F>F_\alpha(p,n-p-1)$时，拒绝原假设 $H_0$，认为在显著性水平 $\alpha$下，$y$对$x_1,x_2,\cdots,x_p$有显著的线性关系，也就是说回归方程显著；反之，当 $F \leq F_\alpha(p,n-p-1)$时，则认为回归方程不显著。

与一元线性回归一样，也可以根据 $P$值作检验。当 $P值 < \alpha$时，拒绝原假设；当 $P值 \geq \alpha$时，接受原假设。

当回归方程显著时，说明用线性方程来拟合是有效的；当回归方程不显著时，说明自变量与因变量不满足线性关系，这时就需要考虑其他非线性关系，或者对自变量或因变量做变换后再考虑线性关系

---

回归系数的显著性检验

在多元线性回归中，回归方程显著并不意味着每个自变量对 $y$的影响都显著，因此我们总想从回归方程中剔除那些次要的、可有可无的变量，重新建立更为简单的回归方程。所以我们需要对每个自变量进行显著性检验

这里我们使用的是 $t$检验，在一元线性回归分析中，由于只有一个自变量，所以对该自变量进行回归系数的显著性检验也相当于是对回归方程进行显著性检验；但是在多元线性回归分析中，对回归系数的显著性检验与回归方程的显著性检验就不一样了

类似的，检验变量 $x_j$是否显著，等价于检验假设

$$H_{0j} : \beta_j = 0, \ \ \ \ j = 1,2,\cdots,p$$ 如果接受原假设 $H_{0j}$，则 $x_j$不显著；如果拒绝原假设 $H_{0j}$，则 $x_j$显著.

由于

$$\boldsymbol{\hat{\beta}} \approx N(\boldsymbol{\beta},\sigma^2(\boldsymbol{X}'\boldsymbol{X})^{-1})$$ 记 $$(\boldsymbol{X}'\boldsymbol{X})^{-1} = (c_{ij}) \ \ \ \ i,j=0,1,2,\cdots,p$$ 于是有 $$E(\hat{\beta}_j) = \beta_j \\ var(\hat{\beta}_j) = c_{jj}\sigma^2 \\ \hat{\beta}_j \approx N(\beta_j, c_{jj}\sigma^2), j = 0,1,2,\cdots,p$$
据此可以构造 $t$统计量 $$t_j = \frac{\hat{\beta}_j}{\sqrt{c_{jj}}\hat{\sigma}}$$ 其中 $$\hat{\sigma} = \sqrt{\frac{1}{n-p-1} \sum_{i=1}^n{e_i^2}} = \sqrt{\frac{1}{n-p-1} \sum_{i=1}^n{(y_i - \hat{y}_i)^2}}$$ 是回归标准差.

当原假设 $H_{0j} : \beta_j = 0$ 成立时，上式构造的 $t_j$统计量服从自由度为 $n-p-1$的 $t$分布。

给定显著性水平 $\alpha$，查出双侧检验的临界值 $t_{\alpha/2}$。当 $|t_j| \geq t_{\alpha/2}$时拒绝原假设，认为 $\beta_j$显著不为零，自变量 $x_j$对因变量 $y$的线性效果显著；当 $|t_j| \leq t_{\alpha/2}$ 时接受原假设，认为 $\beta_j$为零，自变量 $x_i$对因变量 $y$的线性效果不显著。

若发现有自变量 $x_j$不显著，则需要考虑剔除掉这些不显著的自变量，可一次只剔除一个变量，先剔除其中 $|t|$值最小的(或$P$值最大的)一个变量，然后再对求得的新的回归方程进行检验，有不显著的变量再剔除，直到保留的变量都对 $y$有显著影响为止

关于如何处理不显著的自变量，在后面讲逐步回归时会详细讲解

---

回归系数的置信区间

当我们有了参数向量 $\boldsymbol{\beta}$的估计量 $\boldsymbol{\hat{\beta}}$时，这两者的接近程度如何呢？这就需要构造 $\beta_j$的一个区间，以 $\hat{\beta}_j$为中心的区间，该区间以一定的概率包含 $\beta_j$

我们知道

$$t_j = \frac{\hat{\beta}_j - \beta_j}{\sqrt{c_{jj}}\hat{\sigma}} \approx t(n-p-1)$$ 仿照一元线性回归系数区间估计的推导过程，可得 $\beta_j$的置信度为 $1-\alpha$的置信区间为 $$(\hat{\beta}_j - t_{\alpha/2} \sqrt{c_{jj}} \hat{\sigma},\ \ \hat{\beta}_j + t_{\alpha/2} \sqrt{c_{jj}} \hat{\sigma})$$

---

拟合优度

拟合优度用于检验回归方程对样本观测值的拟合程度。

在一元线性回归中，定义了样本决定系数 $r^2 = SSR/SST$，在多元线性回归中，同样可以定义样本决定系数为

$$R^2 = \frac{SSR}{SST} = 1 - \frac{SSE}{SST}$$ 样本决定系数 $R^2$的取值在$[0,1]$区间内，$R^2$越接近1，表示回归拟合的效果越好；$R^2$越接近0，表示回归拟合的效果越差。

与 $F$检验相比，$R^2$可以更清楚直观地反映回归拟合的效果，但是并不能作为严格的显著性检验.

称

$$R = \sqrt{R^2} = \sqrt{\frac{SSR}{SST}}$$ 为 $y$关于$x_1,x_2,\cdots,x_p$的样本复相关系数。在两个变量的简单相关系数中，相关系数有正负之分，而复相关系数表示的是因变量 $y$与全体自变量之间的线性关系，它的符号不能由某一个自变量的回归系数的符号决定，因而复相关系数都取正号

实际应用中，人们用复相关系数 $R$来表示回归方程对原有数据拟合程度的好坏，它衡量作为一个整体的 $x_1,x_2,\cdots,x_p$与 $y$的线性关系的大小

---

中心化和标准化

在多元线性回归分析中，因为涉及到多个自变量，自变量的单位往往不同，给利用回归方程进行结构分析带来了一定困难；再因为多元回归涉及的数据量很大，就可能由于舍入误差而使计算结果不理想。因此，对原始数据进行一些处理，尽量避免大的误差是有意义的.

产生舍入误差有两个主要原因:

• 一是回归分析计算中数据量级有很大差异；
• 二是设计矩阵 $\boldsymbol{X}$的列向量近似线性相关时，$\boldsymbol{X}'\boldsymbol{X}$为病态矩阵，其逆矩阵 $(\boldsymbol{X}'\boldsymbol{X})^{-1}$就会产生较大的误差.

中心化

多元线性回归模型的一般形式为

$$y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p + \epsilon$$ 其经验回归方程为 $$\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x_1 + \hat{\beta}_2 x_2 + \cdots + \hat{\beta}_p$$ 此经验回归方程经过样本中心 $(\overline{x}_1,\overline{x}_2,\cdots,\overline{x}_p;\overline{y})$，将坐标原点移至样本中心，即做坐标变换 $$x'_{ij} = x_{ij} - x_j \\ y'_i = y_i - \overline{y}$$ 其中$, \ \ i = 1,2,,\cdots,n;\ \ j = 1,2,\cdots,p$
上述经验方程式即转变为 $$\hat{y}' = \hat{\beta}_1 x'_1 + \hat{\beta}_2 x'_2 + \cdots + \hat{\beta}_p x'_p$$ 即为中心化经验回归方程，常数项为0，而回归系数保持不变。

其中 $\hat{\beta}_0 = \hat{y} - \hat{\beta}_1 \overline{x}_1 - \hat{\beta}_2 \overline{2} - \cdots - \hat{\beta}_p \overline{x}_p$可求出常数项估计值 $\hat{\beta}_0$

中心化就是将经验回归方程作了平移变换，将样本中心移到了坐标原点

---

标准化

在中心化的基础上，为了消除量纲不同和数量级的差异所带来的影响，就需要对样本数据作标准化处理，然后用最小二乘法估计未知参数，求得标准化回归系数

样本数据的标准化公式为

$$x_{ij}^* = \frac{x_{ij} - \overline{x}_j}{\sqrt{L_{jj}}} \\ y_i^* = \frac{y_i - \overline{y}}{\sqrt{L_{yy}}}$$ 其中 $i = 1,2,\cdots,n; \ \ j = 1,2,\cdots,p$
而 $$L_{jj} = \sum_{i=1}^n{(x_{ij}-\overline{x}_j)^2}$$ 是自变量 $x_j(j = 1,2,\cdots,p)$的离差平方和。

---

用最小二乘法求出标准化的样本数据 $(x_{i1}^*,x_{i2}^*,\cdots,x_{ip}^*;y_i^*)$的经验回归方程，记为

$$\hat{y}^* = \hat{\beta}_1^* x_1^* + \hat{\beta}_2^* x_2^* + \cdots + \hat{\beta}_p^* x_p^*$$ 其中，$\hat{\beta}_1^*,\hat{\beta}_2^*,\cdots,\hat{\beta}_p^*$为 $y$对自变量 $x_1,x_2,\cdots,x_p$的标准化回归系数。

标准化包括了中心化，因而标准化的回归常数为0；容易验证，标准化回归系数与普通最小二乘回归系数之间存在关系式

$$\hat{\beta}_j^* = \frac{\sqrt{L_{jj}}}{\sqrt{L_{yy}}} \hat{\beta}_j , \ \ j = 1,2,\cdots,p$$

标准化回归系数是比较自变量对 $y$影响程度相对重要性的一种较为理想的方法，但是我们对回归系数的解释任需谨慎，这是因为当自变量相关时会影响标准化回归系数的大小.

---

相关阵

复相关系数 $R$反映了 $y$与一组自变量的相关性，是整体和共性指标，简单相关系数反映的是两个变量间的相关性，是局部和个性指标.

由样本观测值 $x_{i1},x_{i2},\cdots,x_{ip}, i=1,\cdots,n$，分别计算 $x_i$与 $x_j$之间的简单相关系数 $r_{ij}$，得自变量样本相关阵

$$\boldsymbol{r} = \left[ \begin{matrix} 1 & r_{12} & \cdots & r_{1p} \\ r_{21} & 1 & \cdots & r_{2p} \\ \vdots & \vdots & & \vdots \\ r_{p1} & r_{p2} & \cdots & 1 \end{matrix} \right]$$
注意相关阵是对称矩阵。
记 $\boldsymbol{X}^* = (x_{ij}^*)_{n \times p}$表示中心标准化的设计阵，则相关阵可表示为 $$\boldsymbol{r} = (\boldsymbol{X}^*)'\boldsymbol{X}^*$$ 进一步求出 $y$与每个自变量 $x_i$的相关系数 $r_{yi}$，得增广的样本相关阵为
$$\check{\boldsymbol{r}} = \left[ \begin{matrix} 1 & r_{y1} & r_{y2} & \cdots & r_{yp} \\ r_{1y} & 1 & r_{12} & \cdots & r_{1p} \\ r_{2y} & r_{21} & 1 & \cdots & r_{2p} \\ \vdots & \vdots & \vdots & & \vdots \\ r_{py} & r_{p1} & r_{p2} & \cdots & 1 \end{matrix} \right]$$

这里不介绍 偏决定系数了，感兴趣的读者可以自行百度学习

在多元线性回归分析中，当其他变量被固定后，给定的任两个变量之间的相关系数，叫做偏相关系数

偏相关系数可以度量 $p+1$个变量 $y,x_1,x_2,\cdots,x_p$之中任意两个变量的线性相关程度，而这种相关程度是在固定其余 $p-1$个变量的影响下的线性相关

---

R程序作多元线性回归的演示实例

这里参考一网友的多元线性回归分析的例子，http://blog.csdn.net/lance313/article/details/51241142

使用的训练数据: csv格式，含有19维特征
数据下载地址: http://pan.baidu.com/s/1eSx1fwe

数据准备

将下载好的两个csv文件放在R的工作目录下，可通过getwd()函数查看当前工作目录

rm(list = ls(all = TRUE))  #清空工作空间
library(car)
library(corrplot,quietly = TRUE)

##数据读取
name <- "vt.csv"
namepre <- "vp.csv"

#训练集
dataset <- read.csv(name,na.strings = c(".","NA","","?"),strip.white = TRUE,encoding = "UTF-8")
#预测集
datasetpre <- read.csv(namepre, na.strings = c(".","NA","","?"),strip.white = TRUE,encoding = "UTF-8")
head(datasetpre)
head(dataset)

datapre <- datasetpre[,-1]

##训练集准备
datatrain <- dataset[,-ncol(dataset)]
datatarget <- dataset$t

> head(dataset)
  v1 v2 v3 v4 v5 v6 v7 v8  v9 v10 v11 v12 v13 v14 v15 v16 v17 v18 v19    t
1  1  1  1  3  1  1  3  3  13  13  13  14  13  13  18  18  13  13  12   96
2  3  2  2  2  2  2  3  2  78  48  47  50  47  48  83  52  57  38  38  166
3  2  2  2  2  2  2  2  2  15  14  14  18  14  14  23  22  29  28  27   13
4 52 49 48 64 48 49 91 88 328 297 288 419 288 297 530 493 287 278 274 1002
5  0  0  0  0  0  0  0  0  20   6   6   6   6   6  26   7   3   2   2   10
6  0  0  0  1  0  0  1  1   1   1   1   1   1   1   1   1   1   1   1    4

> head(datasetpre)
  item_id v1 v2 v3 v4 v5 v6 v7 v8  v9 v10 v11 v12 v13 v14 v15 v16 v17 v18 v19
1     197  2  2  2  4  2  2  4  4  38  37  37  46  37  37  58  57  41  39  38
2     300  0  0  0  0  0  0  0  0   6   4   4   4   4   4   6   4  16  13  13
3     535  5  5  5  5  5  5  5  5  18  18  18  18  18  18  20  20  28  26  26
4     585  4  4  4  4  4  4  5  5  27  26  26  32  26  26  36  35  28  24  24
5     727  4  4  4  4  4  4  6  6 172 169 162 202 162 169 248 244 147 146 140
6    1765  1  1  1  2  1  1  4  4  13  13  13  14  13  13  18  17  13  13  13
> 

相关性检测

#相似矩阵
cor <- cor(dataset,use = "pairwise",method = "pearson")
cor
corrplot(cor)    #相关阵图

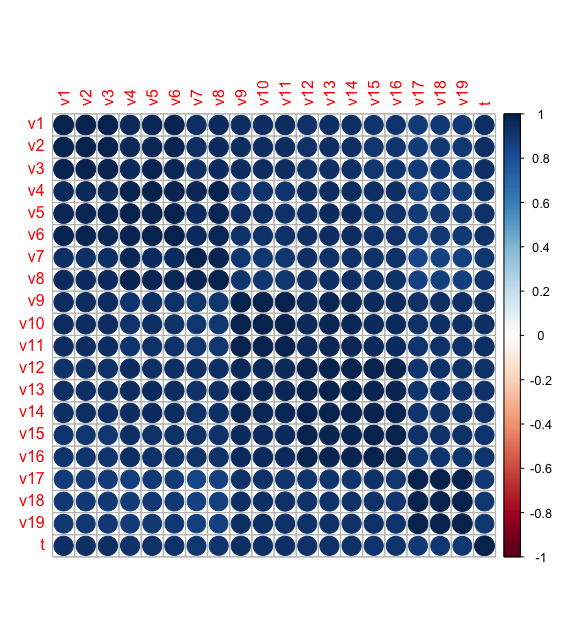
从结果可以看到，自变量之间存在非常严重的共线性，不能直接作为回归参数输入；若自变量之间的线性关系超过自变量与因变量之间的线性关系，则回归模型稳定性受到破坏.

主成分分析

利用主成分分析来确定主成分因子，从而可以去掉一些影响不大的自变量

#主成分分析
pca <- princomp(datatrain,cor = T)
summary(pca,loadings = T)
screeplot(pca,type = "lines")   #主成分分析的碎石图

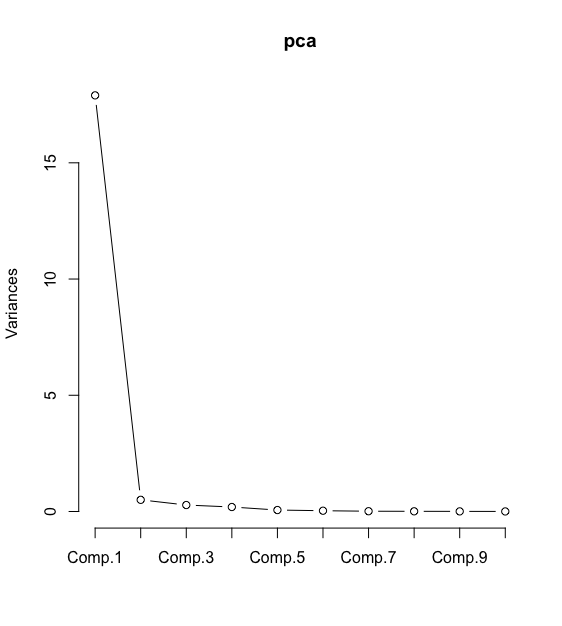
从图中可以看成，仅用两个主成分即可解释96.8%的累积误差，因此选用 Comp.1和Comp.2进行建模

#重新整理数据
loading <- as.data.frame(pca$loadings[])

comps <- as.data.frame(as.matrix(datatrain) %*% as.matrix(loading))

建立多元回归模型

> lmP <- lm(formula = dataset$t ~ comps$Comp.1+comps$Comp.2)  #利用两个主成分做多元线性回归拟合

> summary(lmP)

Call:
lm(formula = dataset$t ~ comps$Comp.1 + comps$Comp.2)

Residuals:
    Min      1Q  Median      3Q     Max 
-346.46   -7.58   -3.99    2.13  539.17 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   3.98998    3.66767   1.088  0.27753    
comps$Comp.1 -0.93848    0.08962 -10.472  < 2e-16 ***
    comps$Comp.2 -0.44861    0.14896  -3.012  0.00282 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 59.48 on 298 degrees of freedom
Multiple R-squared:  0.8913,    Adjusted R-squared:  0.8905 
F-statistic:  1221 on 2 and 298 DF,  p-value: < 2.2e-16

>

模型检验结果为:

• 拟合优度检验
  $R^2$ 为0.8905，自变量与因变量之间具有较强的线性关系
• 估计标准误差检验
  RSE值为 59.48
• 回归方程显著性检验($F$检验)
  $F$检验结果为1221，p-value < 2.2e-16，非常显著，所有自变量与因变量的线性关系密切
• 回归系数显著性检验($t$检验)
  可以看到Comp.1，Comp.2的p-value均小于0.05，表明这两个自变量对模型影响显著

多重共线性检验

> #多重共线性检验
> compsx <- comps[c("Comp.1","Comp.2")]
> x <- cor(compsx,use = "pairwise",method = "pearson")
> kappa(x)
[1] 172.2621
> 

可以看到，kappa值等于172，任具有较强的多重共线性，因为 k < 100，可认为不存在多重共线性

逐步回归

可进一步利用step函数选取精简变量，从而消除多重共线性的影响

> step(lmP)
Start:  AIC=2462.52
dataset$t ~ comps$Comp.1 + comps$Comp.2

               Df Sum of Sq     RSS    AIC
<none>                      1054211 2462.5
- comps$Comp.2  1     32084 1086295 2469.5
    - comps$Comp.1  1    387936 1442147 2554.8

Call:
lm(formula = dataset$t ~ comps$Comp.1 + comps$Comp.2)

Coefficients:
 (Intercept)  comps$Comp.1  comps$Comp.2  
      3.9900       -0.9385       -0.4486  

> 

发现回归方程并没有改善，需要进行残差分析看看

残差分析

> #残差分析
> par(mfrow = c(2,2))
> plot(lmP)
> 

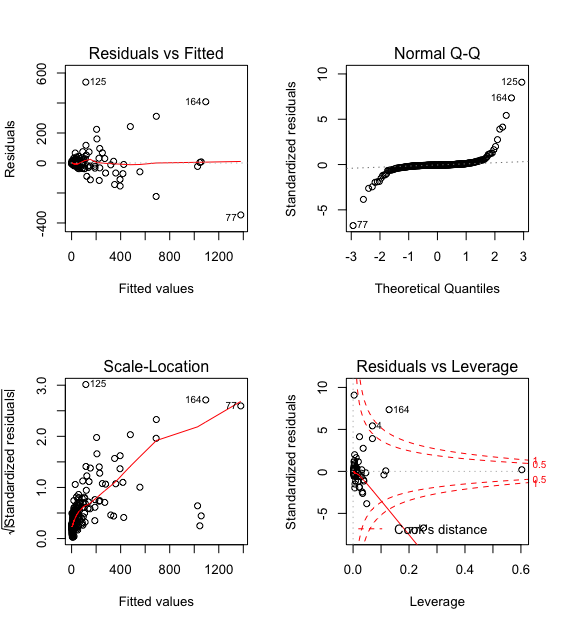
预测

comppre <- as.data.frame(as.matrix(datapre) %*% as.matrix(loading))[c(1,2,3)]

coe <- as.matrix(lmP$coefficients)
tpre <- as.matrix(comppre) %*% coe
output <- data.frame(datasetpre[,1],as.data.frame(tpre))