机器学习篇

高斯判别分析

简介

高斯判别分析（Gaussian discriminative analysis）是一个较为直观的模型，基本的假设是我们得到的数据是独立同分布的(IID)，虽然在实际中这种假设很难达到，但有时候拥有了好的假设可以得到较好的结果。

在Andrew Ng大神的CS229 Lecture notes中有一个例子：
假设我们要对大象和狗分类，回归模型和感知机模型是在两类数据之间找到一个判决边界(decision boundary)，通过这个decision boundary来区分大象和狗。

高斯判别分析提供了另外一种思路：
首先我们观察大象，对大象建立一个模型来描述他的特点；
再观察狗，并建立相应的模型来描述狗。
当一个新的狗或者象过来时，我们首先带入象模型和狗模型，对比两者的满足不同模型的概率，最后决定新来的的动物的类别。

---

多元高斯分布

我们处理的数据往往是多维了，因此高斯分布也应该是多维的。

我们先回顾一下一维正态分布:

$$f(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp{-\frac{(x-\mu)^2}{2\sigma^2}}$$ 其中，$x$ 为样本特征，$\sigma$ 标准差，$\mu$ 为样本期望值；
该分布通常记为: $N(\mu,\sigma^2)$，当 $\mu = 0,\sigma = 1$ 时的正态分布是标准正态分布.

正态分布: https://baike.baidu.com/item/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83/829892?fr=aladdin

正态分布也叫高斯分布.

那么，$n$ 维正态分布表示为:

$$p(x;\mu,\Sigma) = \frac{1}{(2\pi)^{n/2} |\Sigma|^{1/2}} \exp{\left(-\frac{1}{2} (x-\mu)^T \Sigma^{-1} (x - \mu) \right)}$$ 其中，$p(x;\mu,\Sigma)$ 中的 $;$ 后面的 $\mu,\Sigma$ 表示参数，该式表示以 $\mu \in R^n$ 为均值，$\Sigma \in R^{n*n}$ 为协方差的 $n$ 维正态分布.

协方差: https://www.zhihu.com/question/20852004

协方差矩阵: https://baike.baidu.com/item/%E5%8D%8F%E6%96%B9%E5%B7%AE%E7%9F%A9%E9%98%B5/9822183

当 $\mu$ 是二维的时候可以如下图表示:

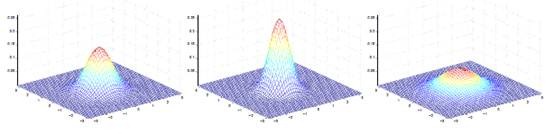
其中 $\mu$ 决定中心位置，$\Sigma$ 决定投影椭圆的朝向和大小。

如下图:

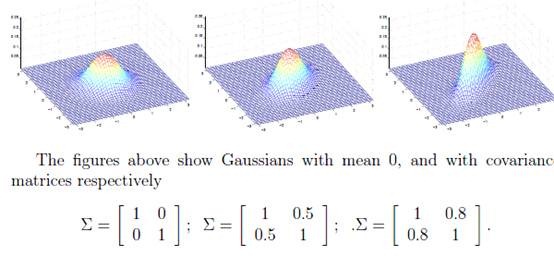
对应的 $Sigma$ 都不同。

---

模型描述

将 $n$ 维高斯模型应用到监督学习中，假设输入数据为 $x$，输出类别为 $y \in \{0,1\}$，那么对应的二分类问题描述为:

$$\begin{array} & y &\approx& Bernoulli(\phi) \\ x|y = 0 &\approx& \cal{N}(\mu_0,\Sigma) \\ x|y = 1 &\approx& \cal{N}(\mu_1,\Sigma) \end{array}$$

其中，$Bernoulli(\phi)$ 表示伯努利分布，其表达式为:

$$f(x|p) = \begin{cases} p^{x} (1 - p)^{1-x}, & x = 0,1 \\ 0, & x \neq 0,1 \end{cases}$$
这里的 $p$ 表示 $x = 1$ 这个事件发生的概率.

这就是经典的高斯判别分析模型。

伯努利分布: https://baike.baidu.com/item/%E4%BC%AF%E5%8A%AA%E5%88%A9%E5%88%86%E5%B8%83/7167021?fr=aladdin

类别 $y$ 服从伯努利分布；当 $y=0$ 时，$x$ 服从均值为 $\mu_0$，协方差矩阵为 $\Sigma$ 的多元高斯分布.

这里假设 $y=0$ 和 $y=1$ 时 $x$ 服从的多元高斯分布的协方差相同；

事实上这两者不一样模型会更精确，不过为了简化我们这里假设一样；另外如果样本量比较少，不同的 $\Sigma$ 会使算法不稳定，因为过少的样本甚至导致协方差矩阵不可逆.

于是上面的表达式更直观的表述为:

$$\begin{array} & p(y) &=& \phi^y (1 - \phi)^{1 - y} \\ p(x|y=0) &=& \frac{1}{(2\pi)^{n/2} |\Sigma|^{1/2}} \exp{\left(-\frac{1}{2} (x-\mu_0)^T \Sigma^{-1} (x - \mu_0) \right)} \\ p(x|y=1) &=& \frac{1}{(2\pi)^{n/2} |\Sigma|^{1/2}} \exp{\left(-\frac{1}{2} (x-\mu_1)^T \Sigma^{-1} (x - \mu_1) \right)} \end{array}$$

通过贝叶斯公式求出一个样本分别属于两类的概率，进而可实现对该样本的分类:

$$\begin{array} & p(y|x) &=& \frac{p(x|y)p(y)}{p(x)} \\ y &=& arg \ \max_{y} p(y|x) \\ &=& arg \ \max_{y} \frac{p(x|y)p(y)}{p(x)} \\ &=& arg \ \max_{y} p(x|y)p(y) \end{array}$$

用高斯判别分析做分类，其实就是为了学习这其中的几个参数 $\phi,\mu_0,\mu_1,\Sigma$，下面我们先直接给出学习公式，在下一节中我们会详细的推导出这些学习公式.

可以直观的求解：每个数据的类别已经知道，并且每一组别的数据分布都是高斯分布，我们可以直接用高斯分布的参数估计来求解这几个未知参数

我们知道高斯分布的均值的估计就是数据的均值，那么

$$\begin{array} & \mu_0 &=& \frac{\sum_{i=1}^m I(y^(i) = 0) x^{(i)}}{\sum_{i=1}^m I(y^(i) = 0)} \\ \mu_1 &=& \frac{\sum_{i=1}^m I(y^(i) = 1) x^{(i)}}{\sum_{i=1}^m I(y^(i) = 1)} \end{array}$$

其中，$I(x) = \begin{cases} 1, & x \in \omega \\ 0, & x \notin \omega \end{cases}$，$\omega$ 为给定的条件或者是集合.

如果两个高斯分布用同一个 $\Sigma$，则:

$$\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)} - \mu_{y^{(i)}})(x^{(i)} - \mu_{y^{(i)}})^T$$
否则，分布求取每个类别的方差即可。

还有一个参数 $\phi$，直接统计点的个数可得到:

$$\phi = \frac{1}{m} \sum_{i=1}^m I(y^{(i)} = 1)$$

这就是 GDA 的思路和实现方式，通过上面的几个参数的计算公式就可以得到高斯判别分析模型；当有新的样本点进来是，就可以通过 $p(y|x;\phi,\mu_0,\mu_1,\Sigma)$ 计算出相应的概率，然后取最大的那个所对应的类别即可。

---

算法推导

使用最大似然估计应用到目标函数上，对未知量 $\phi,\mu_0,\mu_1,\Sigma$ 进行估计。

其对数似然函数为:

$$\begin{aligned} l(\phi,\mu_0,\mu_1,\Sigma) &= \log{\prod_{i=1}^m{p(x^{(i)},y^{(i)})}} = \log{\prod_{i=1}^m{p(x^{(i)}|y^{(i)})p(y^{(i)})}} \\ &= \sum_{i=1}^m{\log\;p(x^{(i)}|y^{(i)})}+\sum_{i=1}^m{\log\;p(y^{(i)})} \\ &= \sum_{i=1}^m{\log\;(p(x^{(i)}|y^{(i)}=0)^{1-y^{(i)}}*p(x^{(i)}|y^{(i)}=1)^{y^{(i)}})} + \sum_{i=1}^m{\log\;p(y^{(i)})} \\ &= \sum_{i=1}^m{(1-y^{(i)}) \log\;p(x^{(i)}|y^{(i)}=0)} + \sum_{i=1}^m{{y^{(i)}} \log\;p(x^{(i)}|y^{(i)}=1)}+\sum_{i=1}^m{\log\;p(y^{(i)})} \end{aligned}$$

其中上述第二行式子到第三行，只是将 $p(x^{(i)} | y^{(i)})$ 展开了而已，因为 $y \in \{0,1\}$，所以 $p(x^{(i)} | y^{(i)})$ 可按 $y^{(i)}$ 的值分开来考虑；

注意此函数第一部分只和 $\mu_0,\Sigma$ 有关，第二部分只和 $\mu_1,\Sigma$ 有关，第三部分只和 $\phi$ 有关。

最大化该函数，首先对 $\phi$ 求偏导，令其等于零:

$$\begin{aligned} \frac{\partial\;l(\phi,\mu_0,\mu_1,\Sigma)}{\partial\phi}&=\frac{\sum_{i=1}^m{log\;p(y^{(i)})}}{\partial\phi} \\&= \frac{\partial\sum_{i=1}^m{log\;\phi^{y^{(i)}}(1-\phi)^{1-y^{(i)}})}}{\partial\phi} \\&=\frac{\partial\sum_{i=1}^m{y^{(i)}\;log\;\phi+(1-y^{(i)})log(1-\phi)}}{\partial\phi} \\&=\sum_{i=1}^m{(y^{(i)}\frac{1}{\phi}-(1-y^{(i)})\frac{1}{1-\phi})} \\&= \sum_{i=1}^m \left( \left( I(y^{(i)} = 0) \frac{1}{\phi} -(1 - I(y^{(i)} = 0)) \frac{1}{1 - \phi} \right) + \left( I(y^{(i)} = 1) \frac{1}{\phi} -(1 - I(y^{(i)} = 1)) \frac{1}{1 - \phi} \right) \right) \\&=\sum_{i=1}^m{(I(y^{(i)}=1)\frac{1}{\phi}-I(y^{(i)}=0)\frac{1}{1-\phi})} \end{aligned}$$

其中第四行到第五行的式子，同样是按照 $y^{(i)} = 0$ 和 $y^{(i)} = 1$ 展开分别考虑，而又因为 $I(y^{(i)} = 0) = 0$，所以从第五行式子得到了第六行式子.

令上式偏导为零，可求解出 $\phi$ :

$$\begin{aligned} \phi=\frac{I(y^{(i)}=1)}{I(y^{(i)}=0)+I(y^{(i)}=1)}=\frac{I(y^{(i)}=1)}{m}\end{aligned}$$

同样的，对 $\mu_0$ 求偏导为:

$$\begin{aligned} \frac{\partial\;l(\phi,\mu_0,\mu_1,\Sigma)}{\partial\mu_0}&=\frac{\partial\sum_{i=1}^m{(1-y^{(i)})log\;p(x^{(i)}|y^{(i)}=0)}}{\partial\mu_0} \\ &= \frac{\partial \sum_{i=1}^m (1 - y^{(i)}) \log\; \left\{ \frac{1}{(2\pi)^{n/2} |\Sigma|^{1/2}} \exp{\left(-\frac{1}{2} (x-\mu_0)^T \Sigma^{-1} (x - \mu_0) \right)} \right\}}{\partial \mu_0} \\&=\frac{\partial\sum_{i=1}^m{(1-y^{(i)})(log\frac{1}{\sqrt{(2\pi)^n|\Sigma|}}-\frac{1}{2}(x^{(i)}-\mu_0)^T\Sigma^{-1}(x^{(i)}-\mu_0))}}{\partial\mu_0} \\&=\sum_{i=1}^m{(1-y^{(i)})(\Sigma^{-1}(x^{(i)}-\mu_0))} \\&=\sum_{i=1}^m{I(y^{(i)}=0)\Sigma^{-1}(x^{(i)}-\mu_0)} \end{aligned}$$

其中第一行到第二行，是应用了 $p(x^{(i)}|y^{(i)} = 0)$ 服从多元高斯分布；第二行到第三行是简单的对数运算；第三行到第四行是对 $\mu_0$ 求偏导，这里 $\frac{\partial \frac{1}{2}(x^{(i)}-\mu_0)^T\Sigma^{-1}(x^{(i)}-\mu_0)}{\partial \mu_0} = -\Sigma^{-1}(x^{(i)}-\mu_0)$ ，这有点类似于与一元高斯分布时，$\frac{\partial \frac{1}{2} \sigma(x^{(i)}-\mu_0)^2}{\partial \mu_0} = -\sigma(x^{(i)}-\mu_0)$ .

令其等于零，可解得:

$$\begin{aligned} \mu_0=\frac{\sum_{i=1}^m{I(y^{(i)}=0)x^{(i)}}}{\sum_{i=1}^m{I(y^{(i)}=0)}} \end{aligned}$$

根据对称性，可直接得出:

$$\begin{aligned} \mu_1=\frac{\sum_{i=1}^m{I(y^{(i)}=1)x^{(i)}}}{\sum_{i=1}^m{I(y^{(i)}=1)}} \end{aligned}$$

下面对 $\Sigma$ 求偏导数，由于似然函数只有前面两部分与 $\Sigma$ 有关，则将前面两部分改写如下:

$$\begin{aligned} &\sum_{i=1}^m{(1-y^{(i)})log\;p(x^{(i)}|y^{(i)}=0)}+\sum_{i=1}^m{{y^{(i)}}log\;p(x^{(i)}|y^{(i)}=1)}\\&= \sum_{i=1}^m{(1-y^{(i)})(log\frac{1}{\sqrt{(2\pi)^n|\Sigma|}}-\frac{1}{2}(x^{(i)}-\mu_0)^T\Sigma^{-1}(x^{(i)}-\mu_0))} \\&+ \sum_{i=1}^m{{y^{(i)}}(log\frac{1}{\sqrt{(2\pi)^n|\Sigma|}}-\frac{1}{2}(x^{(i)}-\mu_1)^T\Sigma^{-1}(x^{(i)}-\mu_1))}\\&=\sum_{i=1}^m{log\frac{1}{\sqrt{(2\pi)^n|\Sigma|}}}-\frac{1}{2}\sum_{i=1}^m{(x^{(i)}-\mu_{y^{(i)}})^T\Sigma^{-1}(x^{(i)}-\mu_{y^{(i)}})}\\&=\sum_{i=1}^m{(-\frac{n}{2}log(2\pi)-\frac{1}{2}log(|\Sigma|))}-\frac{1}{2}\sum_{i=1}^m{(x^{(i)}-\mu_{y^{(i)}})^T\Sigma^{-1}(x^{(i)}-\mu_{y^{(i)}})} \end{aligned}$$

这其中也只是一些简单的对数运算，看懂难度不大。

于是我们整理出与 $\Sigma$ 有关的项，然后对 $\Sigma$ 求偏导，并令其等于零:

$$\begin{aligned} \frac{\partial\;l(\phi,\mu_0,\mu_1,\Sigma))}{\partial\Sigma} &= \frac{-\frac{1}{2}\sum_{i=1}^m \log{(|\Sigma|)} - \frac{1}{2} \sum_{i=1}^m{(x^{(i)}-\mu_{y^{(i)}})^T\Sigma^{-1}(x^{(i)}-\mu_{y^{(i)}})}}{\partial \Sigma} \\&=-\frac{1}{2}\sum_{i=1}^m(\frac{1}{|\Sigma|}|\Sigma|\Sigma^{-1})-\frac{1}{2}\sum_{i=1}^m(x^{(i)}-\mu_{y^{(i)}})(x^{(i)}-\mu_{y^{(i)}})^T\frac{\partial\Sigma^{-1}}{\partial\Sigma}\\&=-\frac{m}{2}\Sigma^{-1}-\frac{1}{2}\sum_{i=1}^m(x^{(i)}-\mu_{y^{(i)}})(x^{(i)}-\mu_{y^{(i)}})^T(-\Sigma^{-2})) \end{aligned}$$

这其中用到了:

$$\begin{aligned} \frac{\partial|\Sigma|}{\partial\Sigma}=|\Sigma|\Sigma^{-1} \\ \begin{aligned} \frac{\partial\Sigma^{-1}}{\partial\Sigma}=-\Sigma^{-2}\end{aligned} \end{aligned}$$

这里的矩阵对矩阵求导，只要会用就行了，不用深究，或者读者可以自己查阅相关的数学资料.

令其为零，求得:

$$\begin{aligned} \Sigma=\frac{1}{m}\sum_{i=1}^m(x^{(i)}-\mu_{y^{(i)}})(x^{(i)}-\mu_{y^{(i)}})^T\end{aligned}$$

可以看到上面推出来的各个参数的式子与上一节中给出的一致。

---

与逻辑回归的关系

根据上面的结果以及贝叶斯公式，可有:

$$\begin{aligned} p(y=1|x)&=\frac{p(x|y=1)p(y=1)}{p(x)} \\&=\frac{N(\mu_1,\Sigma)\phi}{N(\mu_0,\Sigma)(1-\phi)+N(\mu_1,\Sigma)\phi}\\&=1/{(1+\frac{N(\mu_0,\Sigma))}{N(\mu_1,\Sigma)}\frac{1-\phi}{\phi})} \end{aligned}$$

而:

$$\begin{aligned} \frac{N(\mu_0,\Sigma)}{N(\mu_1,\Sigma)}&= exp\{(x-\mu_0)^T\Sigma^{-1}(x-\mu_0)-(x-\mu_1)^T\Sigma^{-1}(x-\mu_1)\}\\&=exp\{ 2(\mu_1-\mu_0)^T\Sigma^{-1}x+(\mu_0^T\Sigma\mu_0-\mu_1^T\Sigma\mu_1)\}\end{aligned}$$

那么令:

$$\begin{aligned} 2\Sigma^{-1}(\mu_1-\mu_0) =(\theta_1,\theta_2,...,\theta_n)^T\\ \theta_0=\mu_0^T\Sigma\mu_0-\mu_1^T\Sigma\mu_1+log\frac{1-\phi}{\phi}\\ \end{aligned}$$

于是有:

$$\begin{aligned} p(y=1|x)=\frac{1}{1+exp(\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n)} \end{aligned}$$

这就是逻辑回归的形式了。

在推导逻辑回归的时候，我们并没有假设类内样本是服从高斯分布的，因而GDA只是逻辑回归的一个特例，其建立在更强的假设条。故两者效果比较：

• 逻辑回归是基于弱假设推导的，则其效果更稳定，适用范围更广

• 数据服从高斯分布时，GDA效果更好

• 当训练样本数很大时，根据中心极限定理，数据将无限逼近于高斯分布，则此时GDA的表现效果会非常好

---

R 代码示例

R版本的高斯判别分析笔者没找到对应的包，所以自己根据上面的参数估计公式写了一个:

# 构造数据 x
data = c(0.230000, 0.394000, 
         0.238000, 0.524000,  
         0.422000, 0.494000,  
         0.364000, 0.556000,  
         0.320000, 0.448000,  
         0.532000, 0.606000,  
         0.358000, 0.660000,  
         0.144000, 0.442000,  
         0.124000, 0.674000,  
         0.520000, 0.692000,  
         0.410000, 0.086000,  
         0.344000, 0.154000,  
         0.490000, 0.228000,  
         0.622000, 0.366000,  
         0.390000, 0.270000,  
         0.514000, 0.142000,  
         0.616000, 0.180000,  
         0.576000, 0.082000,  
         0.628000, 0.286000,  
         0.780000, 0.282000)
x = matrix(data,ncol = 2,byrow = T)
dim(x)
head(x)
# 表示一个样本有两个特征
x1 = x[,1]
x2 = x[,2]
# 对应的类别 y，这里设置为两类
y = matrix(rep(c(0,1),each = 10))
dim(x)
# 参数估计
sum0 = sum(1 - y)
sum1 = sum(y)
phi = sum1/(sum0 + sum1) # 估计出类别y 的伯努利分布参数phi
# 类别0 的期望均值，类别1 的期望均值
mu0 = c(  t(1 - y) %*% x1/sum0 ,  t(1 - y) %*% x2/sum0 )
mu1 = c( t(y) %*% x1/sum1, t(y) %*% x2/sum1 )
#协方差
sigma = cov(x1,x2)
# 根据 p(y)*p(x|y) 来进行判别
evalutor_p <- function(x){
  n = length(x)
  py0 = phi^0 * (1 - phi)^(1 - 0)
  py1 = phi^1 * (1 - phi)^(1 - 1)
  px0 = 1/((2*pi)^(n/2) * sigma^(1/2)) * exp(-1/2 * sigma * t(matrix(x - mu0)) %*% matrix(x-mu0))
  px1 = 1/((2*pi)^(n/2) * sigma^(1/2)) * exp(-1/2 * sigma * t(matrix(x - mu1)) %*% matrix(x-mu1))
  # 比较分别属于不同类别的概率，取最大的
  ifelse(py0*px0 > py1*px1,0,1)
}
#测试
testx <- c(0.780000, 0.282000)
evalutor_p(testx)

测试的输出结果为类别 1 ，预测正确.

小结

高斯判别法也是一种线性分类器，到这里就讲完了，希望对读者有帮助。

参考

• https://www.cnblogs.com/jcchen1987/p/4424436.html
• https://www.cnblogs.com/taokongcn/p/4117413.html
• http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971903.html
• http://blog.csdn.net/u013571752/article/details/23665239