时间序列篇

时间序列预处理

时间序列的定义

在统计研究中，常用按时间顺序排列的一组随机变量

$$X_1,X_2,\cdots,X_t,\cdots$$ 来表示一个随机事件的时间序列，简记为$\{X_t,t \in T\}$或$\{ X_t \}$

用

$$x_1,x_2,\cdots,x_n$$ 或$\{x_t, t = 1,2,\cdots,n\}$表示该随机序列的n个有序观察值，称为序列长度为 $n$ 的观察值序列.

在日常生活中，观察值序列比比皆是。比如把全国1999-2008年普通高等学校每年的招生人数按照时间顺序记录下来，就构成了一个序列长度为 10 的全国普通高等学校招生人数时间序列(单位: 万人):

$$159.7,220.6,268.3,320.5,382.2,447.3,504.5,546.1,565.9,607.7$$

我们进行时序研究的目的是想揭示随机时序$\{X_t\}$的性质，而要实现这个目标就要分析它的观察值序列$\{x_t\}$的性质，由观察值序列的性质来推断随机时序$\{X_t\}$的性质.

---

平稳时间序列

拿到一个观察值序列之后，首先要对它的平稳性和纯随机性进行检验，这两个重要的检验称为序列的预处理.根据检验的结果可以将序列分为不同的类型，对不同类型的序列我们会采用不同的分析方法.

特征统计量

一种简单、实用的描述时间序列统计特征的方法是研究该序列的低阶矩.特别是均值、方差、自协方差和自相关系数，我们也称为特征统计量.

尽管这些统计量不能描述随机序列全部的统计性质，但由于它们概率意义明显，易于计算，而且往往能代表随机序列的主要概率特征，所以我们对时间序列进行分析，主要就是通过分析这些特征量的统计特性，推断出随机序列的性质.

均值

对时间序列 $\{X_t,t \in T\}$而言，任意时刻的序列值 $X_t$ 都是一个随机变量，都有它自己的概率分布，不妨记 $X_t$ 的分布函数为 $F_t(x)$.

只要满足条件

$$\int_{-\infty}^{\infty} xd{F_t(x)} < \infty$$ 就一定存在某个常数 $\mu_t$，使得随机变量 $X_t$总是围绕在常数值 $\mu_t$ 附近做随机波动.我们称 $\mu_t$为序列 $\{ X_t \}$在 $t$ 时刻的均值函数. $$\mu_t = E(X_t) = \int_{-\infty}^{\infty} xd{F_t(x)}$$ 当 $t$ 取遍所有的观察时刻时，就得到一个均值函数序列 $\{\mu_t,t \in T\}$.它反映的是时间序列 $\{X_t,t \in T\}$每时每刻的平均水平.

---

方差

当 $\int_{-\infty}^{\infty}x^2d{F_t(x)} < \infty$ 时，可以定义时间序列的方差函数用以描述序列值围绕其均值做随机波动时的平均波动程度.

$$\sigma_t^2 = D(X_t) = E(X_t - \mu_t)^2 = \int_{-\infty}^{\infty}(x - \mu_t)^2 d{F_t(x)}$$ 同样，当 $t$ 取遍所有的观察时刻时，我们得到一个方差函数序列 $\{ \sigma_t^2, t \in T\}$.

---

自协方差函数和自相关系数

类似于协方差函数和相关系数的定义，在时间序列分析中我们定义了自协方差函数(autocovariance function)和自相关系数(autocorrelation coefficient)的概念.

对于时间序列 $X_t, t \in T$，任取 $t,s \in T$，定义 $\gamma(t,s)$为序列 $\{X_t\}$的自协方差函数:

$$\gamma(t,s) = E[(X_t - \mu_t)(X_s - \mu_s)]$$ 定义 $\rho(t,s)$为时间序列 $\{X_t\}$的自相关系数，简记为 $ACF$. $$\rho(t,s) = \frac{\rho(t,s)}{\sqrt{D(X_t)\times D(X_s)}}$$ 之所以称它们为自协方差函数和自相关系数，是因为通常的协方差函数和相关系数度量的是两个不同事件在两个不同时期之间的相关程度，形象地讲就是度量自己过去的行为对自己现在的影响.

---

宽平稳

宽平稳(weak stationary)是使用序列的特征统计量来定义的一种平稳性.他认为序列的统计性质主要由它的低阶矩决定，所以只要保证序列低阶矩(二阶)平稳，就能保证序列的主要性质近似稳定.

如果 $\{X_t\}$满足如下三个条件:

1. 任取 $t \in T$，有 $E(X_t^2) < \infty$

2. 任取 $t \in T$，有 $E(X_t) = \mu$，$\mu$为常数

3. 任取 $t,s,k \in T$，且 $k+s-t \in T$，有 $\gamma(t,s) = \gamma(k,k+s-t)$

则称 $\{X_t\}$为宽平稳时间序列.宽平稳也称为弱平稳或二阶平稳(second-order stationary).

所谓严平稳(strictly stationary)是一种条件比较苛刻的平稳性定义，它认为只有当序列所有的统计性质都不会随着时间的推移而发生变化时，该序列才能被认为是平稳的.

显然，严平稳比宽平稳的条件严格.所以后面我们讨论的时候都是要求时间序列满足宽平稳就可以了.

平稳时间序列的统计性质

常数均值

$$E(X_t) = \mu, \forall t \in T$$

自协方差函数和自相关系数只依赖于时间的平移长度,而与时间的起始点无关

$$\gamma(t,s) = \gamma(k,k+s-t), \forall t,s,k \in T$$ 根据这个性质，可以将自协方差函数由二维函数 $\gamma(t,s)$简化为一维函数 $\gamma(s-t)$: $$\gamma(s-t) \hat{=} \gamma(t,s)，\forall t,s \in T$$ 也由此引出了延迟$k$自协方差函数的概念.

对于平稳时间序列 $\{X_t,t \in T\}$，任取 $t (t+k \in T)$，定义 $\gamma(k)$为时间序列 $\{X_t\}$的延迟$k$自协方差函数:

$$\gamma{k} = \gamma(t,t+k)$$

同样根据平稳序列的这个性质，容易推断出平稳随机序列一定具有常数方差:

$$D(X_t) = \gamma(t,t) = \gamma(0), \forall \in T$$ 由延迟 $k$自协方差函数的概念可以等价得到延迟 $k$自相关系数的概念: $$\rho_k = \frac{\gamma(t,t+k)}{\sqrt{D(X_t) \times D(X_{t+k})}} = \frac{\gamma(k)}{\gamma(0)}$$ 容易验证和相关系数一样，自相关系数具有如下三个性质:

1. 规范性

   $$\rho_0 = 1 且 |\rho_k| \leq 1, \forall k$$

2. 对称性

   $$\rho_k = \rho_{-k}$$

3. 非负定性
   对任意正整数 $m$，相关阵 $\Gamma_m$为对称非负定阵.

   $$\Gamma_m = \left[\begin{matrix} \rho_0 & \rho_1 & \cdots & \rho_{m-1} \\ \rho_1 & \rho_0 & \cdots & \rho_{m-2} \\ \vdots & \vdots & \ddots & \vdots \\ \rho_{m-1} & \rho_{m-2} & \cdots & \rho_0 \\ \end{matrix} \right]$$ 值得注意的是，$\rho_k$除了具有上述三个性质外，还具有一个特别的性质: 对应模型的非唯一性.

一个平稳时间序列一定唯一决定了它的自相关函数，但一个自相关函数未必唯一对应一个平稳时间序列.我们在后面的篇幅中将证明这一点.这个性质就给我们根据样本的自相关系数的特点来确定模型增加了一定的难度.

---

时序图与自相关图

时序图

所谓时序图，就是一个二维平面坐标图，通常横轴表示时间，纵轴表示序列取值.

时序图可以帮助我们直观地掌握时间序列的一些基本分布特性.所以时序分析的第一步通常是绘制时序图.

以1884-1890年英格兰和威尔士地区小麦平均亩产量数据为例，绘制时序图:

#数据准备
> yield <- c(15.2,16.9,15.3,14.9,15.7,15.1,16.7)

#生成时间序列对象
> yield <- ts(yield, start = 1884)

#绘制时序图
> plot(yield)
> 

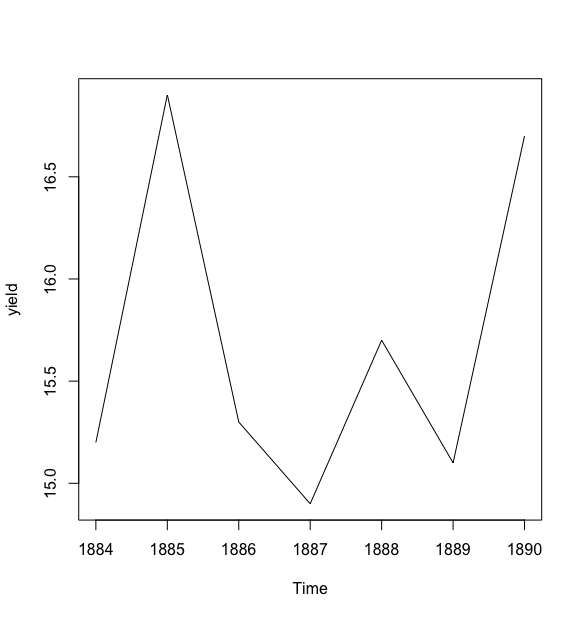
关于绘图参数的设置，读者可以参考R语言基础篇中的绘图部分

序列自相关图

自相关图示一个平面二维坐标悬垂线图.横坐标表示延迟时期数，纵坐标表示自相关系数.悬垂线表示自相关系数的大小.

依然以英格兰和威尔士地区小麦平均亩产量数据为例，继续绘制序列的自相关图

#绘制序列自相关图
> acf(yield)
>

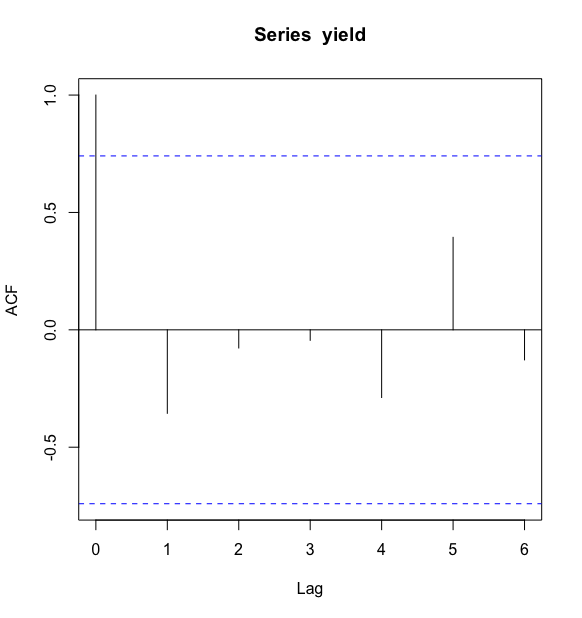
平稳性检验

对序列的平稳性有两种检验方法，一种是根据时序图和自相关图显示的特征作出判断的图检验方法；一种是构造检验统计量进行假设检验的方法.

时序图检验

根据平稳时间序列均值、方差为常数的性质，平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动，而且波动的范围有界.

如果序列的时序图显示出该序列有明显的趋势性或周期性，那么它通常不是平稳序列.根据这个性质，对于很多非平稳序列，可以通过查看它的时序图将其识别出来.

例1: 绘制1964-1999年中国纱年产量序列时序图

#读取数据
> sha <- read.table("data/file4.csv",sep = ",",header = T)

#生成时间序列对象
> output <- ts(sha$output, start = 1964)

#绘制时序图
> plot(output)
>

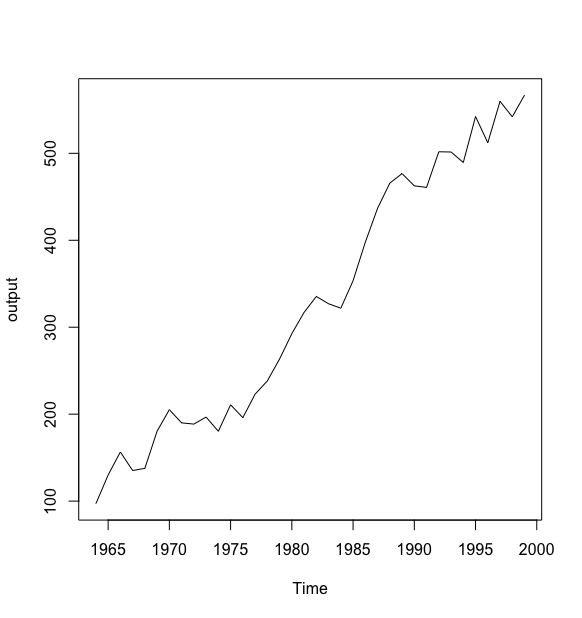
例1中的时序图显示中国纱年产量序列有明显的递增趋势，所以它一定不是平稳序列.

---

例2: 绘制1962年1月至1975年12月平均每头奶牛月产奶量序列的时序图

> a <- read.table("data/file5.csv",sep = ",", header = T)

> milk <- ts(a$milk, start = c(1962,1), frequency = 12)

> plot(milk)
>

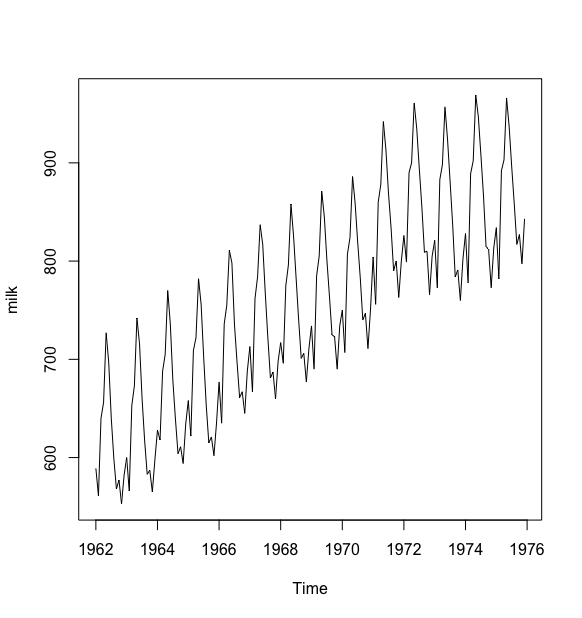
例2中的时序图清晰的显示平均每头奶牛的月产奶量以年为周期呈现出规则的周期性，除此之外，还有明显的逐年递增趋势.显然该序列也一定不是平稳序列.

---

例3: 绘制1949-1998年北京市每年最高气温序列的时序图

> b <- read.table("data/file6.csv", sep = ",", header = T)

> temp <- ts(b$temp, start = 1949)

> plot(temp)
>

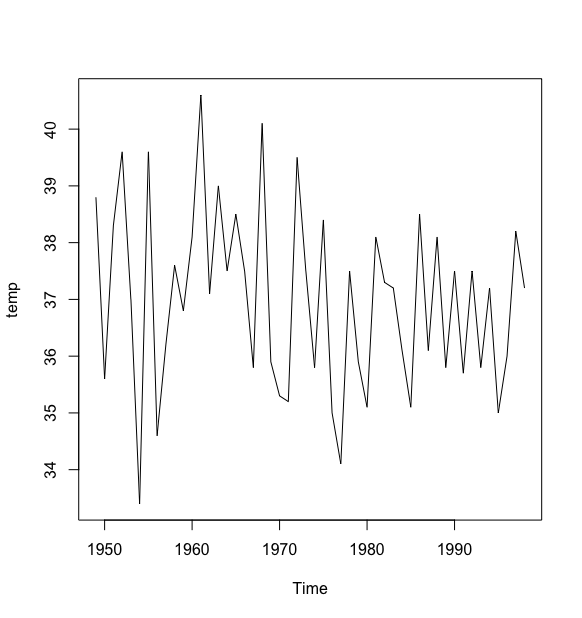
例3中的时序图显示北京市每年的最高气温始终围绕在$37^。C$附近随机波动，没有明显的趋势或周期，基本可以视为平稳序列.不过为了稳妥起见，我们还是需要利用自相关图进一步辅助识别.

---

自相关图检验

在后面的章节我们会证明平稳序列通常具有短期相关性.该性质用自相关系数来描述就是随着延迟数 $k$ 的增加，平稳序列的自相关系数 $\hat{\rho}_k$ 会很快地衰减向零.反之，非平稳序列的自相关系数 $\hat{\rho}_k$衰减向零的速度通常比较慢，这就是我们利用自相关图进行平稳性判断的标准.

例1: 以中国纱年产量序列为例

> acf(output, lag = 25)
>

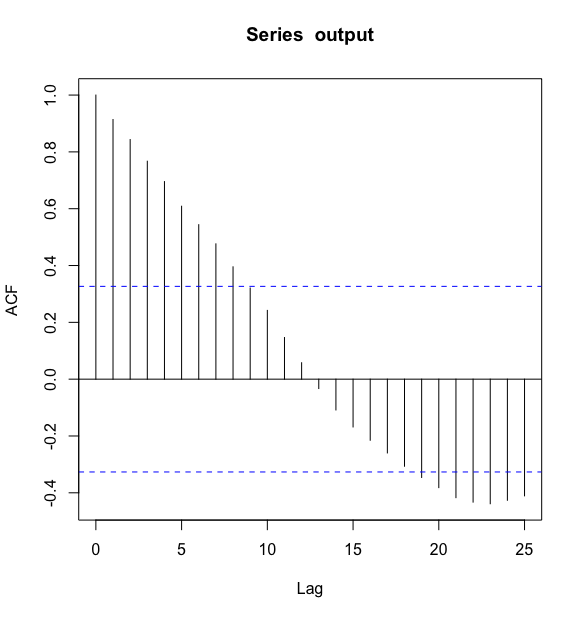
从图中我们看到序列的自相关系数衰减到零的速度相当缓慢，在很长的延迟时期里，自相关系数一直为正，而后又一直为负，在自相关图上显示出明显的三角对称性，这是具有单调趋势的非平稳序列的一种典型的自相关图形式.这和该序列的时序图显示的显著的单调递增性是一致的.

---

例2: 以奶牛的月产奶量序列绘制自相关图

> acf(milk)
>

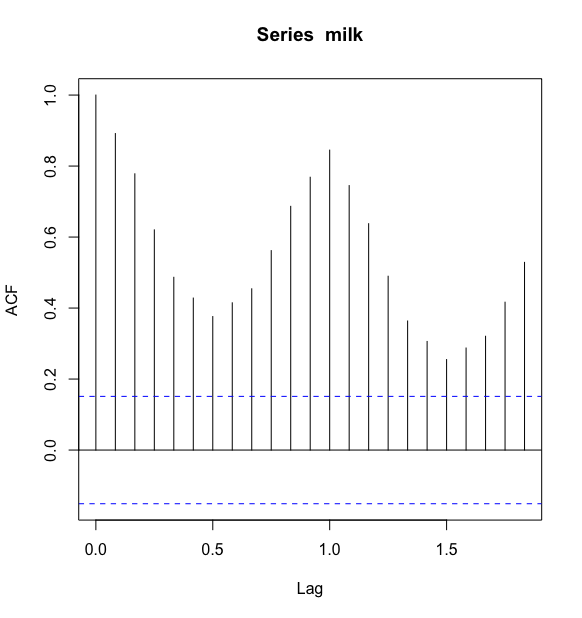
自相关图呈现序列自相关系数长期位于零轴的一边，这是具有单调趋势序列的典型特征，同时自相关图呈现出明显的正弦波动规律，这是具有周期性变化规律的非平稳序列的典型特征.自相关图显示出来的两个性质和该序列时序图显示出的带长期递增趋势的周期性质是非常吻合的.

---

例3: 以北京市每年最高气温序列绘制自相关图

> acf(temp)
>

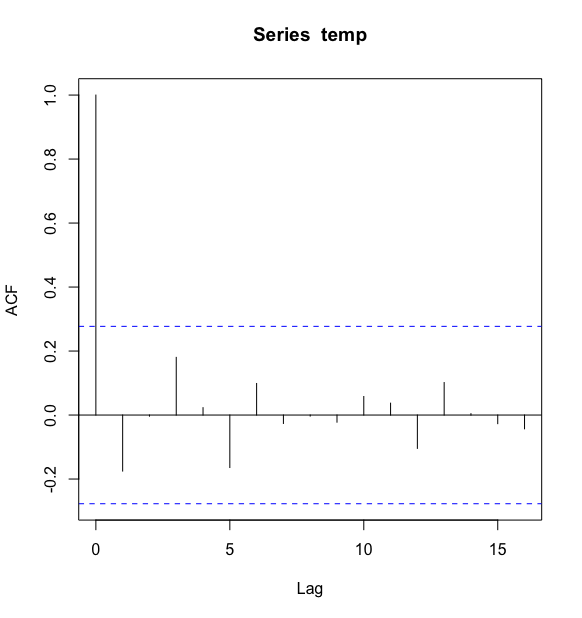
该自相关图显示该序列的自相关系数一直都比较小，始终控制在2倍的标准差范围以内，可以认为该序列自始至终都在零轴附近波动，这是随机性非常强的平稳时间序列通常具有的自相关图特征.

---

纯随机性检验

拿到一个观察值序列之后，首先是判断它的平稳性，通过平稳性检验，序列可以分为平稳性序列和非平稳序列两大类.

对于非平稳序列，由于它不具有二阶矩平稳的性质，所以对它的统计分析要费一些周折，通常要通过进一步的检验、变换或处理，才能确定适当的拟合模型.

如果序列值彼此之间没有任何相关性，那就意味着该序列是一个没有记忆的序列，过去的行为对将来的发展没有丝毫影响，这种序列称为纯随机序列.从统计分析的角度而言，纯随机序列是没有任何分析价值的序列.

纯随机序列的定义

如果时间序列 $\{X_t\}$满足如下性质:

1. 任取 $t \in T$，有 $E(X_t) = \mu$

2. 任取 $t,s \in T$，有

   $$\gamma(t,s) = \begin{cases} \sigma^2 , t = s \\ 0\ \ , t \neq s \end{cases}$$ 称序列 $\{X_t\}$为纯随机序列，也称为白噪声(white noise)序列，简记为 $X_t \approx W N(\mu,\sigma^2)$

之所以称为白噪声序列，是因为人们最初发现白光具有这种特性

例: 生成白噪声序列

#生成随机正态分布数据
> white_noise <- rnorm(1000)

#生成时间序列对象
> white_noise <- ts(white_noise)

#画出白噪声时序图
> plot(white_noise)
> 

---

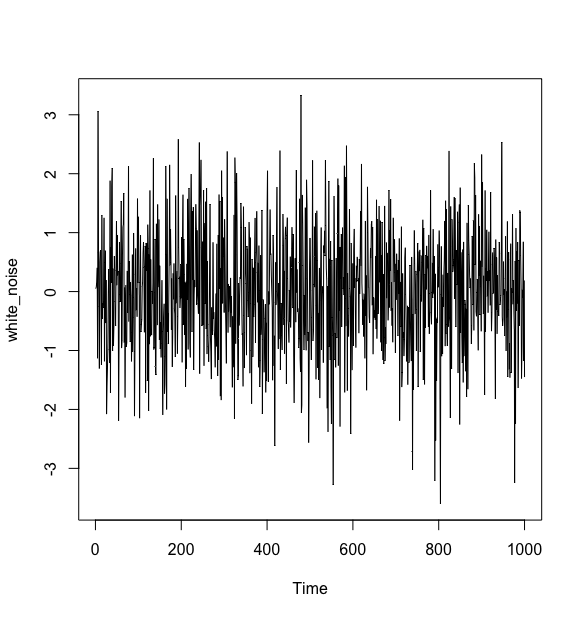
白噪声序列的性质

白噪声序列虽然简单，但是在时间序列分析中占有重要的作用

纯随机性

由于白噪声序列具有如下性质:

$$\gamma(k) = 0, \forall k \neq 0$$ 这说明白噪声序列的各项之间没有任何相关关系，这种"没有记忆"的序列就是纯随机序列.

纯随机序列各项之间没有任何关联，序列在进行完全无序的随机波动.一旦某个随机事件呈现出纯随机波动的特征，就认为该随机事件没有包含任何值得提取的有用信息，我们就应该终止分析.

一旦观察值序列中蕴含的相关信息完全提取出来了，那么剩下的残差序列就应该呈现出纯随机序列的性质.所以纯随机性还是判断相关信息是否被充分提取的一个判断标准.

---

方差齐性

所谓方差齐性，就是指序列中每个变量的方差都相等，即

$$D(X_t) = \gamma(0) = \sigma^2$$ 如果序列不满足方差齐性，就称该序列具有异方差性.

在时间序列分析中，方差齐性是一个非常重要的限制条件，因为根据马尔科夫定理，只有方差齐性假定成立，我们用最小二乘法得到的未知参数估计值才是准确、有效的.如果假定不成立，最小二乘估计值就不是方差最小线性无偏估计，拟合模型的精度会受到很大影响.

所以我们在进行模型拟合时，检验内容之一就是要检验拟合模型的残差是否满足方差齐性假定.如果不满足，那就说明残差序列还不是白噪声序列，即拟合模型没有充分提取随机序列中的相关信息，这时拟合模型的精度是值得怀疑的.在这种场合下，我们通常需要使用适当的条件异方差模型来处理异方差信息.

---

纯随机性检验

纯随机性检验也称为白噪声检验，是专门用来检验序列是否为纯随机序列的一种方法.我们知道如果一个序列是纯随机序列，那么它的序列值之间应该没有任何相关关系，即满足

$$\gamma(k) = 0, \forall k \neq 0$$ 这是一种理论上才会出现的理想状况，实际上，由于观察值序列的有限性，导致纯随机序列的样本自相关系数不会绝对为零.

例如: 白噪声序列的样本自相关图

> acf(white_noise)
>

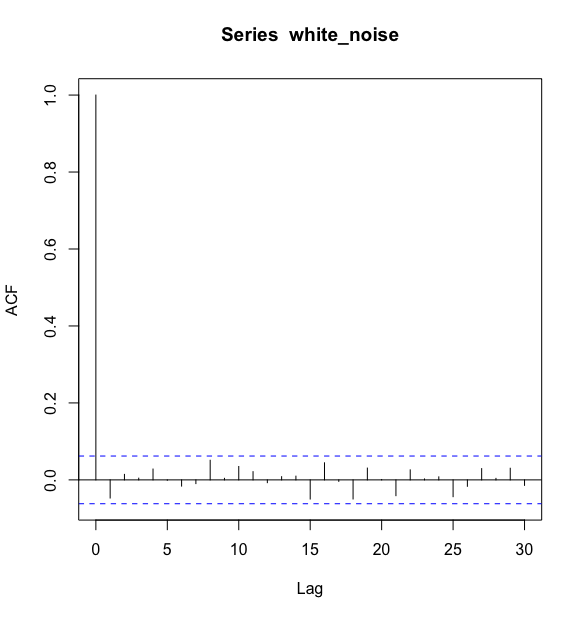
样本自相关图显示这个纯随机序列没有一个样本自相关系数严格等于零.但这些自相关系数确实都非常小，都在零值附近以一个很小的幅度随机波动.这就提醒我们应该考虑样本自相关系数的分布性质，从统计意义上来判断序列的纯随机性质.

Barlett证明，如果一个时间序列是纯随机的，得到一个观察期数为 $n$ 的观察序列$\{x_t, t = 1,2,\cdots,n\}$，那么该序列的延迟非零期的样本自相关系数将近似服从均值为零、方差为序列观察期数倒数的正态分布，即

$$\hat{\rho}_k \approx N\left(0, \frac{1}{n} \right), \forall k \neq 0$$ 式中，$n$为序列观察期数.根据这个定理，我们可以构造检验统计量来检验序列的纯随机性质.

假设条件

1. 原假设: 延迟期数小于或等于 $m$ 期的序列值之间相互独立.

2. 备择假设: 延迟期数小于或等于 $m$期的序列值之间有相关性.

该假设条件用数学语言描述为:

$$H_0 : \rho_1 = \rho_2 = \cdots = \rho_m = 0, \forall m \geq 1 \\ H_1 : 至少存在某个 \rho_k \neq 0 , \forall m \geq 1, k \leq m$$

检验统计量

$Q$统计量

为了检验这个联合假设，Box和Pierce推导出了 $Q$统计量:

$$Q = n\sum_{k=1}^m{\hat{\rho}_k^2}$$ 式中，$n$为序列观察期数；$m$为指定延迟期数.

根据正态分布和卡方分布之间的关系，我们很容易推导出 $Q$统计量近似服从自由度为 $m$的卡方分布:

$$Q = n \sum_{k=1}^m {\hat{\rho}_k^2} \approx \chi^2(m)$$ 当 $Q$统计量大于 $\chi_{1-\alpha}^2(m)$分位点，或该统计量的 $P值$小于 $\alpha$时，则可以以 $1-\alpha$的置信水平拒绝原假设，认为该序列为非白噪声序列；否则，接受原假设，认为该序列为纯随机序列.

---

LB统计量

在实际应用中人们发现 $Q$统计量在大样本场合(n 很大的场合)检验效果很好，但是在小样本场合不太精确.为了弥补这一缺陷，Box和Ljung又推导出了 $LB(Ljung-Box)统计量$:

$$LB = n(n+2)\sum_{k=1}^m{\left( \frac{\hat{\rho}_k^2}{n-k} \right)}$$ 式中，$n$为序列观察期数；$m$为指定延迟期数.

Box和Ljung证明$LB统计量$同样近似服从自由度为$m$卡方分布.

例: 计算白噪声序列延迟6期、延迟12期的 $Q_{LB}统计量$的值，并判断该序列的随机性$(\alpha = 0.05)$

#延迟6期纯随机性检验
> Box.test(white_noise, lag = 6)

    Box-Pierce test

data:  white_noise
X-squared = 3.4973, df = 6, p-value = 0.7443

#延迟12期纯随机性检验
> Box.test(white_noise, lag = 12)

    Box-Pierce test

data:  white_noise
X-squared = 7.9242, df = 12, p-value = 0.791

>

由于$P值$显著大于显著性水平 $\alpha$，所以该序列不能拒绝纯随机的原假设.换言之，我们可以认为该序列的波动没有任何统计规律可循，因而可以停止对该序列的统计分析.

平稳序列通常具有短期相关性，如果序列值之间存在显著的相关关系，通常只存在于延迟期数比较短的序列值之间.所以没必要进行长期延迟期数的计算.