机器学习篇

极大似然估计

之前看很多机器学习中估计参数都是用的极大似然估计，一般只是大概了解，这里专门调研了下，汇总一下。

贝叶斯决策

先给出经典的贝叶斯公式:

$$p(y|x) = \frac{p(x|y)p(y)}{p(x)}$$
其中:
$p(y)$ 为先验概率，表示每种类别分布的概率；
$p(x|y)$ 类条件概率，表示在某种类别的前提下，某事发生的概率；
$p(y|x)$ 为后验概率，表示某事发生了，并且它属于某一类别的概率，有了这个后验概率，我们就可以对样本进行分类.

后验概率越大，说明某事物属于这个类别的可能性越大，我们越有理由把它归到这个类别下.

---

先看一个例子: 假设在夏季，某公园男性穿凉鞋的概率为 $\frac{1}{2}$ ，女性穿凉鞋的概率为 $\frac{2}{3}$，并且该公园中男女比例通常是 $2:1$。

问题: 若你在公园中随机遇到一个穿凉鞋的人，请问他的性别为男性或女性的概率分别为多少？

从问题看，某事发生了，它属于某一类别的概率是多少？即后验概率。

设: $y_1$ = 男性，$y_2$ = 女性，$x$ = 穿凉鞋.

整理已知条件得: 先验概率 $p(y_1) = \frac{2}{3}, p(y_2) = \frac{1}{3}$
类条件概率 $p(x|y_1) = \frac{1}{2},p(x|y_2) = \frac{2}{3}$

男性和女性穿凉鞋相互独立，所以:

$$p(x) = p(x|y_1)p(y_1) + p(x|y_2)p(y_2) = \frac{5}{9}$$

则由贝叶斯公式算出:

$$\begin{array} & p(y_1|x) = \frac{p(x|y_1)p(y_1)}{p(x)} = \frac{\frac{1}{2}*\frac{2}{3}}{\frac{5}{9}} = \frac{3}{5} \\ p(y_2|x) = \frac{p(x|y_2)p(y_2)}{p(x)} = \frac{\frac{2}{3}*\frac{1}{3}}{\frac{5}{9}} = \frac{2}{5} \end{array}$$

---

极大似然估计

概述

在实际问题中，往往我们能获得的数据可能只有有限数目的样本数据，而先验概率 $p(y_i)$ 和类条件概率（各类的总体分布）$p(x|y_i)$ 都是未知的。

根据仅有的样本数据进行分类时，一种可行的办法是我们需要先对先验概率和类条件概率进行估计，然后再套用贝叶斯分类器.

类条件概率的估计很难，原因包括：概率密度函数包含一个随机变量的全部信息；样本数据可能不多；特征向量 $x$ 的维度可能很大等等。总之要直接估计类条件概率的密度函数很难。

解决办法就是：假设我们是全知全能的神，知道了样本和类别的概率分布形式，就可以把估计完全未知的概率密度 $p(x|y_i)$ 转化为估计参数。这里就将概率密度估计问题转化为参数估计问题，极大似然估计就是一种参数估计方法。

当然了，概率密度函数的选取很重要，模型正确，在样本区域无穷时，我们会得到较准确的估计值，如果模型都错了，那估计半天的参数，肯定也没有什么意义.

---

原理

参数估计问题只是实际问题求解过程中的一种简化方法，由于直接估计类条件概率函数很困难，所以能够使用极大似然估计方法的样本必须满足一些前提条件。

重要前提：训练样本的分布能代表样本的真实分布，每个样本集中的样本都是所谓独立同分布的随机变量，且有充分的训练样本。

---

极大似然估计的原理，用一张图片来说明，如下:

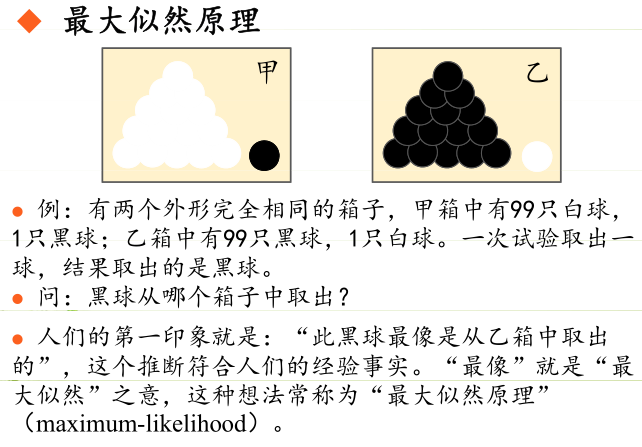
总结来说，最大似然估计的目的是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

由于样本集中的都是独立同分布的，可以只考虑一类样本集 $D$，来估计参数向量 $\theta$。

记已知的样本集为:

$$D = \{ x_1,x_2,\cdots,x_N \}$$
似然函数（linkehood function）: 联合概率密度函数 $p(D|\theta)$ 称为相对于 $\{x_1,x_2,\cdots,x_N\}$ 的 $\theta$ 的似然函数。

$$l(\theta) = p(D|\theta) = p(x_1,x_2,\cdots,x_N|\theta) = \prod_{i=1}^N p(x_i|\theta)$$

如果 $\hat{\theta}$ 是参数空间中能使似然函数 $l(\theta)$ 最大的 $\theta$ 值，则 $\hat{\theta}$ 应该是“最可能”的参数值，那么 $\hat{\theta}$ 就是 $\theta$ 的极大似然估计值。

---

ML 估计：求使得出现该组样本的概率最大的 $\theta$ 值:

$$\hat{\theta} = arg \ \max_{\theta} l(\theta) = arg \ \max_{\theta} \prod_{i=1}^N p(x_i|\theta)$$

为了便于分析，定义对数似然函数，将乘法变成加法:

$$H(\theta) = \ln\;{l(\theta)}$$
于是目标函数就可以改写成: $$\hat{\theta} = arg \ \max_{\theta} H(\theta) = arg \ \max_{\theta} \ln\;{l(\theta)} = arg \ \max_{\theta} \sum_{i=1}^N \ln{p(x_i|\theta)}$$

• 未知参数只有一个（$\theta$ 为标量）

在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解:

$$\frac{dH(\theta)}{d \theta} = \frac{d \ln{l(\theta)}}{d \theta} = 0$$

• 未知参数有多个（$\theta$ 为向量）

则 $\theta$ 可表示为具有 $S$ 个分量的未知向量:

$$\theta = [\theta_1,\theta_2,\cdots,\theta_S]^T$$

记梯度算子:

$$\nabla_{\theta} = \left[ \frac{\partial}{\partial \theta_1},\frac{\partial}{\partial \theta_2},\cdots,\frac{\partial}{\partial \theta_S} \right]^T$$

若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解:

$$\nabla_{\theta}H(\theta) = \nabla_{\theta} \ln{l(\theta)} = \sum_{i=1}^N \nabla_{\theta} \ln{p(x_i | \theta)} = 0$$

方程的解只是一个估计值，只有在样本数趋于无限多的时候，它才会接近真实值.

---

例子

上面的原理中，我们没有给出具体的概率分布形式，在这个例子中，我们假设样本服从正态分布 $N(\mu,\sigma^2)$，则似然函数为:

$$L(\mu,\sigma^2) = \prod_{i=1}^N \frac{1}{\sqrt{2\pi}\sigma} e^{\frac{(x_i - \mu)^2}{2\sigma^2}} = (2\pi\sigma^2)^{-\frac{n}{2}}e^{-\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i - \mu)^2}$$

它的对数式为:

$$\ln{L(\mu,\sigma^2)} = -\frac{n}{2} \ln{(2\pi)} - \frac{n}{2}\ln{\sigma^2} - \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2$$

分别对 $\mu,\sigma$ 求偏导得:

$$\begin{cases} \frac{\partial \;ln{L(\mu,\sigma^2)}}{\partial \mu} = \frac{1}{\sigma^2} \sum_{i=1}^n(x_i - \mu) = 0 \\ \frac{\partial \;ln{L(\mu,\sigma^2)}}{\partial \sigma^2} = -\frac{n}{2\sigma^2} + \frac{1}{2 \sigma^4} \sum_{i=1}^n(x_i - \mu)^2 = 0 \end{cases}$$

联合解得:

$$\begin{cases} \mu^* = \overline{x} = \frac{1}{n} \sum_{i=1}^n x_i \\ \sigma^{*2} = \frac{1}{n} \sum_{i=1}^n (x_i - \overline{x})^2 \end{cases}$$

似然方程有唯一解 $(\mu^*,\sigma^{*2})$；而且它一定是最大值点，这是因为当 $|\mu| \rightarrow \infty$ 或 $\sigma^2 \rightarrow \infty 或 0$ 时，非负函数 $L(\mu,\sigma^2) \rightarrow 0$ 。于是 $\mu,\sigma^2$ 的极大似然估计为 $(\mu^*,\sigma^{*2})$ .

---

R 程序演示

library(MASS)
geyser
attach(geyser)
geyser
hist(waiting)
LL <- function(params,data){
  #params: p,mu1,sigma1,mu2,sigma2
  #data: 观测数据
  t1 <- dnorm(data,params[2],params[3])
  t2 <- dnorm(data,params[4],params[5])
  #混合密度函数
  f <- params[1]*t1 + (1-params[1])*t2
  ll <- sum(log(f))
  #log-likelihood 函数
  return(-ll)
}
hist(waiting,freq = F)
lines(density(waiting))
geyser.res <- nlminb(c(0.5,50,10,80,10),LL,data = waiting,
                     lower = c(0.0001,-Inf,0.0001,-Inf,-Inf,0.0001),
                     upper = c(0.999,Inf,Inf,Inf,Inf))
geyser.res$par
X <- seq(40,120,length = 100)
p <- geyser.res$par[1]
mu1 <- geyser.res$par[2]
sig1 <- geyser.res$par[3]
mu2 <- geyser.res$par[4]
sig2 <- geyser.res$par[5]
f <- p*dnorm(X,mu1,sig1) + (1-p)*dnorm(X,mu2,sig2)
hist(waiting,probability = T,col = 0,ylab = "Density",ylim = c(0,0.04),xlab = "Eruption waiting times")
lines(X,f)

参考

• https://www.zhihu.com/question/20447622
• http://blog.csdn.net/zengxiantao1994/article/details/72787849