Week03. Statistics with R Part01

Coursera 2018.01

Defining Probability

1. Introduction

• random process

  In a random process we know what outcomes could happen, but we don't know which particular outcome will happen.

• probability

  • $P(A)$ = probability of event A

  • There are several possible interpretations of probability but they (almost) completely agree on the mathematical rules probability must follow:
    

    $$0 \le P(A) \le 1$$

• frequentist interpretation

  The probability of an outcome is the proportion of times the outcome would occur if we observed the random process an infinite number of times.

• bayesian interpretation

  • A Bayesian interprets probability as a subjective degree of belief.

  • Largely popularized by revolutionary advance in computational technology and methods during the last twenty years.

• law of large numbers

  die n.骰子

  • 大数定律
    law of large numbers states that as more observations are collected, the proportion of occurrences with a particular outcome converges to the probability of that outcome.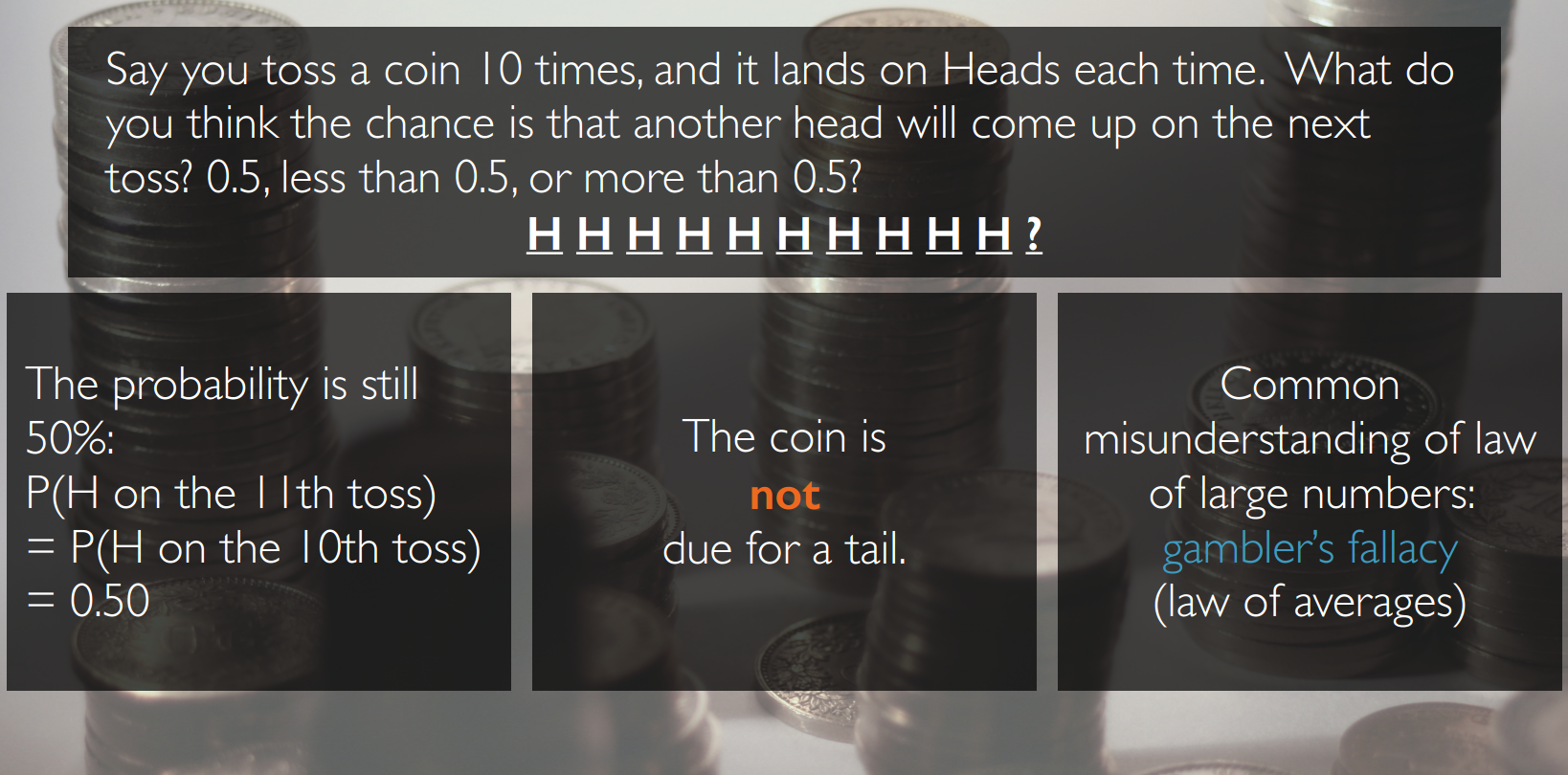

    

  • 赌徒谬论
    The common misunderstanding of the law of large numbers is that random processes are supposed to compensate for whatever happened in the past. This is called the gambler's fallacy, or the law of averages.

2. disjoint events + general addition rule

• disjoint (mutually exclusive)

  互斥事件

  • disjoint (mutually exclusive) events cannot happen at the same time.

    • the outcome of a single coin toss cannot be a head and a tail.

    • a student con't both fail and pass a class.

    • a single card drawn from a deck cannot be an ace and a queen

  • non-disjoint events can happen at the same time

    • a student can get an A in Stats and A in Econ in the same semester

  

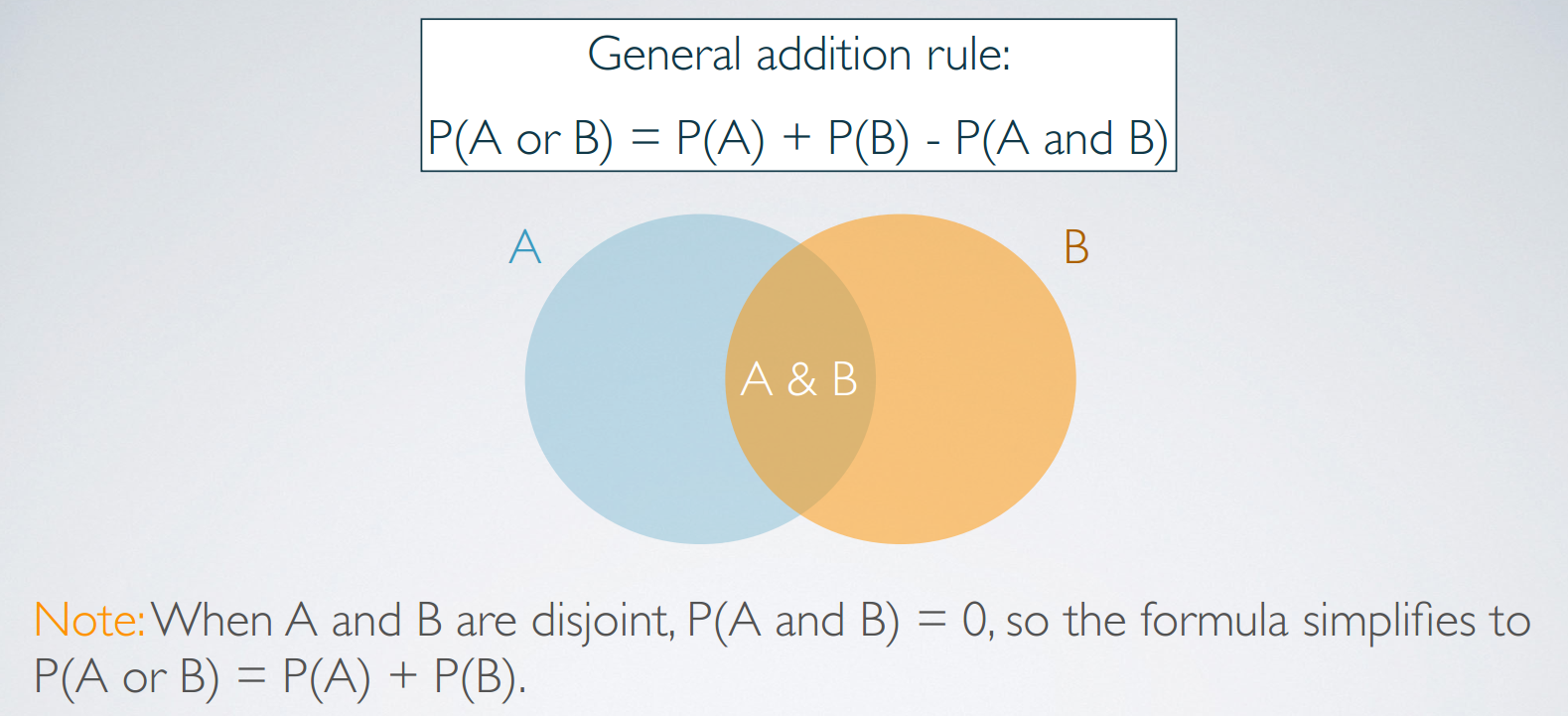
• union of disjoint events

  互斥事件的组合

  For disjoint events $A$ and $B$,
  

  $$P(A \ or \ B) = P(A) + P(B)$$

• union of non-disjoint events

  For non-disjoint events $A$ and $B$,
  

  $$P(A \ or \ B) = P(A) + P(B) - P(A \ and \ B)$$

• general addition rule

  

• sample space

  a sample space is a collection of all possible outcomes of a trial

  

• probability distributions
  概率分布

  • a probability distribution lists all possible outcomes in the sample space, and the probabilities with which they occur.

  • rules

    1. the events listed must be disjoint
    2. each probability must be between 0 and 1
    3. the probabilities must total 1

    

• complementary events
  互补事件

  complementary events are two mutually exclusive events whose probabilities add up to 1.

  

• disjoint vs. complementary

  

3. independence

• independence

  two processes are independent if knowing the outcome of one provides no useful information about the outcome of the other.

  

• checking for independence:

  $P(A | B) = P(A)$, then $A$ and $B$ are independent.

• practice

  

• determining dependence based on sample data

  

• Product rule for independent events:

  If $A$ and $B$ are independent, $P(A and B) = P(A) \times P(B)$

  

4. probability example

见课件pdf吧.

5. disjoint vs. independent

一枚硬币，抛一次，正面朝上和反面朝上是互斥但相关的事件；
抛两次，两次的结果之间是不相关的。

Defining Probability

条件概率

1. conditional probability

• study

  

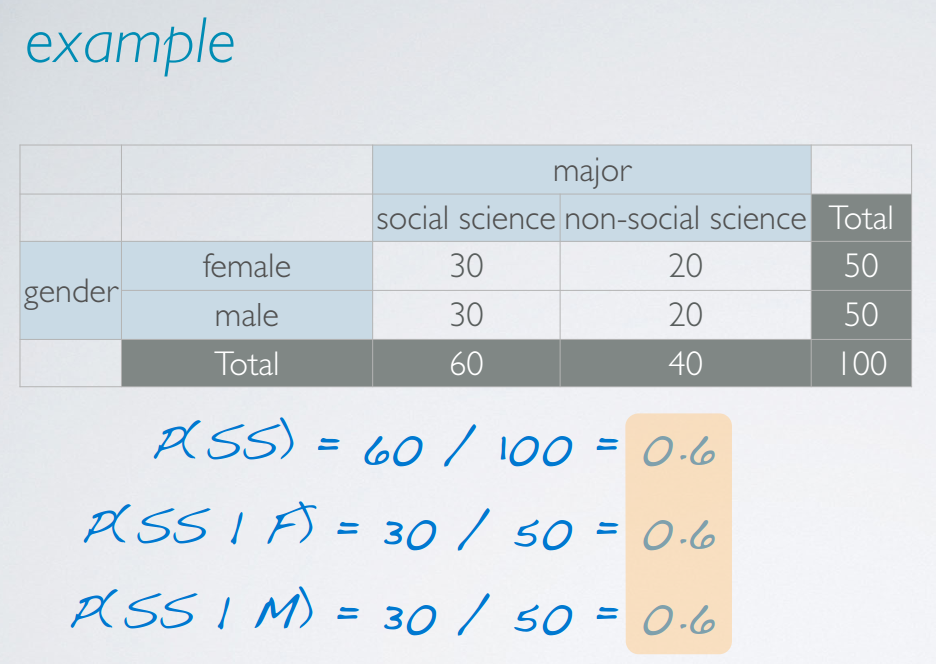
• marginal

  

  边缘概率，因为在contingency table的边缘。

• joint

  联合概率，关键词是and

  

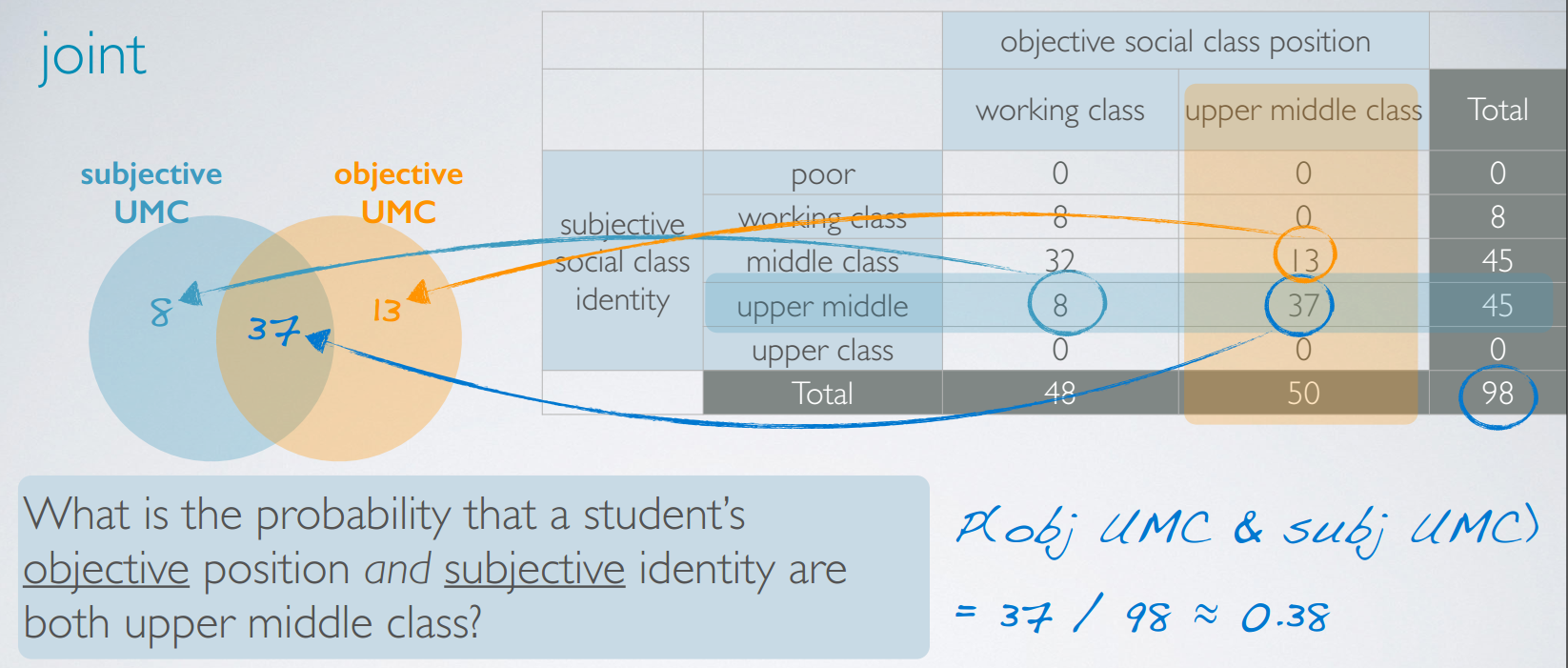
• conditional

  条件概率

  

  • 利用贝叶斯定理(Bayes' theorem)来计算

    

• Product rule for independent events:

  If $A$ and $B$ are independent, $P(A \ and \ B) = P(A) \times P(B)$

  

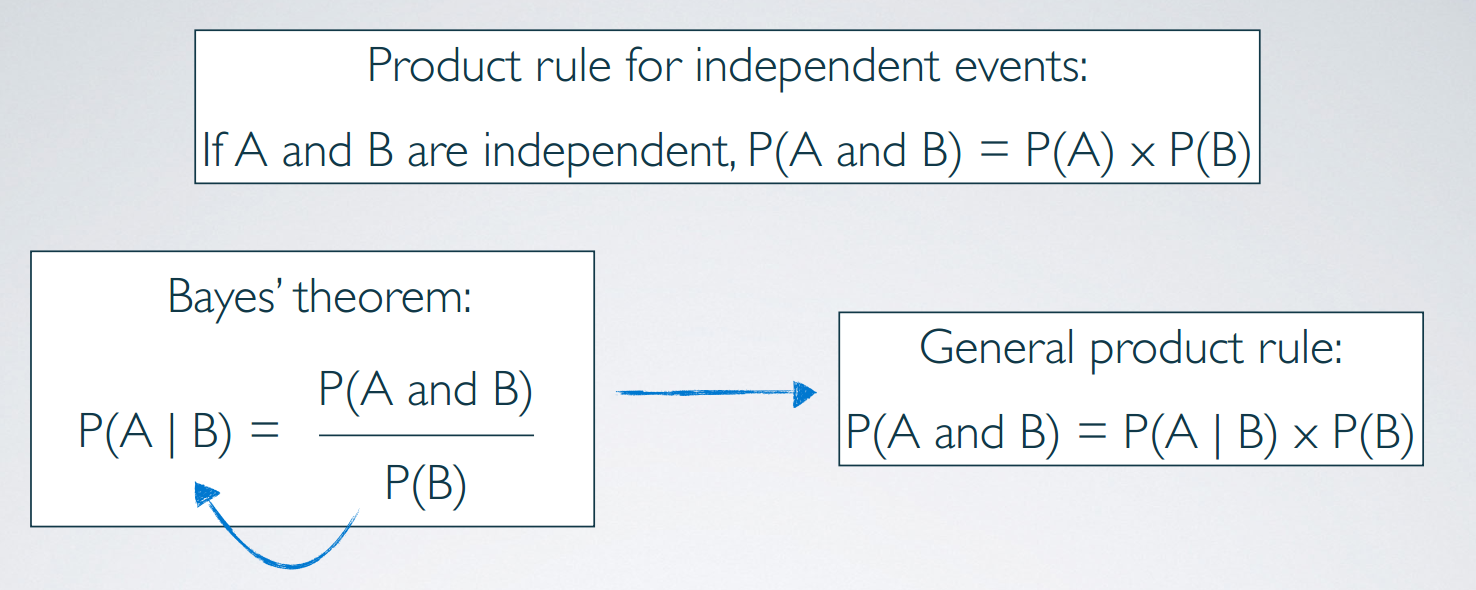
• independence and conditional probabilities

  Generically, if $P(A|B) = P(A)$ then the events A and B are said to be independent.

  • Conceptually: Giving B doesn’t tell us anything about A.

  • Mathematically: If events A and B are independent, $P(A \ and \ B) = P(A) × P(B)$. Then,
    

    $$\begin{align*} P(A | B) =\frac{P(A \ and \ B)}{P(B)}=\frac{P(A) \times P(B)}{P(B)} = P(A) \end{align*}$$

    

2. probability trees

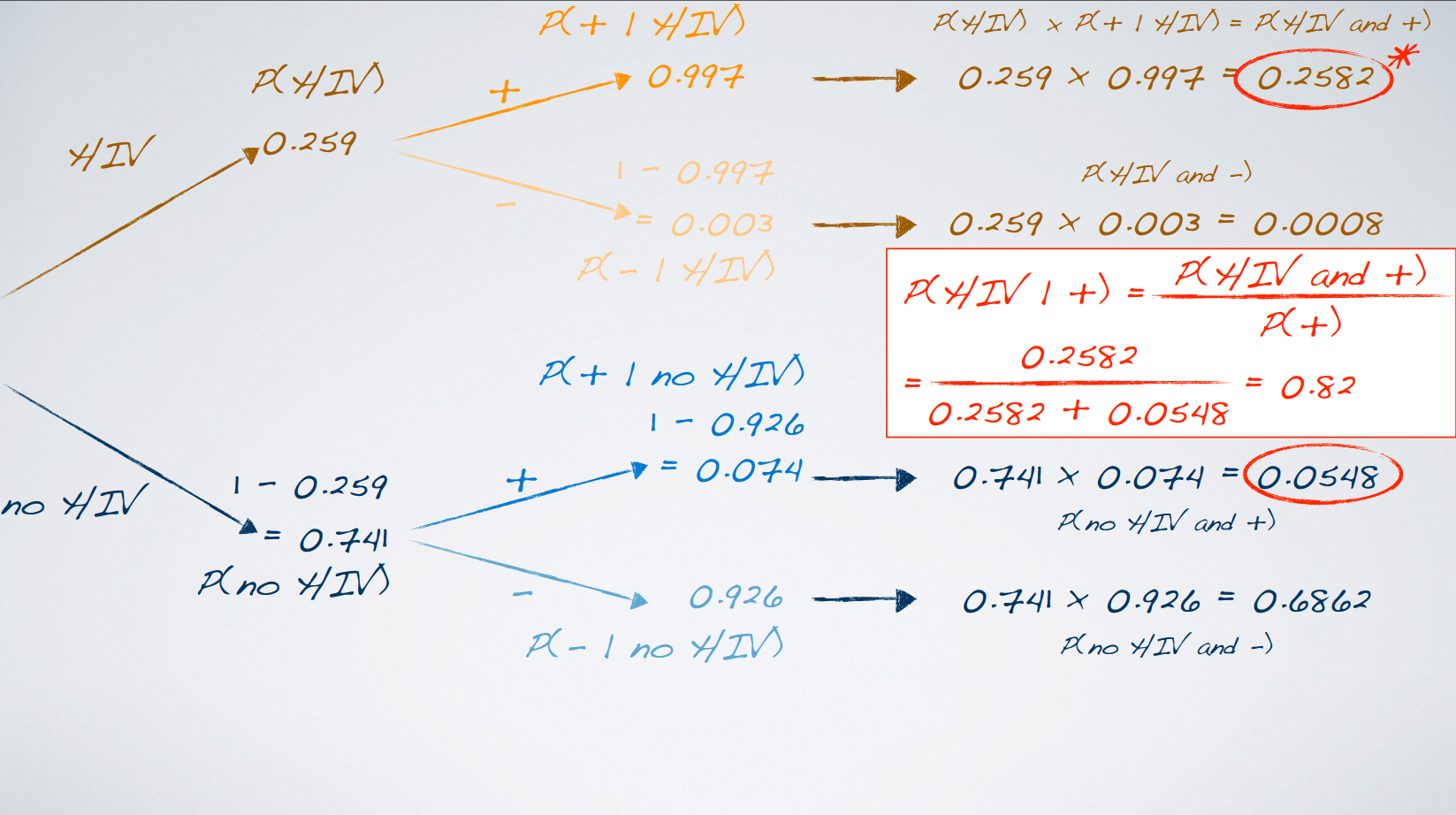
3. bayesian inference

• set-up

  

• probabilities

  

• “good die”

  

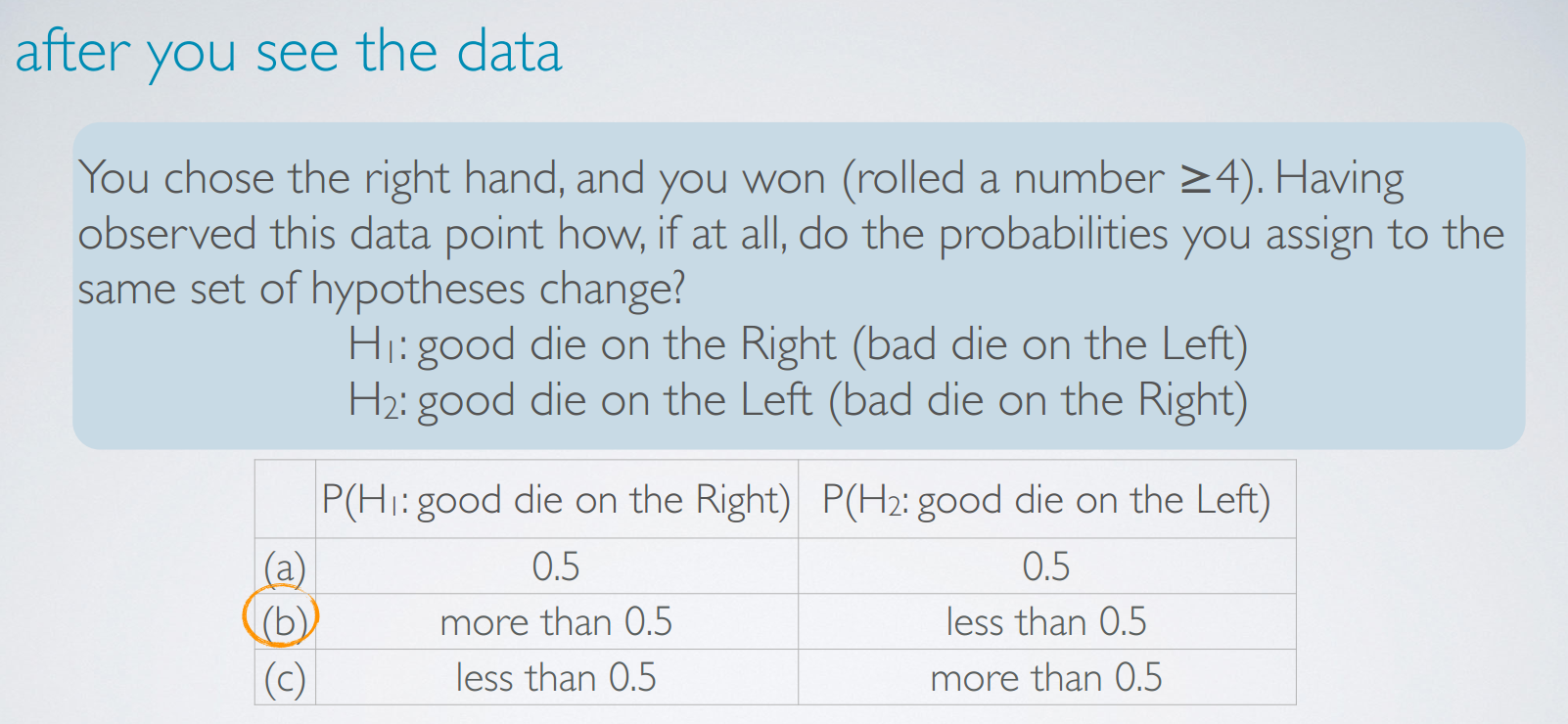
• hypotheses and decisions

  

• before you collect data

  

  prior 先验概率

• data collection: round #1

• after you see the data

  

  

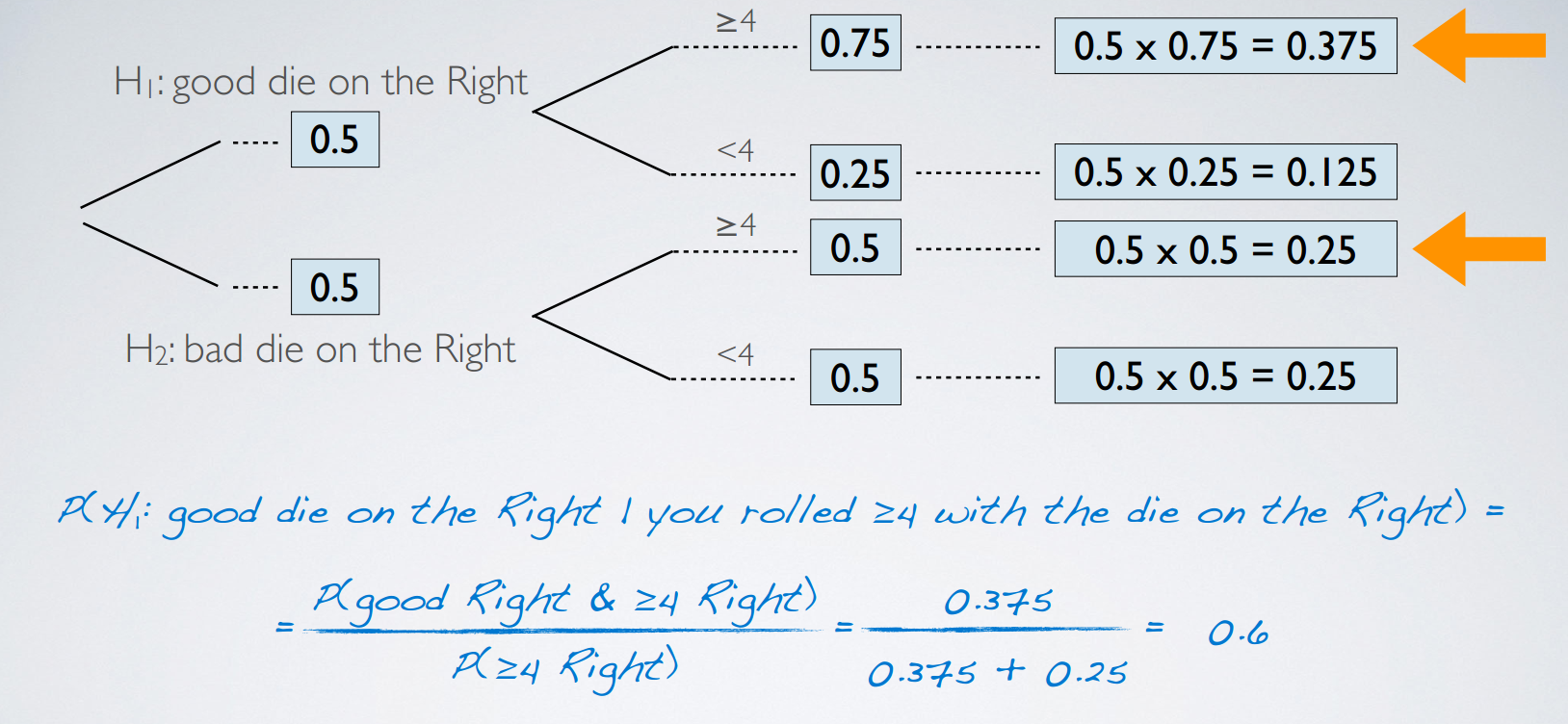
• posterior

  • The probability we just calculated is also called the posterior probability.
    

    $$P(H1: \text{good die on the Right} | \text{you rolled} \ge 4 \ \text{with the die on the Right})$$

  • Posterior probability is generally defined as $P(\text{hypothesis} | \text{data})$.

  • It tells us the probability of a hypothesis we set forth, given the data we just observed.

  • It depends on both the prior probability we set and the observed data.

  • This is different than what we calculated at the end of the randomization test on gender discrimination – the probability of observed or more extreme data given the null hypothesis being true, i.e. $P(\text{data} | \text{hypothesis})$, also called a p-value.

• updating the prior

  

• recap

  

  • 利用之前的先验信息

  • 避免了违反直觉的p-value

  • 当可以获得更多数据时，坏的先验的影响也会减小

  • 比频率模型更为灵活

4. Examples of Bayesian Inference

• breat cancer

  

  

  

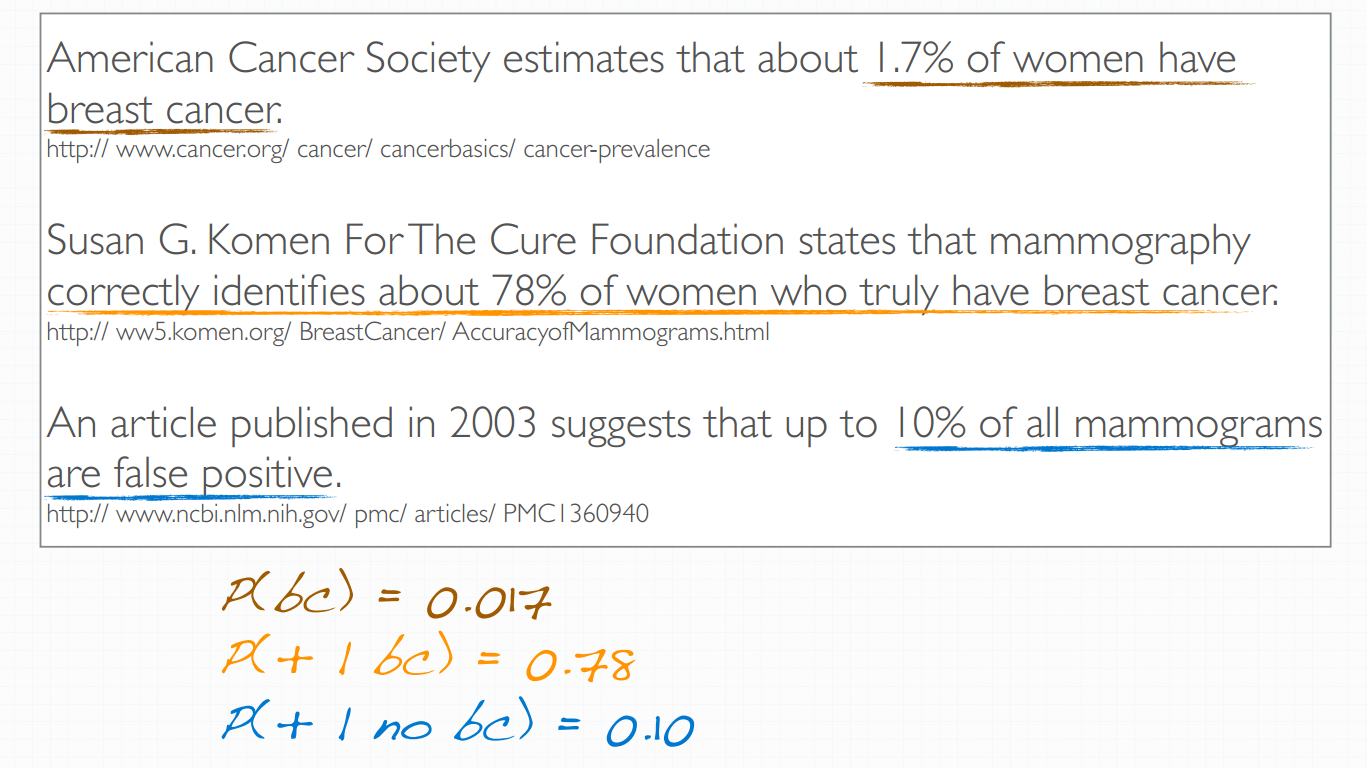
• procedure

  • setting a prior
  • collecting data
  • obtaining a posterior
  • updating the prior with the previous posterior